Mathematical Methods of Conceptual Engineering Examples

This article provides solved examples of mathematical methods of conceptual engineering including speed of sound in fluid, maximum permissible flow of water, total angle of the V belt of pulley groove, probability of having 3 components outside acceptable tolerance and more. The article also includes subject, course code, course name, professor, university, and references.

Mathematical Methods 1
MATHEMATICAL METHODS OF CONCEPTUAL ENGINEERING EXAMPLES
Name
Course
Professor
University
City/state
Date

Mathematical Methods 2
Mathematical Methods of Conceptual Engineering Examples
Task 1A
i) Prove the equation for speed of sound in any fluid
Bulk modulus, K, is given by K= −dP
( dV
v )
Where dP = change in pressure, V = initial volume and dV = change in volume (Greshnyakov &
Belenkov, 2014).
According to conservation of mass principle, density x volume = constant i.e. ρv = c
→ d(ρv) = 0; differentiating this by parts gives
ρdv + vdρ = 0
ρdV = - vdρ; collecting like terms gives
−dv
v = dρ
ρ ; substituting −dv
v in the equation for bulk modulus gives
dP
dρ = K
ρ
But dP
dρ = K
ρ
But velocity of sound, Vs= √ dP
dρ = √ K
ρ
In dimensional analysis, the units for K is N/m2 and the units for ρ is kg/m3

Mathematical Methods 3
In dimensional analysis, N = force = ML
T ² (where M = mass in kg, L = length in m and T = time
in seconds)
Thus Vs= √ K
ρ = kg∗m∗m³
s2∗m2∗kg = √ m ²
s ² =m/s
Thus Vs is i
ii) Maximum permissible flow of water
Calculate the maximum permissible flow of water in the pipeline if maximum pressure in the
pipeline is 94 x 105 N/m2 using the equation ΔP = ρVvs
units for maximum permissible flow of water through a pipe
Calculate the maximum permissible flow of water in the pipeline if maximum pressure in the
pipeline using the equation ΔP = ρVvs
According to Bernoulli equation, velocity s determined as follows:
Vs= √ 2 ΔP
ρ = √ 2 x 94 x 105 N /m2
1000 kg /m3 = 137.11 m/s
Flow rate = Vs x cross-sectional area of the pipe
Cross-sectional area of pipe = πr2 = π x (0.075m)2 = 0.01767m2
Flow rate = 137.11 m/s x 0.01767 m2 = 2.423 m3/s
how to convert m3/s into ft/s using dimensional analysis

Mathematical Methods 4
2.423 m3
s =
2.423m∗m∗m
s ∗3.2808 ft
m ∗3.2808 ft
m ∗3.2808 ft
m
¿ 2.423∗3.2808 ft∗3.2808 ft∗3.2808 ft
m =85.564 f t3 / s
Task 1C
i) Determining total angle of the “V” belt of pulley groove
T 1
T 2 =eμ θ
sin α
300 N
58.7 N =e0.2160 °
sin α → 5.1107=e0.2 160 °
sin α
Taking natural logarithm on both sides of the equation gives
Ln (5.1107) = ln (e0.2 160 °
sin α )
Ln (5.1107) =
ln ( 5.1107 ) =0.2 160 °
sin α ln(e) (but Ln e = 1)
1.6313=0.2 160 °
sin α → 1.6313
0.2 =160 °
sin α (converting 160° to radians)
8.1565=160 °
sin α → sin α= 160°
8.1565
1° = 0.0174533 radians
160° = 2.79253 radians

Mathematical Methods 5
Thus sin α= 2.79253
8.1565 =0.3424
α = Sin-1 0.3424 = 20°
Therefore total angle of the “V” belt of pulley groove is 2 x 20° = 40°
ii) Shear stress and direct stress relationship
σ =(σx−σy)
2 sin e(2 θ)
σ = 25 MN/m2, σx = 80 MN/m2 and θ = 25°
Substituting the given values in the above equation gives
25=(80−σy)
2 sin e(2 x 25)
25=(80−σy)
2 sin136°
25=(80−σy)
2 (0.6947)
(25 x 2) = (80 – σy)(0.6947) → 25 x 2
0.6947 =80−σy
71.97 = 80 – σy
σy = 80 – 71.97
σy = 8.03 MNm-2 ≈ 8 MNm-2
iii) Waveform equation

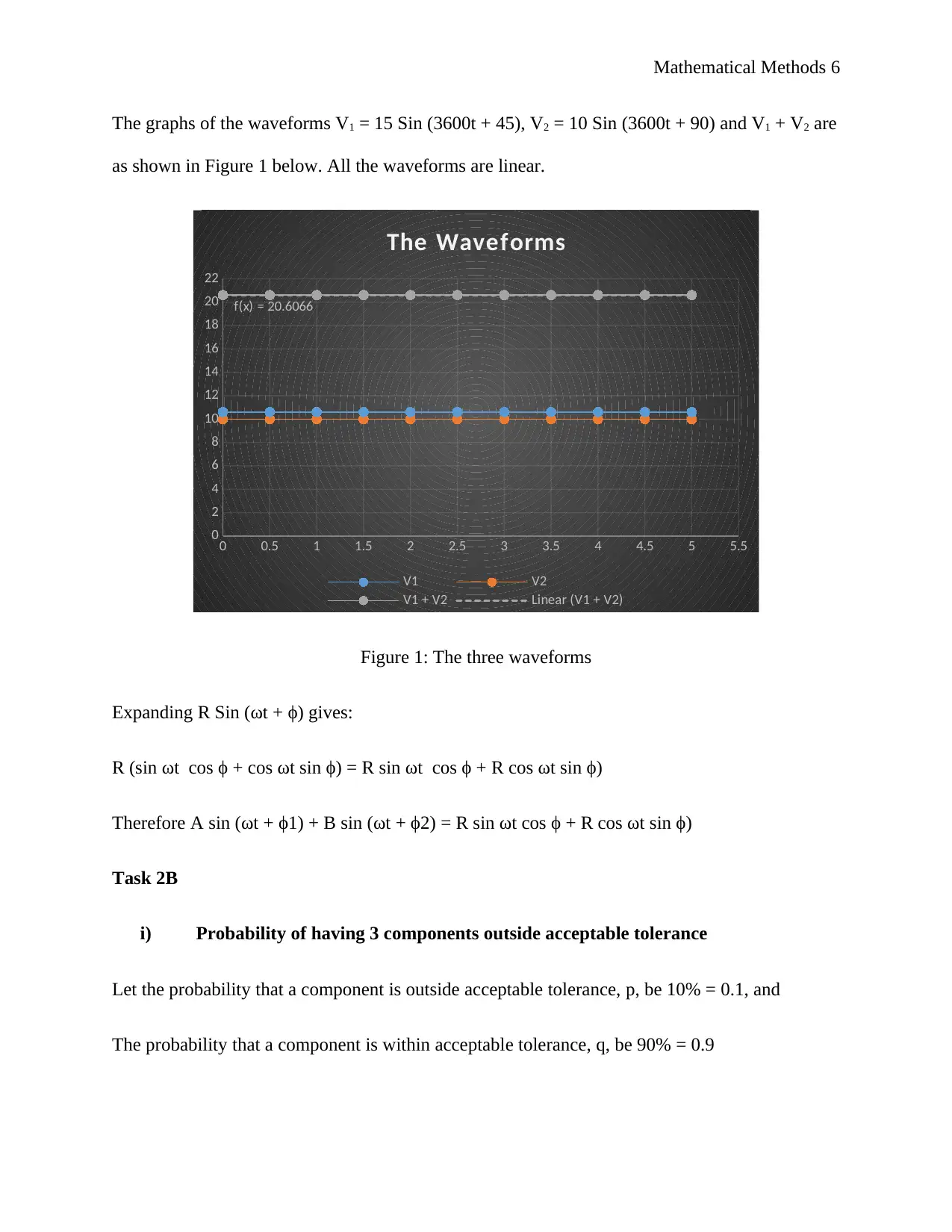
Mathematical Methods 6
The graphs of the waveforms V1 = 15 Sin (3600t + 45), V2 = 10 Sin (3600t + 90) and V1 + V2 are
as shown in Figure 1 below. All the waveforms are linear.
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 5.5
0
2
4
6
8
10
12
14
16
18
20
22
f(x) = 20.6066
The Waveforms
V1 V2
V1 + V2 Linear (V1 + V2)
Figure 1: The three waveforms
Expanding R Sin (ωt + ϕ) gives:
R (sin ωt cos ϕ + cos ωt sin ϕ) = R sin ωt cos ϕ + R cos ωt sin ϕ)
Therefore A sin (ωt + ϕ1) + B sin (ωt + ϕ2) = R sin ωt cos ϕ + R cos ωt sin ϕ)
Task 2B
i) Probability of having 3 components outside acceptable tolerance
Let the probability that a component is outside acceptable tolerance, p, be 10% = 0.1, and
The probability that a component is within acceptable tolerance, q, be 90% = 0.9

Mathematical Methods 7
Assuming binomial distribution, the probability that 0, 1, 2, 3 … components are outside
acceptable tolerance assuming binomial distribution is as follows (Bird, 2017):
(q + p)10 = (0.9 + 0.1)10 = (0.9)10 + 10(0.9)9(0.1) +
( 10 ) ( 9 )
2 ! ( 0.9 )8 ( 0.1 )2 + (10 ) ( 9 ) (8)
3! ( 0.9 )7 ( 0.1 )3 + (10 ) ( 9 ) (8)(7)
4 ! ( 0.9 )6 ( 0.1 )4 + …
Number of components outside acceptable
tolerance
Probability
0 (0.9)10
1 10(0.9)9(0.1)
2 ( 10 ) ( 9 )
2 ! ( 0.9 ) 8 ( 0.1 ) 2
3 ( 10 ) ( 9 ) (8)
3! ( 0.9 )7 ( 0.1 ) 3
4 ( 10 ) ( 9 ) (8)(7)
4 ! ( 0.9 )6 ( 0.1 )4
Etc.
Thus the probability of having 3 components that are outside of the acceptable tolerance is:
( 10 ) ( 9 ) (8)
3! ( 0.9 )7 ( 0.1 ) 3 = 120 x 0.4782969 x 0.001 = 0.057395628 = 0.0574
ii) Probability of random selection
65 capacitors = within required tolerance values
22 capacitors = below required tolerance values
13 [100 – (65 +22)] = above required tolerance values
a) Both are within required tolerance with replacement
The probability of the first capacitor selected being within the required tolerance values is 65
100

Mathematical Methods 8
After selecting the first capacitor, it is replaced meaning that the total capacitors again remain
100, hence the probability of the second capacitor selected being within the required tolerance
values is 65
100
Thus the probability of both the first and second capacitors selected being within the required
tolerance values is obtained by multiplication (Ball, 2015), as follows:
65
100 x 65
100 = 4225
10000 =0.4225
b) First one is below required tolerance values and the second one is above required
tolerance values, without replacement
The probability of the first capacitor selected being below the required tolerance values is 22
100
After selecting the first capacitor, it is not replaced hence total capacitors remaining are 99, thus
the probability of the second capacitor selected being above the required tolerance values is 13
99
Therefore the probability that the first capacitor selected being below the required tolerance and
the second one being above the required tolerance values is: 22
100 x 13
99 = 286
9900 =0.0289
References
Ball, C., 2015. Probability | Theory, solved examples and practice questions. [Online]
Available at: https://www.mbacrystalball.com/blog/2015/07/03/probability/
[Accessed 6 September 2018].
Bird, J., 2017. Engineering Mathematics. 8th ed. Abingdon, UK: Taylor & Francis.
Greshnyakov, V. & Belenkov, E., 2014. Technique for Calculating the Bulk Modulus. Russian Physics
Journal, 57(6), pp. 731-737.

Mathematical Methods 9