Mathematical Solutions - Polynomials

Solution.1
(a) 9 a4 b3−3 a3 b4
6 a3 b3−2 a2 b4
= 3 a3 b3 ( 3 a−b )
2 a2 b3 ( 3 a−b )
= 3 a3 b3 ( a−2 b−2 )
2
= 3 a
2
(b) 3 √2− √5
2 √5+ √2
= 3 √ 2− √ 5
2 √ 5+ √ 2 × 2 √ 5− √ 2
2 √ 5− √ 2
= 3 √ 2 .2 √ 5−3 √ 2 . √ 2−2 √ 5 . √ 5+ √ 5 . √ 2
20−2
= 6 √10−6−10+ √10
18
= 7 √ 10−16
18
(c) (9 x )3 / 4 x1 /3
√ 27 x3
= (9 x )1 /2 ¿ ¿
= 3 x1/ 2 ¿ ¿
= ¿ ¿
(d) 3
2 x−3 - 4
x+4 = 0
= 3 ( x + 4 ) −4 (2 x −3)
( 2 x−3 ) (x−4 )

= 3 ( x + 4 ) −4 (2 x −3)
( 2 x−3 ) (x−4 )
= 3 x +12−8 x +12
2 x2 +8 x−3 x−12
= −5 x +24
2 x2 +5 x−12
= −5 x +24
2 x ( x+ 4 )−3( x +4 )
= −5 x+ 24
(2 x−3)(x+ 4)
(e) M = w
2 (L –l2)
2M = w (L –l2)
2M = wL – wl2
wl2 = wL – 2M
l = √ L− 2 M
w
Solution.2
(a) The solution of the student is showing in the form of an equation without any
elaboration, hence it is difficult to follow. So the better way to solve the question is to
elaborate the answer step by step.
(b) Given that,
Diameter of the circle = 2 m;
Length of the rectangle = 3m;
Circumference of the circle = diameter × π
= 2 × π = 2π
Total length of the rectangle = 3+3 = 6m

So overall circumference = 2π +6
Car is driven around the track = 25 times
Hence overall covered distance = 25 (2π +6 ¿
= 25(2 ( 22
7 )+6)
= 307.14m
Solution.3
(a) y = -3x-2
Points = (-2, 4)
x = -2, y = 4
By substituting the values of x and y in the given equation;
4 = - 3(-2) – 2
4 = 6 -2
4=4
LHS = RHS
Hence the point (-2, 4) satisfies the equation y = -3x – 2.
(b) Gradient = 2
Points = (1, 8)
y = mx +c
8= 2(1) +c
C = 6
By substituting the value of c in equation;
y = 2x + 6
(c) Graph for two lines:

(d) The intersection is shown at the point in the graph, where these two lines intersect
each other.
(e) y = 2x + 6
y = -3x -2
Substituting the value of y from equation (1) in equation (2):
2x +6 = -3x -2
2x +3x = -2-6
5x = -8
x = -8/5 = -1.6
By substituting this value in equation (1);
y = 2(-1.6) +6
y= -3.2 +6
y = 2.8
Points of intersection (-1.6, 2.8)
Solution.4
(a) (i)
½ x2 -1/2 x -23/8
Dividing the whole terms by ½
x2 –x- (46/8)
x2 –x= 46/8

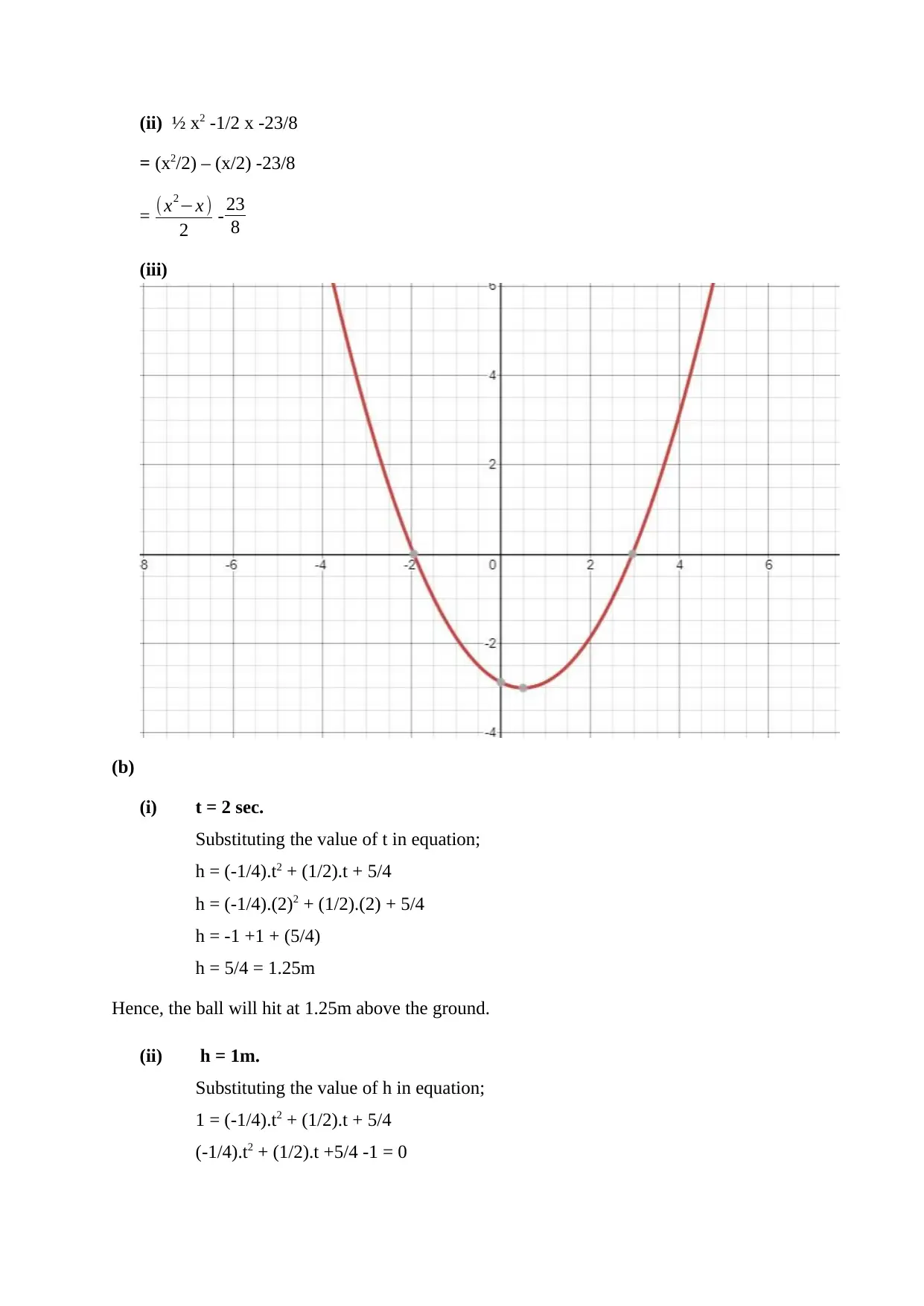
(ii) ½ x2 -1/2 x -23/8
= (x2/2) – (x/2) -23/8
= ( x2−x )
2 - 23
8
(iii)
(b)
(i) t = 2 sec.
Substituting the value of t in equation;
h = (-1/4).t2 + (1/2).t + 5/4
h = (-1/4).(2)2 + (1/2).(2) + 5/4
h = -1 +1 + (5/4)
h = 5/4 = 1.25m
Hence, the ball will hit at 1.25m above the ground.
(ii) h = 1m.
Substituting the value of h in equation;
1 = (-1/4).t2 + (1/2).t + 5/4
(-1/4).t2 + (1/2).t +5/4 -1 = 0

(-1/4).t2 + (1/2).t + (1/4) = 0
-t2 +2t +1 =0
t2 -2t -1 =0
t = (1 +√2) (1 -√2)
t = 2.41 sec.
Solution.5
(a) -2x3 +7x2 +10x -24 = 0
- (2x3 -7x2 -10x +24) = 0
2x3 -7x2 -10x +24 = 0
= (x +2) 2 x 3−7 x 2−10 x+24
( x +2)
= 2x2 + (−11 x 2−10 x +24)
(x +2)
= 2x2-11x + (12 x+24 )
(x +2)
= (x+2) (2x-3) (x-4)
(b)

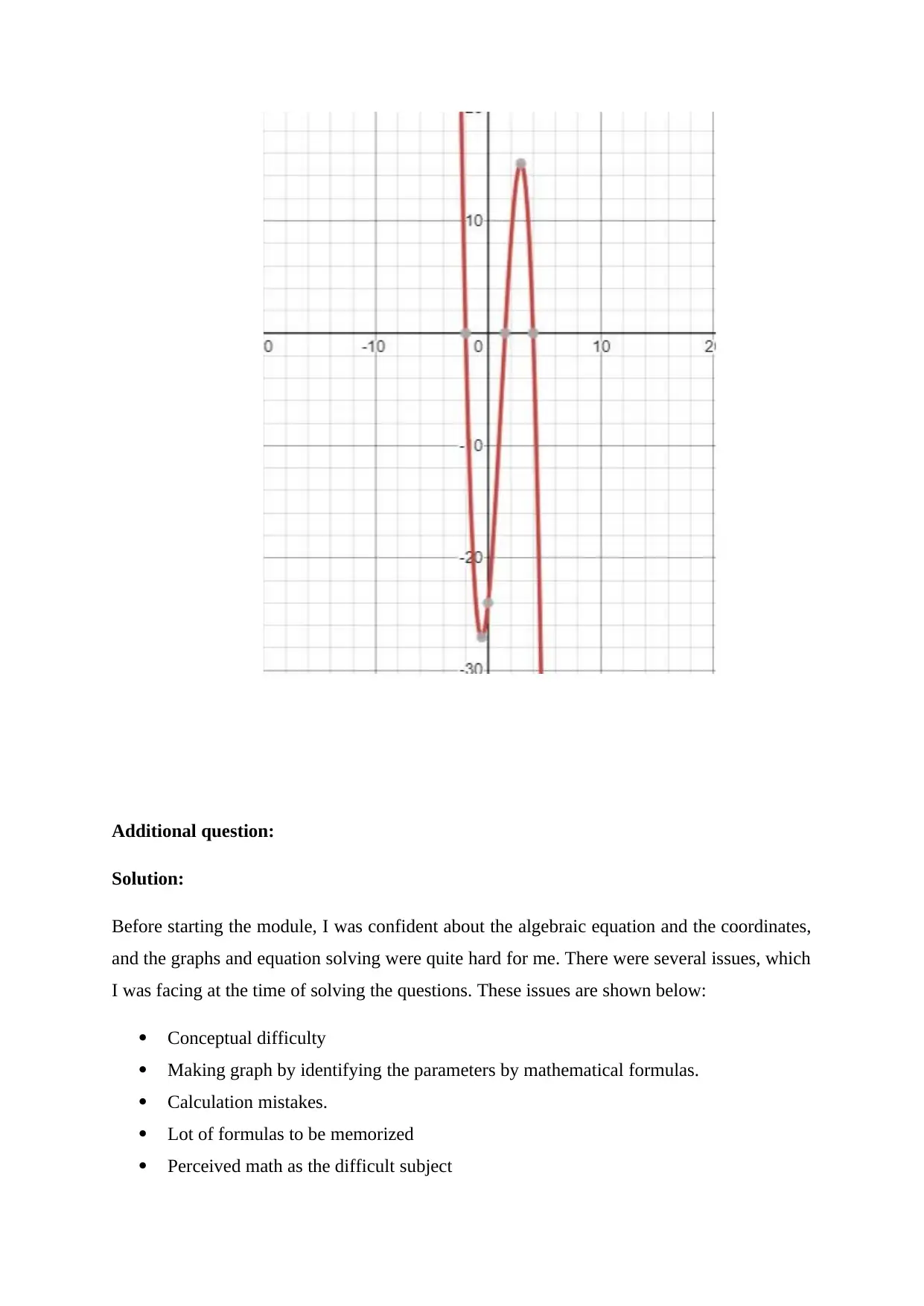
Additional question:
Solution:
Before starting the module, I was confident about the algebraic equation and the coordinates,
and the graphs and equation solving were quite hard for me. There were several issues, which
I was facing at the time of solving the questions. These issues are shown below:
 Conceptual difficulty
 Making graph by identifying the parameters by mathematical formulas.
 Calculation mistakes.
 Lot of formulas to be memorized
 Perceived math as the difficult subject

 Lot of calculations
 Lack of numerical practice.
Now after solving these questions, I am feeling really confident about these all topics. I have
found several changes in my knowledge as:
 Formulas of algebraic equation
 Location of points at the graph
 Calculation practices
 Solving procedure of quadratic expressions
 Solving process of coordinates related numerical
 Solving the geometry structure in good manner
 Making steps for numerical clarification.
Now I am feeling that I can do the question related to the algebra, geometry, coordinates and
graphs. By practicing more about these, I am also able to get the expertise on these subjects.