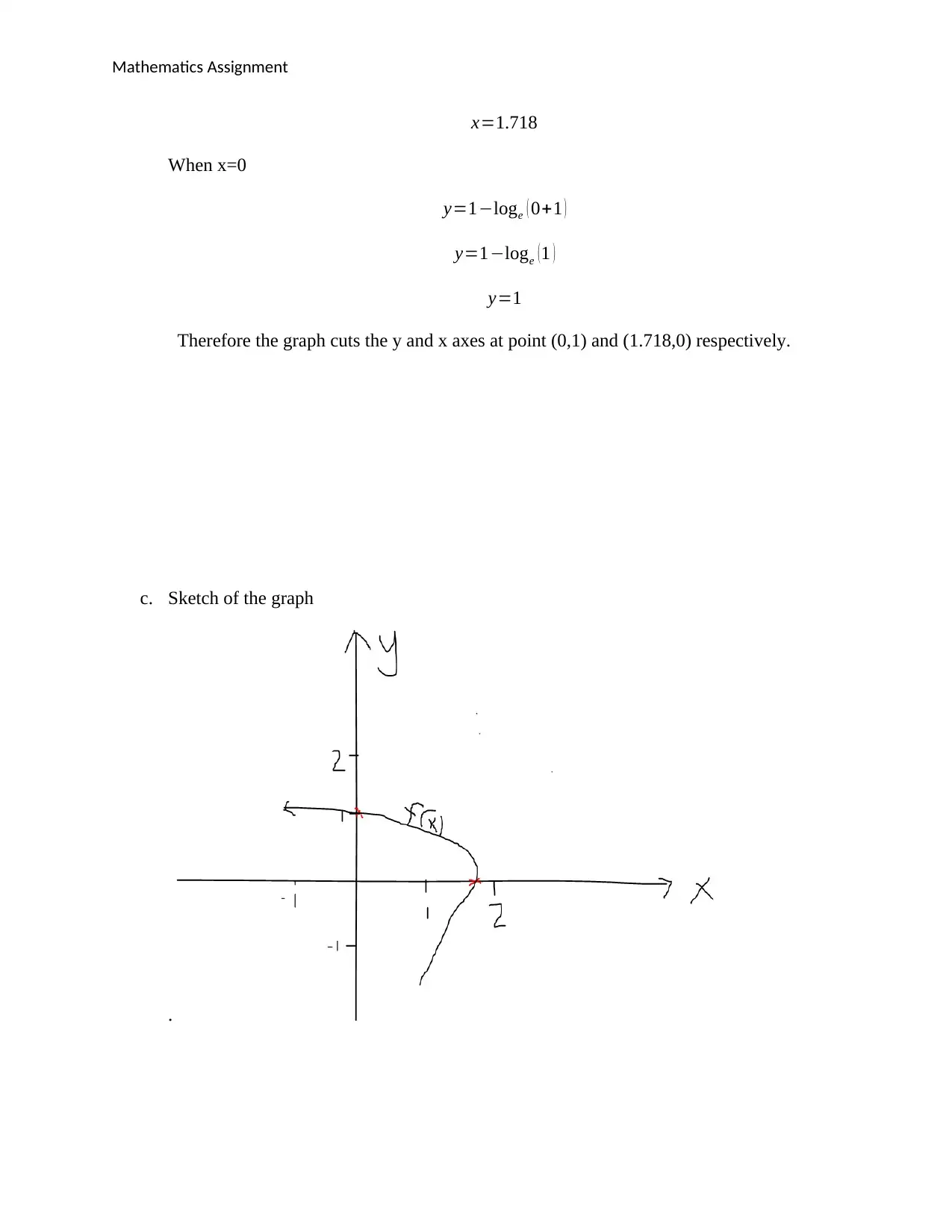
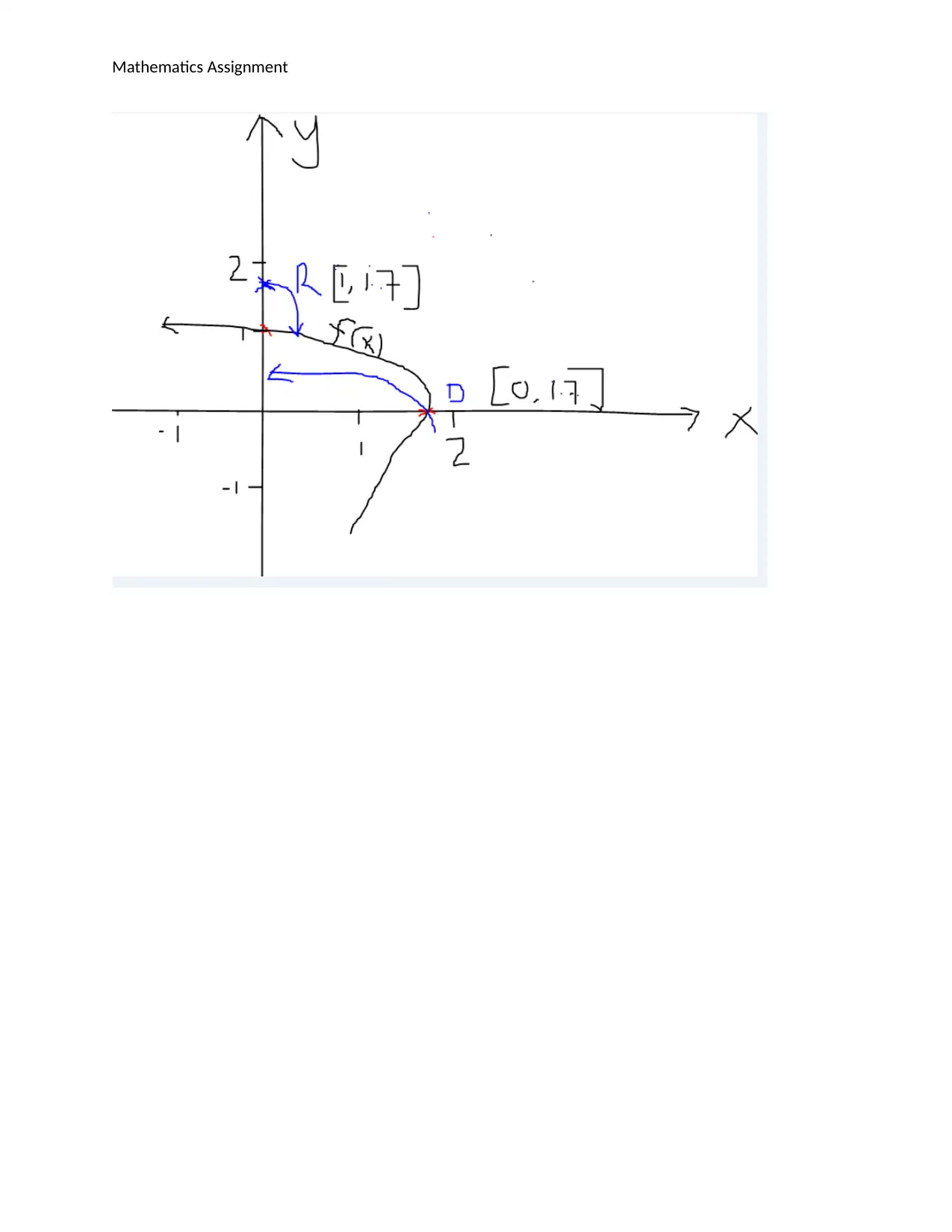
Mathematics Assignment

This Mathematics Assignment includes solutions to questions on radioactive decay, finding the smallest value of a function, sketching graphs and finding inverse functions. The subject is Mathematics and the course code and college/university are not mentioned.

Mathematics Assignment
Mathematics Assignment
Student’s Name
Institution Affiliation
Calculus

Mathematics Assignment
Question one
Radioactive Decay
The amount of decaying substance at time t is given by
A=A0 ekt , … … ..i
Given information
when t=1 , A=60.7∧when t=6 , A=5
To obtain the value of A0 ∧k , values oft∧ A, will be substituted in the equation i to
obtain two equations.
60.7=A0 ek … …ii
5=A0 e6 k … … . iii
Introduce natural logarithm
ln 60.7=ln ( A0 ek )
4.1059=ln A0 +k … …ii
ln 5=ln ( A ¿¿ 0 e6 k) ¿
1.6094=ln A0 +6 k … …iii
Below the equation obtained
4.1059=ln A0 + k … …ii

Mathematics Assignment
1.6094=ln A0 +6 k … …iii
Solve the two by elimination method
6 ( 4.1059 ) =6 ln A0 +6 k ….. ii
1.6094=ln A0 +6 k … …iii
Subtract the iii from the ii,
23.02622=5 l n A0
ln A0 =23.02622
5
ln A0 =4.6052
A0 =100.0075
A0 ≈ 100.
Substitute A0 =100.0075, in equation iii to obtain value of k
1.6094=ln ( 100.0075 ) +6 k
1.6094=4.6052+6 k
6 k =−2.9958
k =−0.4993
k ≈−0.5
Therefore, the value of A0 ∧k are A0 ≈ 100 andk ≈−0.5 respectively.

Mathematics Assignment
Question Two
The function f : [a , 4 ] →C , f ( x ) =16−x2
a. The smallest value of a such that f ( x ) is1−1 function
To find the smallest of a the derivative of f (c ) is equated to 0
0=f ' ( c ) = f ( b ) −f ( a )
b−a , where b=4∧a=a are intervals of C
0=16− ( 4 )2− (16− ( a2 ) )
4−a
¿ 0−(16−a2 )
4−a
¿ (−1 ) ( 4−a ) ( 4 +a )
4−a
0= ( −1 ) ( 4+ a )
0=4 +a
a=−4
b. Value of C
C=f [ a , b ]
when b=4 ,C=0∧when a=−4 ,C=0
Therefore, is C ≥ 0
c. Rule for the inverse of f −1

Mathematics Assignment
To do this the f (x) is change to y and then y is replaced with x and solve for y
x=16− y2
x−16= y2
y=± √ x−16
Therefore, f−1= y =± √ x−16
The domain, consideringf (x)=16−x2, value of x has greater than or equal to 4
Solve 16−x2 ≥ 0
16 ≥ x2
4 ≥ x
Therefore,
Domain [−∞ , 4 ] and range is [−∞ ,0 ]
The domain of inverse function is given by the range of original function while range is
given by domain
Thus domain and range for the inverse function are [−∞ ,0 ] and [ 4 , ∞ ] respectively.
d. Sketch graph

Mathematics Assignment
Question three
Function to be considered: f(x) = 1 − loge(x + 1)
a. Stating the transformation that have occurred to g ( x )=loge x form f(x) = 1 − loge(x +
1)
f(x) is graph of g ( x ) =loge x translated 1 unit parallel to X-axis and cut y axis
at -1
b. Coordinates where the graph cuts the x and y-axis
When y=0 and x=0
y=0
0=1−loge(x +1)
1=loge ( x +1 ) , change ¿ index form
e=x +1

Mathematics Assignment
x=1.718
When x=0
y=1−loge ( 0+1 )
y=1−loge ( 1 )
y=1
Therefore the graph cuts the y and x axes at point (0,1) and (1.718,0) respectively.
c. Sketch of the graph
.

Mathematics Assignment
d. Inverse of function
f(x) = 1 − loge(x + 1)
y=1−loge (x +1) Replace x with y and y with x and solve for y
x=1−loge ( y +1 )
x−1=−loge ( y +1 )
− ( x−1 ) =loge ( y +1 )
y +1=e− (x−1 )
y=e− (x−1 )−1
Therefore, the inverse function of y=f (x ) is
e− ( x−1 )−1
To sketch the graph, the domain and range of the inverse need to be determined.
First, determine the domain and range of y=1−loge ( x +1 ), you are interested with
1−loge ( x +1 ) ≥ 0
1 ≥ loge ( x+1 )
e ≥ x +1
1.718 ≥ x
Thus the domain and range will be [ 1 ,1.718 ] and [0, 1.718] respectively

Mathematics Assignment
They will be given by reverse of the domain and range of y=f (x ), that is
Domain: [ 0 , 1.718 ]
Range;[ 1 ,1.718 ]
Below is the sketch graph, in blue

Mathematics Assignment