Mathematics Assignment - Desklib

This Mathematics Assignment covers topics like conditional probability, independence, binomial distribution, joint and marginal pdf of continuous random variables. It also includes solved examples and graphs. The document type is an assignment and the subject is Mathematics. The course code, course name, and college/university are not mentioned.

Mathematics Assignment
Student Name:
Instructor Name:
Course Number:
2nd October 2019

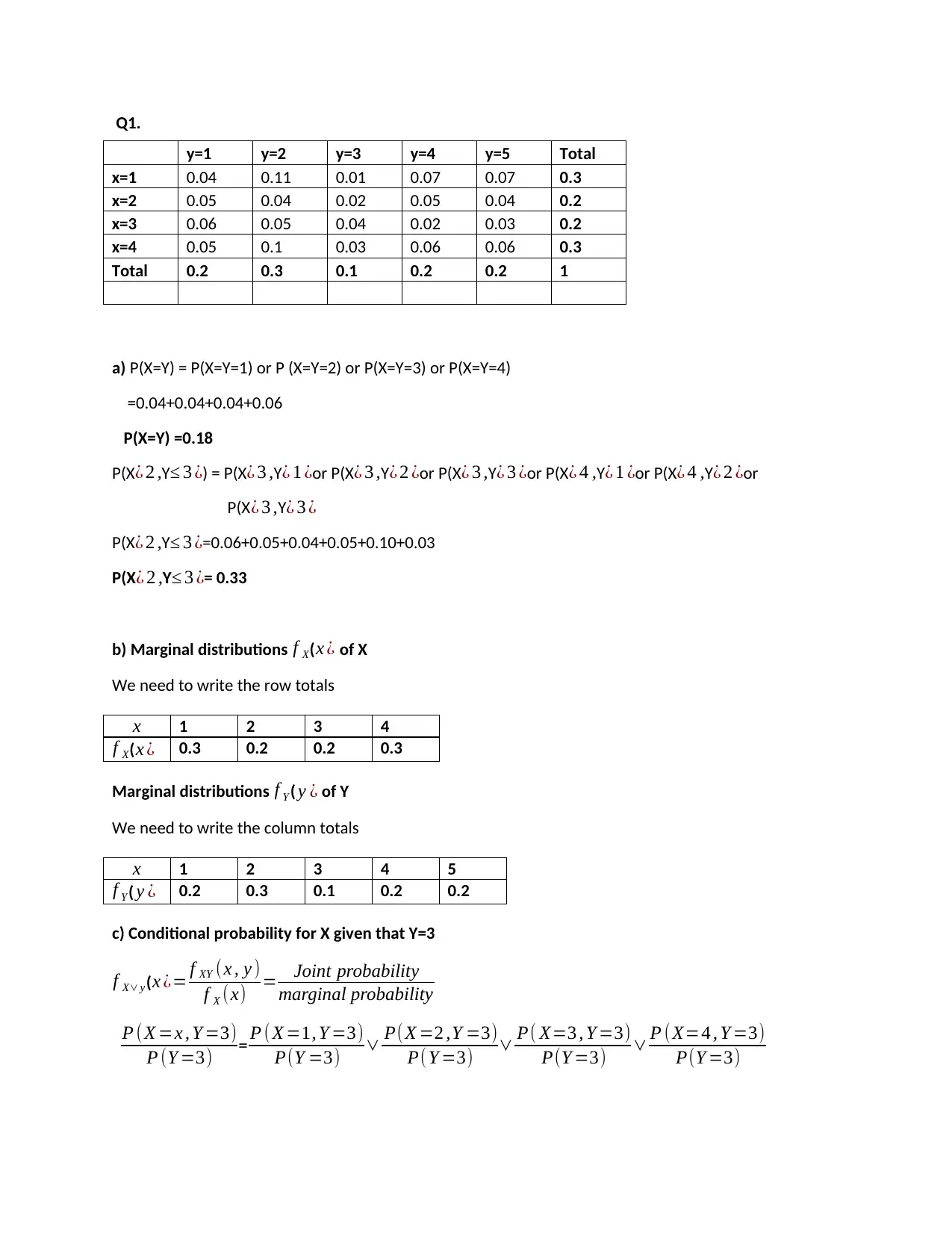
Q1.
a) P(X=Y) = P(X=Y=1) or P (X=Y=2) or P(X=Y=3) or P(X=Y=4)
=0.04+0.04+0.04+0.06
P(X=Y) =0.18
P(X¿ 2 ,Y≤ 3 ¿) = P(X¿ 3 ,Y¿ 1 ¿or P(X¿ 3 ,Y¿ 2 ¿or P(X¿ 3 ,Y¿ 3 ¿or P(X¿ 4 ,Y¿ 1 ¿or P(X¿ 4 ,Y¿ 2 ¿or
P(X¿ 3 ,Y¿ 3 ¿
P(X¿ 2 ,Y≤ 3 ¿=0.06+0.05+0.04+0.05+0.10+0.03
P(X¿ 2 ,Y≤ 3 ¿= 0.33
b) Marginal distributions f X(x ¿ of X
We need to write the row totals
Marginal distributions f Y ( y ¿ of Y
We need to write the column totals
c) Conditional probability for X given that Y=3
f X∨ y ( x ¿= f XY (x , y )
f X (x) = Joint probability
marginal probability
P (X =x , Y =3)
P (Y =3) = P ( X =1, Y =3)
P(Y =3) ∨ P(X =2 ,Y =3)
P(Y =3) ∨ P( X=3 , Y =3)
P(Y =3) ∨ P (X=4 , Y =3)
P(Y =3)
y=1 y=2 y=3 y=4 y=5 Total
x=1 0.04 0.11 0.01 0.07 0.07 0.3
x=2 0.05 0.04 0.02 0.05 0.04 0.2
x=3 0.06 0.05 0.04 0.02 0.03 0.2
x=4 0.05 0.1 0.03 0.06 0.06 0.3
Total 0.2 0.3 0.1 0.2 0.2 1
x 1 2 3 4
f X( x ¿ 0.3 0.2 0.2 0.3
x 1 2 3 4 5
f Y ( y ¿ 0.2 0.3 0.1 0.2 0.2

P (X =1, Y =3)
P(Y =3) = 0.01
0.1 =0.1
P ( X =2, Y =3)
P(Y =3)
0.02
0.1 =0.2
P (X =3 ,Y =3)
P(Y =3)
0.04
0.1 =0.4
P ( X =4 , Y =3)
P(Y =3)
0.03
0.1 =0.3
Conditional probability of X given that Y=3
d) Independence
For discrete variables, independence means that the probability in a cell must be the product of the
marginal probability of its rows and columns.
In row 1 and column 1, the probability is 0.04
However the product of marginal probability is 0.2×0.3=0.06
0.04≠ 0.06
X and Y are dependent (not independent) since 0.04 ≠ 0.06
Q2.)
Suppose X and Y are independent.
Let 0≤ k ≤ m+n
P(X+Y=k) =∑
i=0
k
P( X=i , Y =k −i)
∑
i=0
k
P ( X =i ) P(Y =k −i)
But P ( X=i ) =(m
i ) pi
(1− p)m −i and P(Y =k−i)=( n
k−i ) pk−i (1−p)n−k +i
∑
i=0
k
P ( X =i ) P(Y =k −i) becomes
=∑
i=0
K
(m
i ) pi (1−p)m−i(( n
k−i ) pk−i (1−p)n−k +i
x 1 2 3 4
f X∨ y=3(
x ¿
0.1 0.2 0.4 0.3

= pk (1−p)n +m−k
∑
i=0
k
(m
i )( n
k −i )
Taking (n+ m
k )=∑
i=0
k
(m
i )( n
k −i )
= pk (1−p)n +m−k
∑
i=0
k
(m
i )( n
k −i ) is reduced to
¿ (n+m
k ) pk (1−p)n +m−k
Thus we may conclude that X+Y have a binomial distribution with the parameters m+n and p.
Q3).
a)
We need to draw the region D which corresponds to 0 ≤ y ≤ 1. This is the region above y ≥0 and below
the line y=1.
The line y=1 intersects the line x=0 and x=2 at points (0,1) and (2,1).
Thus we have g1 ( x ) =1∧f 2 ( x ) =1
∫∫ f ( x , y ) dA=∫
0
2
∫
0
1
C x2 y3 dydx
¿ C∫
0
2
[∫
0
2
1
4 x2 y 4
]0
1
dx
¿ C∫
0
2
1
4 x
2
=1
y=1
y=0
x=2
x=0

¿ 8
12 C=1
C= 12
8 = 3
2
Hence
f ( x , y )= { 3
2 x2 y3
0 Otherwise
for 0 ≤ x ≤2
f ( x , y ) = { C x2 y3
0 Otherwise for 0 ≤ x ≤2 , 0 ≤ y ≤ 1
b)
P( X ≤ 1)
The intersection of D with the region X ≤ 1 is drawn
P ( X ≤1 ) =∫
0
1
∫
0
1
3
2 x2 y3 dydx
¿ 3
2 ∫
0
1
[ 3
8 x2 y4
]0
1
dx
¿
3
2∗3
8 ∫
0
1
x2 dx
¿ 9
16 [ 1
3 x3
]0
1
9
16 ∗1
3 = 3
16 =0.1875
c)
y=1
x-axis
2
1

c)
P(x+y>1)
We need draw the intersection of D with the region x+y>1
Y
1
1 2 x
Y=1-x
P(x+y>1) =∫
0
1
∫
0
1− x
( 3
2 x ¿¿ 2 y3 )dydx ¿ +∫
1
2
∫
0
1
( 3
2 x¿ ¿ 2 y3 )dydx ¿
¿ 3
8 ∫
0
1
¿ ¿ + 3
8 ∫
1
2
¿ ¿
¿ 3
8 ∫
0
2
¿ ¿ )dx
= 3
8 ∫
0
1
¿ ¿ )dx + 3
8 ∫
1
2
x2 dx
= 3
8 ¿
3
8 ¿) + 1
8 (8
3 −1
3 )
¿ 1
280 + 7
24 = 31
105

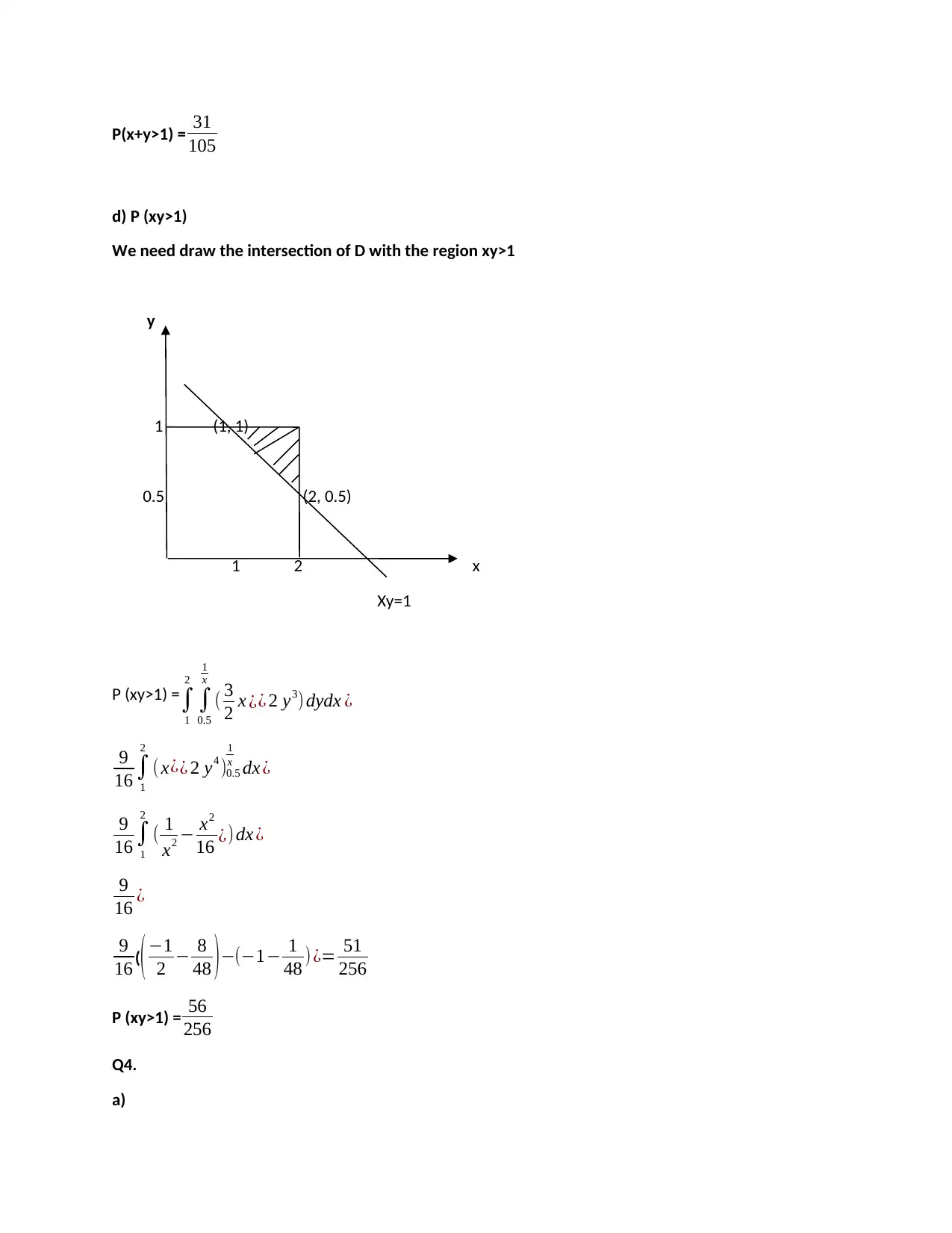
P(x+y>1) = 31
105
d) P (xy>1)
We need draw the intersection of D with the region xy>1
y
1 (1, 1)
0.5 (2, 0.5)
1 2 x
Xy=1
P (xy>1) =
∫
1
2
∫
0.5
1
x
( 3
2 x ¿¿ 2 y3) dydx ¿
9
16 ∫
1
2
( x¿¿ 2 y4 )0.5
1
x dx ¿
9
16 ∫
1
2
( 1
x2 − x2
16 ¿) dx ¿
9
16 ¿
9
16 (( −1
2 − 8
48 ) −(−1− 1
48 ) ¿= 51
256
P (xy>1) = 56
256
Q4.
a)

F ( x , y )=P ( { X ≤ x } ∩ { Y ≤ y } )
¿∫
0
x
∫
0
y
1
66 ( x3 +3 x y2 ) dtds
¿ 1
66 ∫
0
x
∫
0
y
( s3 +3 s t2 ) dtds
¿ 1
66 ∫
0
x
[ t s3 +s t2 ]t=0
t= y
ds
¿ 1
66 ∫
0
x
[ y s3 +s y3 ]t =0
t = y
ds
¿ 1
66 ( 1
4 y s4 + 1
2 s2 y3
)s=0
s= x
¿ 1
66 ( y x4 + 1
2 x2 y3
)
¿ 1
66 y x4 + 1
122 x2 y3
F(x, y) =0 for x<0 and y<0
F(x, y) =1 for x≥1 or y≥1
When x≥2 and 0<y<2 the cdf is F (2 , y )= 8
33 y
F(x, y) = { 1
66 ( x3 +3 x y2 )
0 ot h erwise
0<x<2, 0<y<3
Cdf is F (2, y) = 8
33 y + 1
33 y3
When y≥ 3∧¿0<x<2 the cdf is
Cdf is F(x, 2) = 1
33 x4 + 2
33 x2
Hence

F(x, y)=
{ 0 w h en x ≤ 0 , y ≤ 0
8
33 y + 1
33 y3 x ≥ 2, 0< y<3 ,
1
33 x 4+ 2
33 x2 y ≥ 3 , 0< x <2
1
66 x4 y+ 1
132 x2 y20 <x <2 ,0< y<3
1 x ≥ 2, y ≥3
b)
P [( 1
2<x<1) (1< y < 5
2 ) ¿ ¿ =
= F (1, 5
2 ¿−¿ F (1, 1 ¿−F ( 1
2 , 5
2 ) + F ( 1
2 ,1 )
= 5
32 − 1
44 − 127
4224 + 1
132 = 183
1408
=P [( 1
2<x<1) ∩ (1<y< 5
2)] = 183
1408
c)
Marginal pdf f X( x ¿ d
dx ¿( x ¿ ¿ where f X( x) equals to the limit of F(x, y) as y tends to infinity.
f X(x ¿=
{ 1
33 x4 + 2
33 x2 0< x <2
0 x ≤ 0
1 x ≥ 2
d
dx ¿(x ¿ ¿= 4
33 x3 + 4
33 x
Hence f X( x ¿=
{ 4
33 x3 + 4
33 x 0<x <2
¿ 0 otherwise

Marginal pdf f Y ( y ¿ of Y
Using the same argument as above
f Y ( y ¿=
{ 8
33 + 1
11 y2
0 otherwise
0<y<3
d)
For 0< x <2 , 0< y <3
Conditional pdf gX( x∨ y ¿
gX(x∨ y ¿= F (x , y )
f Y ( y ) = Joint probability
marginal probability
gX( x∨ y ¿= F (x , y )
f Y ( y ) =
1
66 ( x3 +3 x y2 )
8
33 + 1
11 y2
gX( x∨ y ¿= x3 +3 x y2
16+6 y2
gX( x∨ y ¿= x3+3 x y2
(16+6 y2)
gX(x| y )=
{ x3 +3 x y2
(16+6 y2 ) 0< x <2 , 0< y <3
0 otherwise
e)
When y= 3
2 we shall have

gX(x∨ y ¿=
x3 +3 x( 3
2 )
2
16+6 ¿ ¿
gX(x∨ y =3
2 ¿=
x3+ 27
4 x
29.5
Hence
gX( x| 3
2 )=
{ x3 + 27
4 x
29.5 0<x <2
0 otherwise
gX(x|3
2 )= { 2
59 (x3 + 27
4 x)0< x <2
0 otherwise
5.)
Suppose that X and Y are independent and we also have
F(x, y) = {96 x2 y2 for 0< x< 1
2 , 0< y<1
0 otherwise
We shall first obtain the marginal pdf of X and Y using the steps below.
FX ( x ¿=∫
0
1
96 x2 y2 dy
=¿
=24 x2 (1)3=24 x2
FX (x ¿=24 x2
FY ( y ¿=∫
0
0.5
96 x2 y2 dx
=¿
=32(0.5)3 y2=4 y2
FY ( y )=4 y2
FX ( x )FY ( y)=(24 x2 ¿ ( 4 y2 ) =96 x2 y2

Thus F(x, y) = FX (x ) FY ( y)=96 x2 y2
We therefore conclude that for two continuous random variables that are independent, the joint pdf
is equal to the product of marginal cdf of X and marginal cdf of Y.