University Maths Assignment: Matrices, Calculus and Equation Solving
VerifiedAdded on 2022/08/12
|8
|536
|41
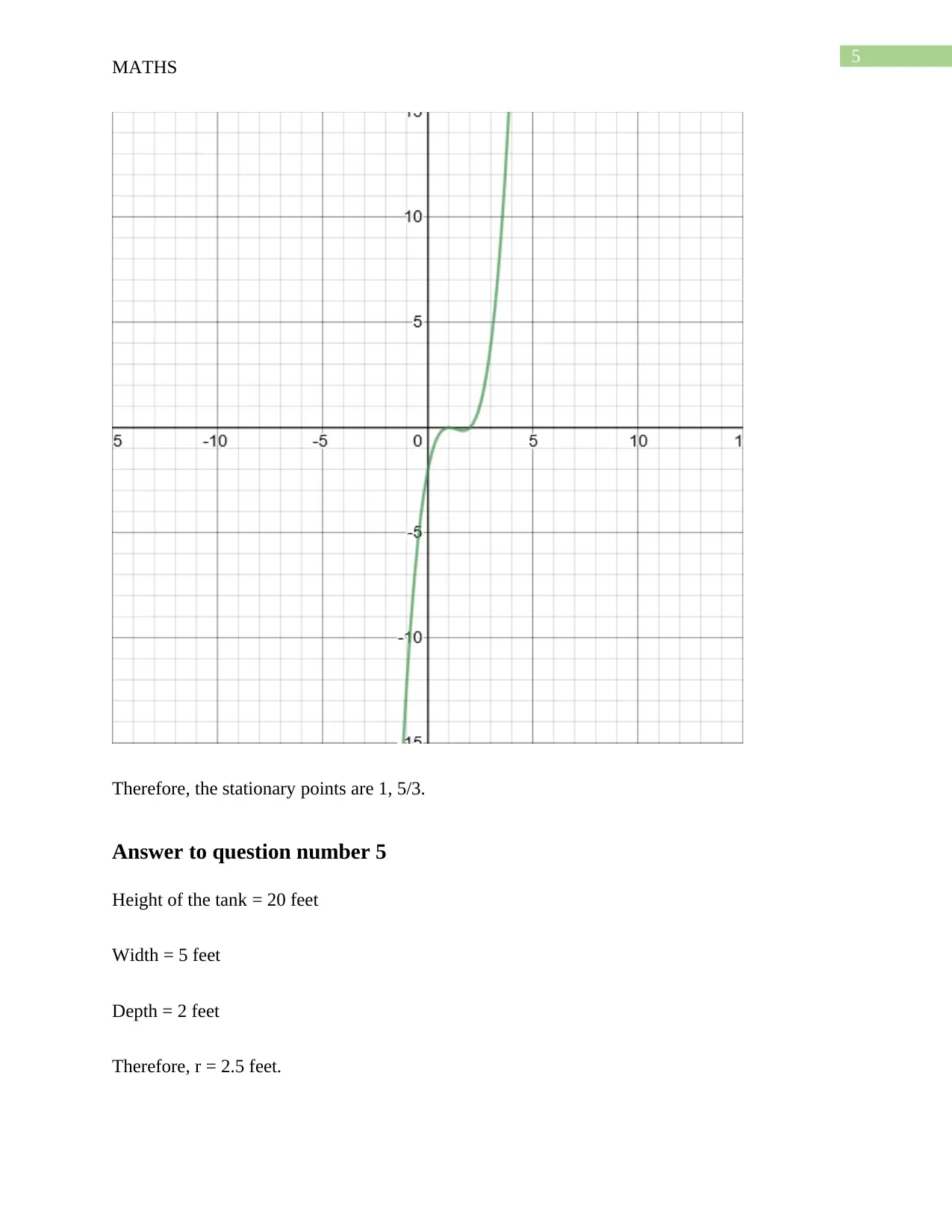
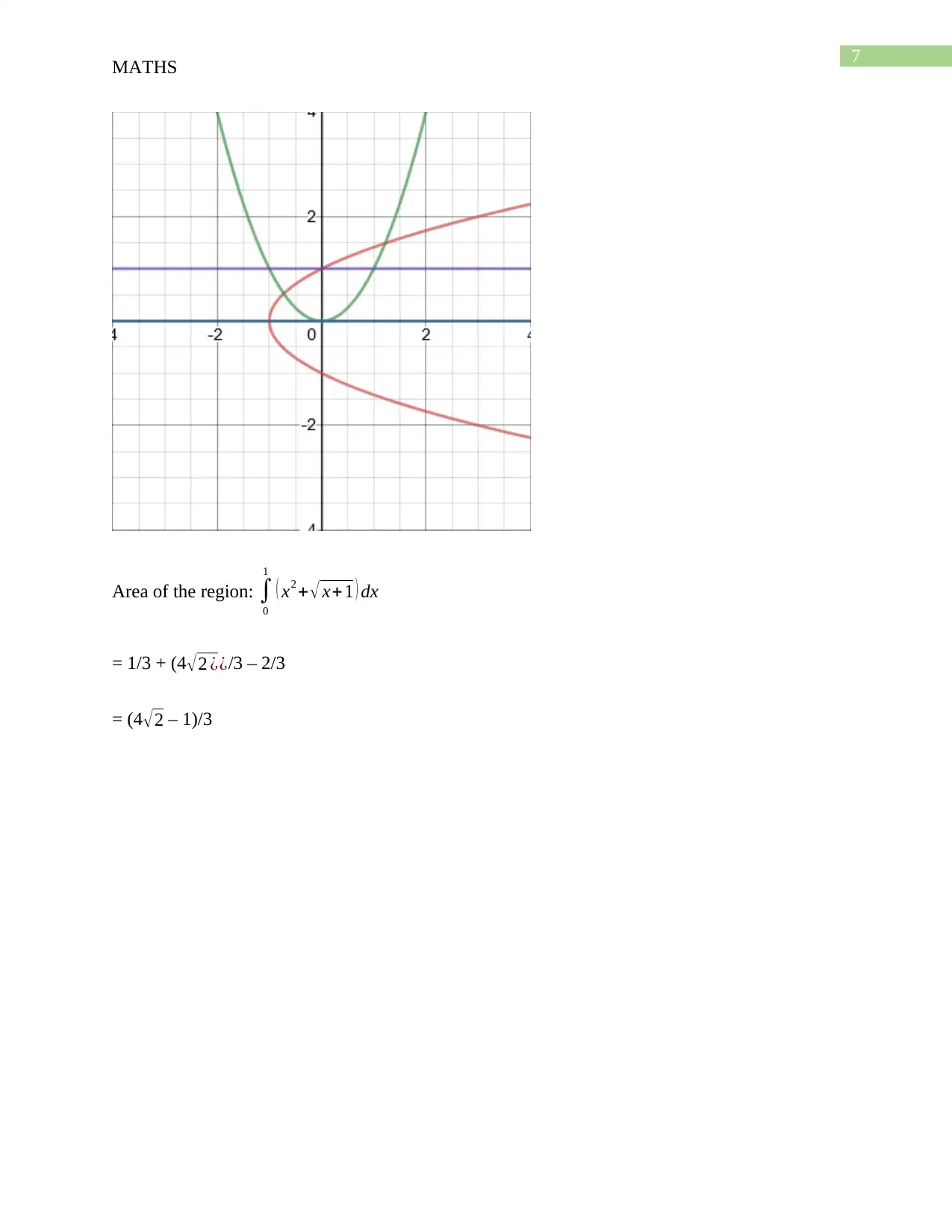
Homework Assignment
AI Summary
This document presents a complete solution to a Maths assignment covering a range of topics. The assignment begins with matrix operations, including finding a matrix C given a matrix equation, calculating the inverse of a matrix, and evaluating determinants. It then moves on to solving a system of linear equations using Gaussian elimination. The assignment also involves a practical problem involving trigonometry to calculate the height of two buildings using angles of elevation and depression. Furthermore, the solution includes finding stationary points of a function and solving a related calculus problem, including integration. Finally, it covers a volume calculation problem involving a tank and the time required to fill it. This comprehensive solution provides detailed steps and explanations for each problem, offering a valuable resource for students studying mathematics.
1 out of 8













![[object Object]](/_next/static/media/star-bottom.7253800d.svg)