Mathematics Assignment

This Mathematics assignment covers topics such as cosine functions, frequency, turning points, velocity, acceleration, and integration. It also includes solutions to problems on finding the maximum value of current, volume of a rectangle, RMS, and length of an arc.

Mathematics Assignment
Student Name
Institution
Date of submission

Part A
Question 1
a. Period T =0.4 , A=3.6 ,∧ phase angle=−π
12
The general format for a cosine function is given by f (t)= AcosB ( x +C ) + D
Filling the parameters
A is the amplitude which is given as 3.6
T = 2 π
B
this means B= 2 π
T = 2 π
0.4 =5 π
C is the phase angle at is given as −π
12
D is not indicated meaning it’s not there
Filling in the parameters in the equation we have
f (t)=3.6 cos 5 π (t− π
12 )
b. Frequency is given by
f = 1
T = 1
0.4 =5/2
c. f (t)=3.6 cos 5 π (t− π
12 )
2.16=3.6 cos 5 π (t− π
12 )
cos 5 π (t− π
12 )=0.6
This means that
cos−1 ( 0.6 )=5 π (t− π
12 )
53.1301=5 π (t− π
12 )
3.3824=(t− π
12 )

t=3.3824+ π
12 =3.6442
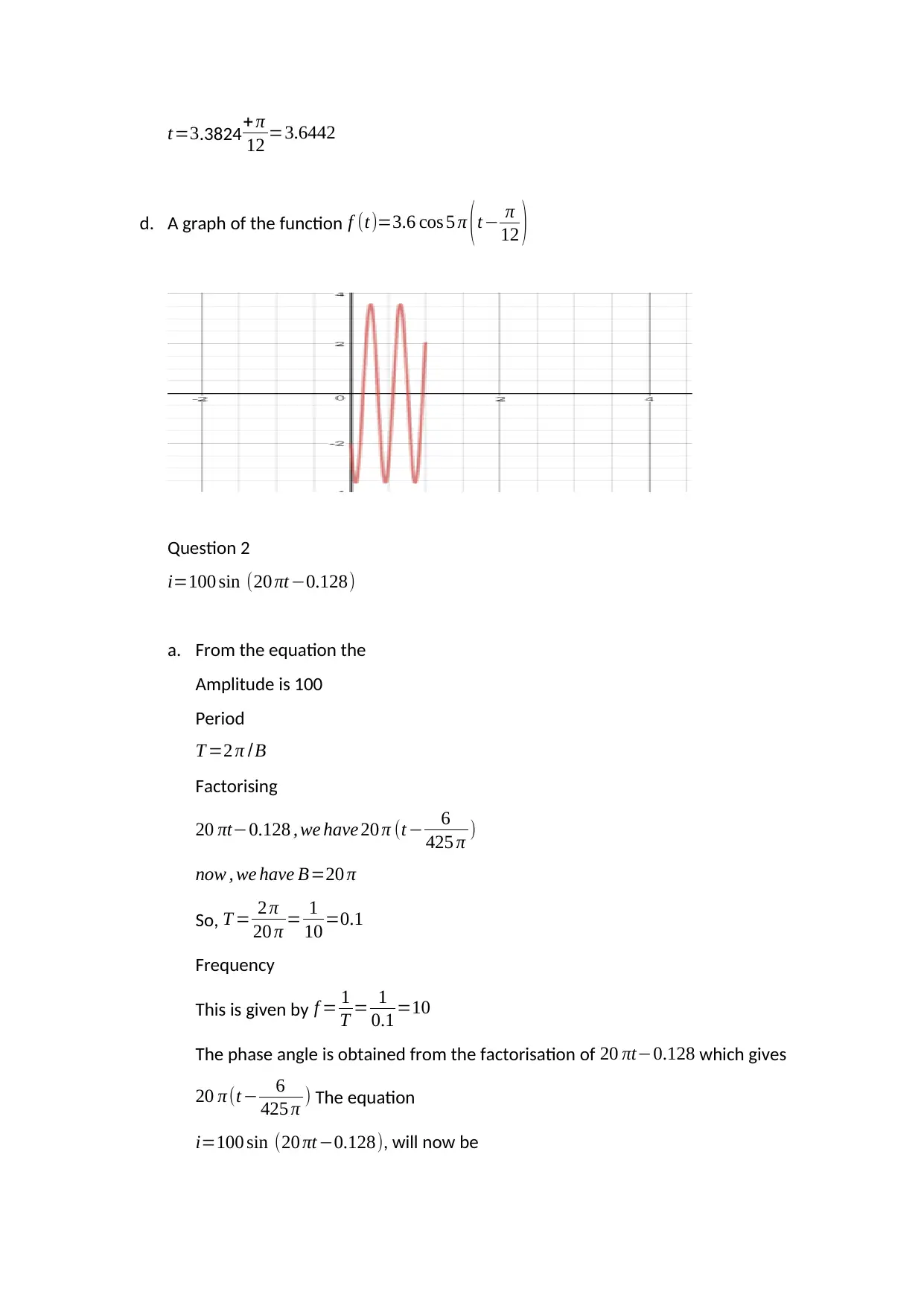
d. A graph of the function f (t)=3.6 cos 5 π (t− π
12 )
Question 2
i=100 sin (20 πt−0.128)
a. From the equation the
Amplitude is 100
Period
T =2 π /B
Factorising
20 πt−0.128 , we have 20 π (t − 6
425 π )
now , we have B=20 π
So, T = 2 π
20 π = 1
10 =0.1
Frequency
This is given by f = 1
T = 1
0.1 =10
The phase angle is obtained from the factorisation of 20 πt−0.128 which gives
20 π (t − 6
425 π ) The equation
i=100 sin (20 πt−0.128), will now be

i=100 sin 20 π (t− 6
425 π )
hence the phase angle=¿- 6
425 π ¿
b. When t=o ,i is?
i=100 sin (0−0.128),
This gives −0.2234 amperes
c. When t=0.02
i=100 sin (2
5 π −0.128),
¿ 1.9697 amperes
d. First reaches 50
50=100sin (20 πt−0.128), what is t
0.5=sin (20 πt−0.128)
30= (20 πt −0.128)
t=0.4795 seconds
e. Next reaches 50
This will be 0.4795+T =0.4795+0.1=0.5795 seconds
f. Fist reaches a maximum
From the equation the maximum is 100 amperes
Therefore 100=100sin (20 πt−0.128), now we find t
1=sin (20 πt−0.128)
90=20 πt−0.128¿
t=1.4344 seconds
Question 3
a. The turning points
dy
dx =12
x +2 x −10=0
To get the values of x we obtain the roots of the equation

2 x2 −10 x +12=0
Using the quadratic formula
x=−b ± √ b2−4 ac
2 a
we getthe values of x as 2 and 3
At these values of x, we use the relationship between y and x to get the values of y
as −7.68∧−7.82respectively .
This gives the coordinates of the turning points as
( 2 ,−7.68 )∧(3 ,−7.82)
Classification of the points
Using the sign rule
x 2.5 3 3.5
dy
dx
-0.5 0 1.5
This indicates that the point (3 ,−7.82) is a minimum point.
Now for point ( 2 ,−7.68 )
x 1.5 2 2.5
dy
dx
1.5 0 -0.5
This shows that this is a maximum point
b. Coordinates of the point of inflexion
The function has turning points at points x equal 2 and x equals 3, neither of these
points is appoint of inflexion. The point of inflexion is therefore not in the graph of
this function.
c. A sketch of the curve

Question 4
f ( t )= 2
5 e0.5 t +1
We need a point where the gradient of the tangent to the equation if 2.35.
The gradient is given by d
dt =0.2e0.5 t +1
Now equation 0.2 e0.5 t +1=2.35 , whats t ?
e0.5 t +1=11.75
Taking ln of both sides we have
0.5 t+ 1=ln 11.75
t= ln 11.75+1
0.5 =2.93
Now t equals 2.93, we can calculate the value of f(t)
f ( t )= 2
5 e0.5∗2.95+1=4.71
Hence the coordinates are obtained as (2.93 , 4.71).
Question 5
¿ the expressioni=35 sin (100 πt +0.26)

The maximum value of the current is given by the amplitude which in this case is
35amperes
The time when it first occurs
35=35 sin ( 100 πt+ 0.26 ) , what is t
1=sin (100 πt+0.26)
90=(100 πt+ 0.26)
89.74=100 πt
t= 89.74
100 π =0.286 seconds
Question 6
a. x=2 t3 + 9
2 t2−5 t +1
The velocity is equal to the derivative of the distance equation
Hence v= dx
dt =6 t2 +9 t−5
b. Velocity at start 6 t2+9 t−5 , wheret is 0. Here we find
−5
after 2 seconds , we have 6 t2+ 9 t−5 , wheret =2
37 seconds.
c. At rest the velocity is 0, t is therefore
The root of 6 t2+9 t−5=0 , t=0.431∨−1.931 since time cannot be negative
we take time as 0.431 seconds
d. Acceleration is the change in velocity
¿ dv
dt =12t +9
e. Acceleration after 2 seconds is given by 12 t+9, at t =2. This gives a=33
f. When 12 t+9=16 , what is t
12 t=16−9
t= 7
9 =0.7778 seconds
g. Average velocity is given by final plus initial divided by 2
Now initial is−5.
Final is given by 6 t2+ 9 t−5 , at t=4 , which is127.

Average will be 127−5
2 =61m/s
Question 7
Volume of a rectangle equals surface area * length
This gives
2
√4.5=1.65
Getting the area, we have 1.652=2.73
Question 8
h= √1502−1002=111.8033
r =100
2 =50
Question 9
v= π r2 h
3
v 2=¿ 1.08 π r2 h
3
%age change will be obtained by ( 1.08−1
1 )∗100=8 %
Question 10
y= kwl3
d4
After the changes
y 2= k∗0.8 w∗1.01l3
1.015 d4 = 0.808 kwl3
1.015 d 4
The % change in y is
¿ y 2− y
y ∗100 %
¿
0.808 kwl3
1.015 d4 − kwl3
d 4
kwl3
d4
∗100 %
Upon factorising we obtain
−207
1015 ∗100 %=−20.39 %

Question 11
∫ 4 x2−9 x−19
2 x2 −7 x−4
From this we observe that the degree of the numerator is not less than the
degree of the denominator, to correct that we carry out a long division. This
break the polynomials to.
∫2+∫ 5 x−11
2 x2−7 x −4
∫2 dx=2 x
Now we integrate the remaining parts
∫ 5 x−11
2 x2−7 x −4 , here we use partial fractions
Factorising 2 x2 −7 x−4 , gives(x−4)(2 x+1)
Now
∫ 5 x−11
2 x2−7 x −4 =∫ 5 x−11
( x−4 )(2 x +1)
5 x−11
2 x2−7 x−4 = A
x−4 + B
2 x+ 1
Multiplying both sides by (x−4)(2 x+1) we have
5 x−11=2 Ax+ A+ Bx−4 B
This gives the following two equations
5 x=2 Ax +Bx
−11= A−4 B
now , A=4 B−¿11
5 x=8 Bx−22 x +Bx
27 x=9 Bx , B=3
A=1
Hence
∫ 1
x−4 + ¿∫ 3
2 x+ 1 ¿
∫ 1
x−4 =ln ( x−4 )

∫ 3
2 x+1 = 3
2 ln (2 x+1)
adding the parts we have ;
2 x+ ln ( x −4 )+ 3
2 ln ( 2 x +1 ) +c
Question 12
The by parts formula is given as
∫udv=uv−¿∫ vdu ¿
Now ∫2 xsin ( 4 x ) dx
u=2 x
dv =sin ( 4 x ) dx
du
dx =2
du=2 dx
v=∫ dv=∫sin ( 4 x ) dx
v=−1
4 cos (4 x )
Now putting thisinformation in the by parts formula we have,
¿ 2 x∗−1
4 cos ( 4 x )−∫ −1
4 cos ( 4 x )∗2 dx
¿−1
2 xcos ( 4 x ) −∫ −1
2 cos (4 x )dx
This gives the solution as
−1
2 xcos ( 4 x ) + 1
8 sin ( 4 x)
Question 13
The formula for calculating the mean value of a function is
¿ 1
b−a ∫
a
b
f ( x ) dx
¿ 1
0.8−0.5 ∫
0.5
0.8
5 e2 t−1 dt
10
3 ∗5∫
0.5
0.8
e2 t−1 dt=50
3 ∗ [ e2 t −1 ] , insertingthe boundaries we have

25
3 ∗( 1.8221−1 )=6.8508
Question 14
The RMS¿ √ 1
b−a ∫
a
b
y2 dx
¿ √ 1
4−1 ∫
1
4
(2 x3 +3 x )2 dx
calculating 1
4−1 ∫
1
4
(2 x3 +3 x)2 dx
Expanding (2 x3 +3 x )2 gives 4 x6 +12 x4 +9 x2
Integrating with respect to x we have
¿ 1
3∗
[ 4
7 x7+ 12
5 x5 + 9
3 x3
] , when the boundaries are incorporated we have
1
3 ( 12011.89−5.97 )= √4001.9733=63.26
Question 15
The formula for length of an arc is given by
L=∫
a
b
√ 1+(f ¿¿ 1( x ))2 dx ¿
We y2= 25
16 x3, this gives y= 5
4 x3 /4
f 1 ( x )= 15
8 x1/ 2
(f ¿¿ 1 ( x ) )2=225/ 8 x ¿
Replacing thevalues in the formula gives
L= ∫
1.25
2.75
√1+ 225
8 x dx
Using substitution method
u=1+ 225
8 x
du
dx = 225
8
dx= 8
225 du

∫ u1 /2∗8
225 du=
8
225∗u3/ 2
3/2
¿ 691
450 u3/ 2 replacing the value of u gives us 691
450 (1+ 225
8 x)
3 /2
Inserting the boundaries
691
450 ( 693.4362−217.4078 )=730.9681
Question 16
Volume about the y-axis is given by
¿ 2 π ∫
a
b
xydx`
The rotation through 180 degrees changes the sign of the boundaries to
t=−3 andt =−5
Now, calculating xy=ty= ( 4 t2+3t−2 ) t=4 t3+3 t2−2 t
Replacing the values in the formula we obtain 2 π ∫
−3
−5
4 t3 +3 t2−2 tdt
2 π [ t4 +t3−t2 ] ,
the boundaries
¿ 2 π ( 475−45 )=860 π
Question 17
a.

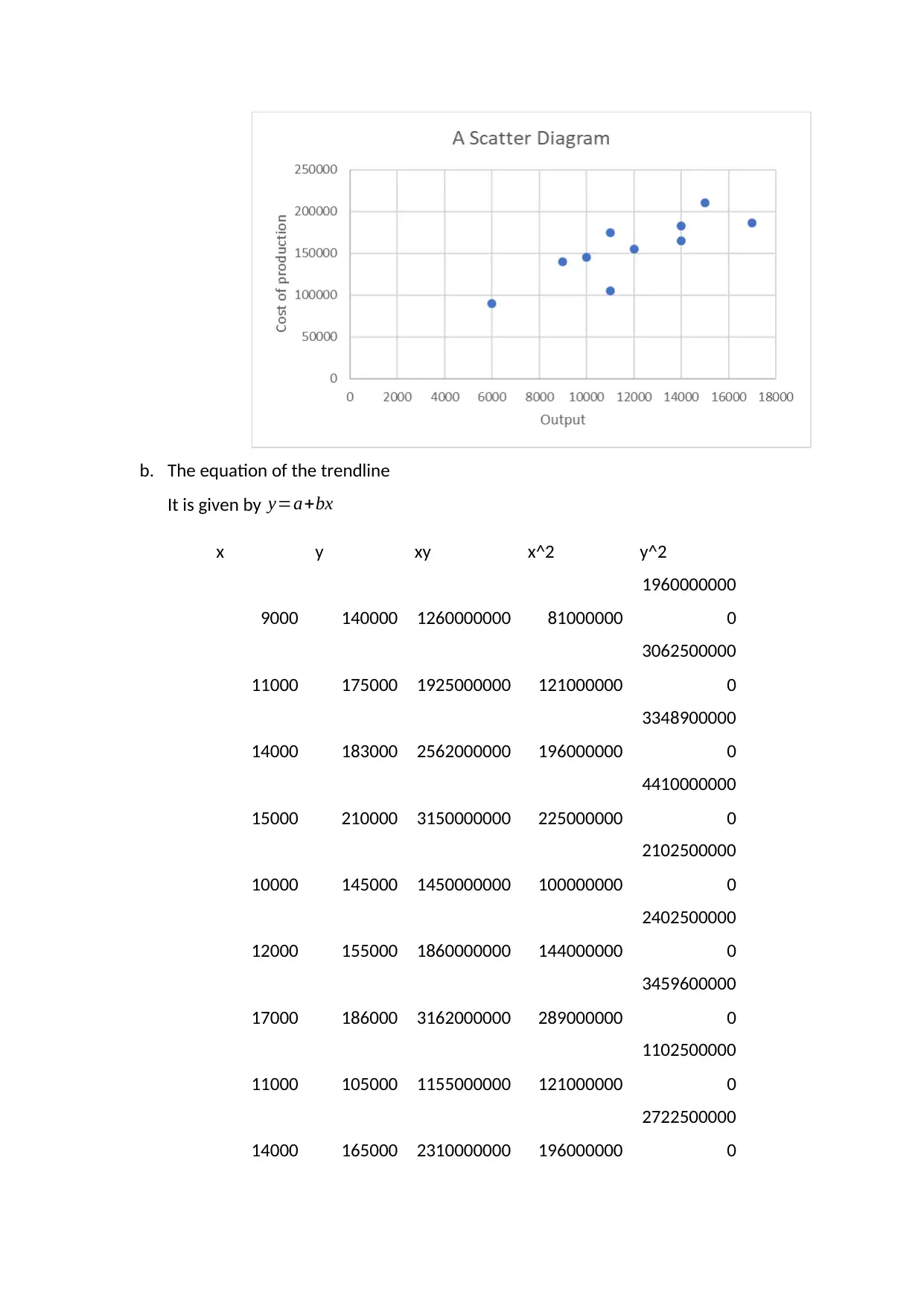
b. The equation of the trendline
It is given by y=a+bx
x y xy x^2 y^2
9000 140000 1260000000 81000000
1960000000
0
11000 175000 1925000000 121000000
3062500000
0
14000 183000 2562000000 196000000
3348900000
0
15000 210000 3150000000 225000000
4410000000
0
10000 145000 1450000000 100000000
2102500000
0
12000 155000 1860000000 144000000
2402500000
0
17000 186000 3162000000 289000000
3459600000
0
11000 105000 1155000000 121000000
1102500000
0
14000 165000 2310000000 196000000
2722500000
0

6000 90000 540000000 36000000 8100000000
Total 119000 1554000
1937400000
0 1509000000 2.5381E+11
mean 11900 155400
Square
mean
14161000
0
2.4149E+1
0
b=∑ xy−n μx μy
∑ x2−n μx
2 = 19374000000−( 10∗11900∗155400)
1509000000−(10∗141610000) =9.4876
a=μy−b μx=155400− ( 9.4876∗11900 ) =42497.56
The equation is thus given by y=42497.56+9.4876 x
This is also proven from the equation of the line of nest fit indicated in the graph
below
Is given by y=42497+9.4876 x
c. The Pearson’s correlation coefficient is obtained from the graph as r =0.8240 ,
By calculation we have
r = ∑ xy−n μx μy
√(∑ x2 −n μx
2)(∑ y2−n μy
2)
This is 19374000000−( 10∗119000∗155400)
√¿ ¿ ¿

this value indicates that the cost of production is strongly correlated to the output
during the 10 months period. The volume of output is therefore shown to be
responsible for at least 67.89% of the cost of production.
d. Using the equation y=9.4876 x + 42497 , when x is 19000, then y will be €
222761.40.
Part B
Question 1
Complex solution of the equation
4 x+ 8
x =3
Expressing the equation in a quadratic form we have
4 x2 −3 x +8=0
Applying the quadratic formula
We have
x=−b ± √ b2−4 ac
2 a
This gives
¿ 3± √(−3)2−(4∗4∗8)
2∗4
3± √ −119
8
√−119= √−1∗√119=10.9087 i
From this the complex solutions are
3± 10.9087 i
8
Question 2

a. z2
1∗z2
¿ ¿
¿
¿ 4−16 j+ 16 j2
¿(4−16 j+16 j2 ¿∗( 5+5 j )=112 j3−32 j2−52 j+20
b. z1∗z2
2 z3
(−2+ 4 j)∗(5+7 j )
2(−1−2 j)
¿ 28 j2+6 j−10
−(4 j +2)
Question 3
z1=8+i
z2=4−i
z3=−8−i
z4 =2−i
Question 4
a. 3 ¿
3 ¿
b. 3 ¿ ¿
c. ¿
d. 3 √ 6 cos ( 102 ) + jsin ( 102 )
Question 5
a. In exponential form
z=−3.62−4.78 j
−3.62 e−4.78 j

b . Will have 4 + 6−πj
7
Question 6
a. The locus is a circle with a radius 5 π
b. x2+ y2+2 gx+ 2 fy+c =0
z=x + jy will be a ˚withradius z+5
Question 7
a. 6.3 sin ( ωt ) −8.2 cos ( ωt ) =−1.9 sin ( ωt+5)
b. The solution will give
10 sin (ωt−34)
Question 8
a. 100+4.6=104.6
b. Total current is 250 amperes
c. 250
100 =2.5 volts
d. 250
4.6 =54.34 volts
e. 100
4.6 =21.73 volts
Question 9
a. Throwing a dice twice
Outcome
2nd throw
1st throw 1 2 3 4 5 6
1 1 2 3 4 5 6
2 2 4 6 8 10 12
3 3 6 9 12 15 16
4 4 8 12 16 20 24
5 5 10 15 20 25 30

6 6 12 18 24 30 36
Total outcome 36
Less than 15; 23
p ¿
b. We need the probability that the value of the selected card is either 5,6,7,8,9. The
total number of cards in a Dec with these values are
4∗5=20 , hence the probability will be 20
52 =5/13
Question 10
a. Different ways of choosing 5 cards
52∗51∗50∗49∗48=311875200ways
b. Ways of selecting two Aces
This
4∗3∗48∗47∗46=1245312
Now the probability of selecting two aces in the poker hand ¿ 1245312
311875200 =0.003993
c. Chances of selecting all cards from a single unit
52∗3∗2∗1∗0=0
The probability will be 0
A suit has only 4 cards, it is therefore impossible to select 5 cards which are of a
similar suit.
Question 11
P ( penalty is scored )= ( A∗S ) + ( B∗S )= ( 0.44∗0.7 )+ ( 0.56∗0.55 )=0.616
Where S is the probability of score and A/B is the probability of player A/B taking the
penalty.
Question 12
We need to select 7 questions from the available 10
Question 1 is selected in 1 way
Question two in 9 ways

question 3 in 8 ways…
Now the 7 questions will be selected in 1∗9∗8∗7∗6∗5∗4=60480 ways
Question 13
Ways of making the 4 dials 6∗6∗6∗6=1296 ways
Time taken to try all
1296∗5= 6480
60 = 108 minutes
24 =4 days 12 hours
Question 14
a. Angle between vector p and q
cos ( θ )= p . q
∥ p ∥∗∥q ∥
∥ p ∥= √ p 12+ p 22 + p 32= √32 +72 + (−2 )2= √62
∥q ∥= √ qi2+ q 22 +q 32= √ 42 +(−1)2 +12=3 √ 2
Now p . q= p 1q 1+ p 2 q 2+ p 3 q 3= ( 3∗4 ) + ( 7∗−1 ) + (−2∗1 )=3
cos ( θ )= 3
√62∗3 √ 2= √31
62
This gives θ=84.85 °
b. p∗q
p=3 i +7 j−2 k
q=4 i− j+ k
First, we form the matrix
[
i j k
3 7 −2
4 −1 1
]
Finding the determinant of the 3*3 matrix
¿ i [ 7 −2
−1 1 ]− j [ 3 −2
4 1 ]+k [3 7
4 −1]
¿ 5 i−11 j−31 k , this is the cross product of vector p and q
c. The area is given by

A=∥ p∗q ∥= √ ( p∗q ) 12+ ( p∗q ) 22 + ( p∗q ) 32= √ 52 + ( −11 ) 2 + ( −31 ) 2
¿ √ 1134=9 √14
d. Volume of tetrahedron
V =∥ p .( q∗r) ∥
( q∗r )=isthecross product of q and r
formingthe ¿
i j k
4 −1 1
5 −2 6
¿
getting the determinant of the matrix
i [ −1 1
−2 6 ]− j [ 4 1
5 6 ] + k [ 4 −1
5 −2 ] =−4 i−19 j−3 k
Now, we get the dot product
p=3 i +7 j−2 k
( q∗r )=¿-4 i−19 j−3 k
¿ ( 3∗−4 ) + ( −19∗7 ) + ( −2∗−3 ) =−139
the magnitude is 139 which givesus the volume
Question 15
We use the formula
a ( x−x0 ) +b ( y− y0 ) +c ( z−z0 ) =0
finging thea, b and c
We get a vector perpendicular to the plane
This is obtained by getting a cross product of number of vectors. Now computing
the vectors, we have
Points p=(5 ,−7,0)
q= ( −9 ,−18,22 )
r =(0,0,0)
Vector pq= ( −14 ,−11,22 ) ∧vector qr =(−5,7,0)
taking the crossproduct of the vectors we have
¿

[
i j k
−14 −11 22
−5 7 0
]
Getting its determinant
i [−11 22
7 0 ]− j [−14 22
−5 0 ]+k [−14 −11
−5 7 ]=−154 i−100 j−153 k
These values give us ( a , b , c )=(−154 ,−100 ,−153)
Taking point p and filling the values in the original formula we find the equation
of the line as
−154 ( x−5 ) −100 ( y+ 7 ) −153 z=0
Question 16
Points
A=(12 ,−4,2)
B=(−6,3 ,−3)
C=(10,15,9)
the general formulais givenby=a ( x−x0 ) +b ( y− y 0 )+ c ( z −z0 )=0 to get
(a , b , c ) we find a perpendicular vector to the plane
Computing vectors
AB=(−7,7 ,−5)
BC=(16,12,12)
getting the ˙¿product of the vectors
Matrix
[
i j k
−7 7 −5
16 12 12
]
Determinant
=i [ 7 −5
12 12 ]− j [−7 −5
16 12 ]+ k [−7 7
16 12 ]=144 i+4 j−196 k
This gives the value of ( a , b , c ) = ( 144,4 ,−196 )
Taking point A=(12 ,−4,2)
We can fill in the values in the equation to obtain the equation of the plane as
144 ( x−12 ) + 4 ( y +4 )−196 ( z−2 )=0

Question 17
x +6 y−5 z=20
7 x− y−11 z=14
x=20−6 y +5 z
x=2+ 1
7 y + 11
7 z
Equating the two
20−6 y+ 5 z =2+ 1
7 y +11
7 z
z=−21
4 + 43
24 y
Writing x in terms of y
x=−25
4 + 71
24 y
Now suppose y=t , then x=−25
4 + 71
24 t ,∧z=−21
4 + 43
24 t
Th above forms asset of parametric equations that gives us the line of
intersection of the two planes.
Question 18
The planes are
x−2 y + z=7∧¿
−2 x+ 4 y−2 z=−14
Question 19
d
dt =−7+1.2 e0.2t =0
−7
1.2 =e0.2t
ln (−7
1.2 )=0.2t ,t=0
Question 20
a. A plot of the graph

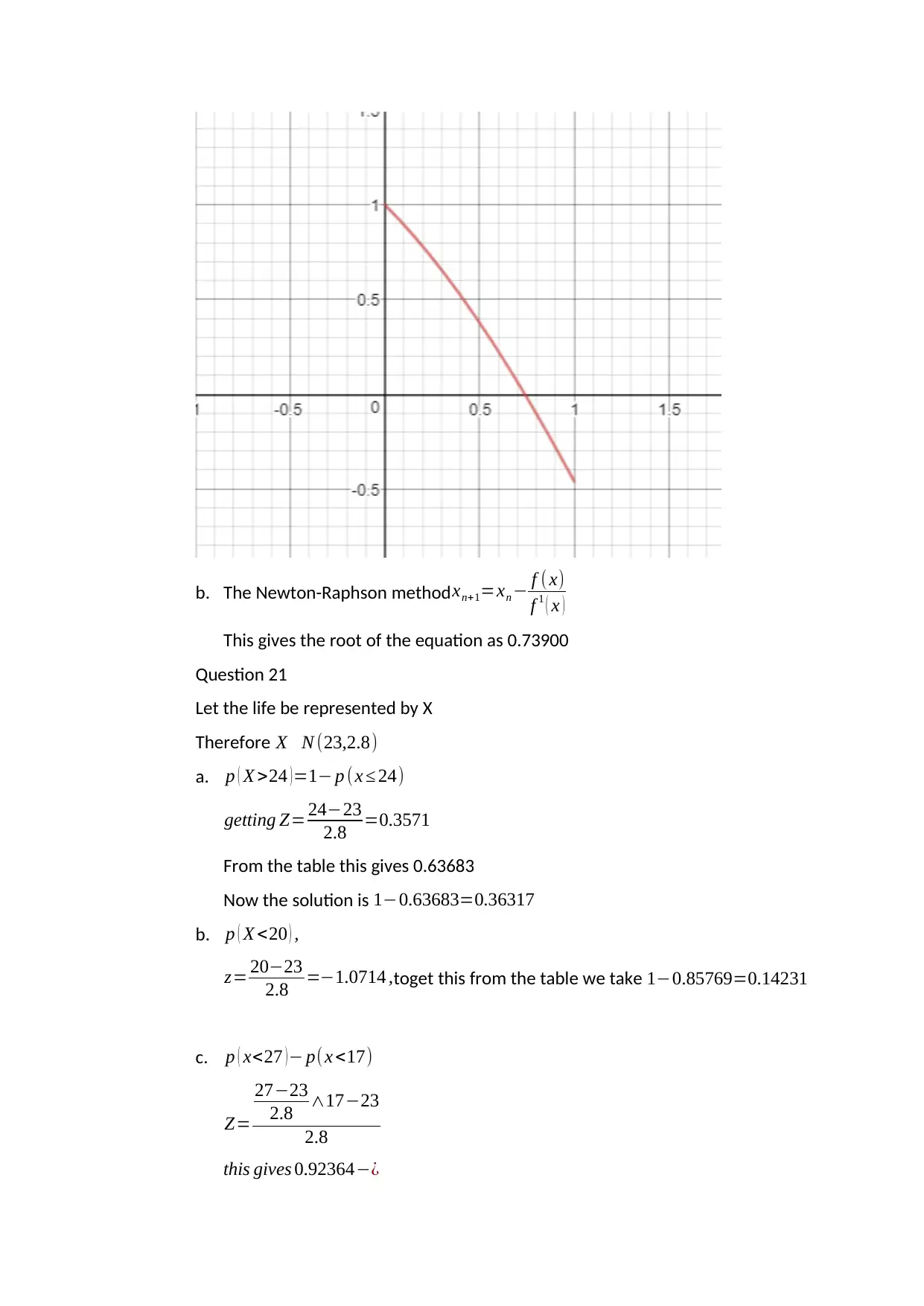
b. The Newton-Raphson method xn+1=xn − f ( x)
f 1 ( x )
This gives the root of the equation as 0.73900
Question 21
Let the life be represented by X
Therefore X N (23,2.8)
a. p ( X >24 ) =1− p (x ≤ 24)
getting Z= 24−23
2.8 =0.3571
From the table this gives 0.63683
Now the solution is 1−0.63683=0.36317
b. p ( X <20 ) ,
z= 20−23
2.8 =−1.0714 ,toget this from the table we take 1−0.85769=0.14231
c. p ( x<27 )− p( x <17)
Z=
27−23
2.8 ∧17−23
2.8
this gives 0.92364−¿

Question 22
a. Probability of defective is 0.15, taking binomial distribution
5 ∁ 0∗0.150∗ (1−0.15 )5=0.4437
b. At most 2 means 0,1 and 2
5 ∁ 0∗0.150∗ (1−0.15 )5 +5 ∁ 1∗0.151∗( 1−0.15 ) 4 +5 ∁ 2∗0.152∗( 1−0.15 )3 =0.9734
c. This is obtained by 1- less than three bolts will be defective
That is 1−0.9734=0.02661

References
Benesova, B. a. K. M., 2017. Weak Lower Semicontinuity of Integral Functionals and
Applications.. SIAM Review, 59(4), p. 703–766.
Cassel, K. W., 2013. Variational Methods with Applications in Science and Engineering, s.l.:
Cambridge University Press.
Stolz, M., 2002. The History Of Applied Mathematics And The History Of Society. Synthese,
133 (1), p. 43–57.
University of Strathclyde, 2008. Industrial Mathematics, s.l.: University of Strathclyde.