Thomas Edison State University - MAT-121: College Algebra Assignment 6

This document presents solutions to a college algebra assignment, focusing on various methods for solving systems of equations and their real-world applications. The assignment covers determining solutions to systems of equations, solving systems using substitution and addition, and solving graphically. Real-world problems include break-even analysis for a band's performance, calculating the number of floral arrangements needed to break even, and solving mixture problems. Additionally, the assignment addresses solving systems of three equations with three variables, solving non-linear systems of equations, and solving systems of inequalities graphically. The solutions provide detailed steps and explanations for each problem.

Section:7.1
Solution.1:
Given:
y+ 3x = 5……………..(1)
2x + y = 10…………..(2)
Ordered pair = (1,8)
So, x = 1, y =8;
By putting the value of x and y in equation 1;
8 + 3(1) = 5
11 = 5
L.H.S is not equal to R.HS.
Hence the ordered pair is not the solution of equation (1)
Now, By putting the value of x and y in equation 2;
2(1) + 8 = 10
10 = 10
L.H.S is equal to R.HS.
Hence the ordered pair is the solution of equation (2)
Solution.2:
Given:
3x- y =4………..(1)
2x + 2y = 12……(2)
From equation (2);
2x = 12 - 2y
x = 6 – y……..(3)
By substituting the value of x in equation (1);
3(6 – y) - y =4

18 – 3y – y = 4
-4y = 4-18
y = 14/4
By substituting the value of y in equation (3);
x = 6 – 14/4
x = (24-14)/4
x= 10/4.
Solution.3:
Given:
7x + y = 15………….(1)
-2x + 3y = -1…………(2)
Multiplying equation (1) with 3;
21x +3y = 15…………..(3)
-2x +3y = -1
+ - +
---------------------
19x = 16
x = 16/19
Substituting the value of x in equation (1);
7 × 16
19 + y = 15
y = 173 /19
Solution.4:
Given:
x + 2y = -4………….(1)

-2x + 3y = -13…………(2)
Multiplying equation (1) with 2;
2x +4y = -8…………..(3)
-2x +3y = -13
+ - +
---------------------
y = 5
Substituting the value of y in equation (1);
x + 2(5) = -4
x = -14
Graphical:
Solution.5:
Given:
5x +3y = 12…………..(1)
-10x – 6y = 8…………(2)
In equation(1)
If, x =0;
Then y = 12/3 = 4; (0,4)
If, y =0;
Then x = 12/5 = 2.4; (2.4,0)
In equation(2)
If, x =0;
Then y = -8/6 = 1.33; (0,1.33)
If, y =0;
Then x = -8/10 = 0.8; (0.8,0)

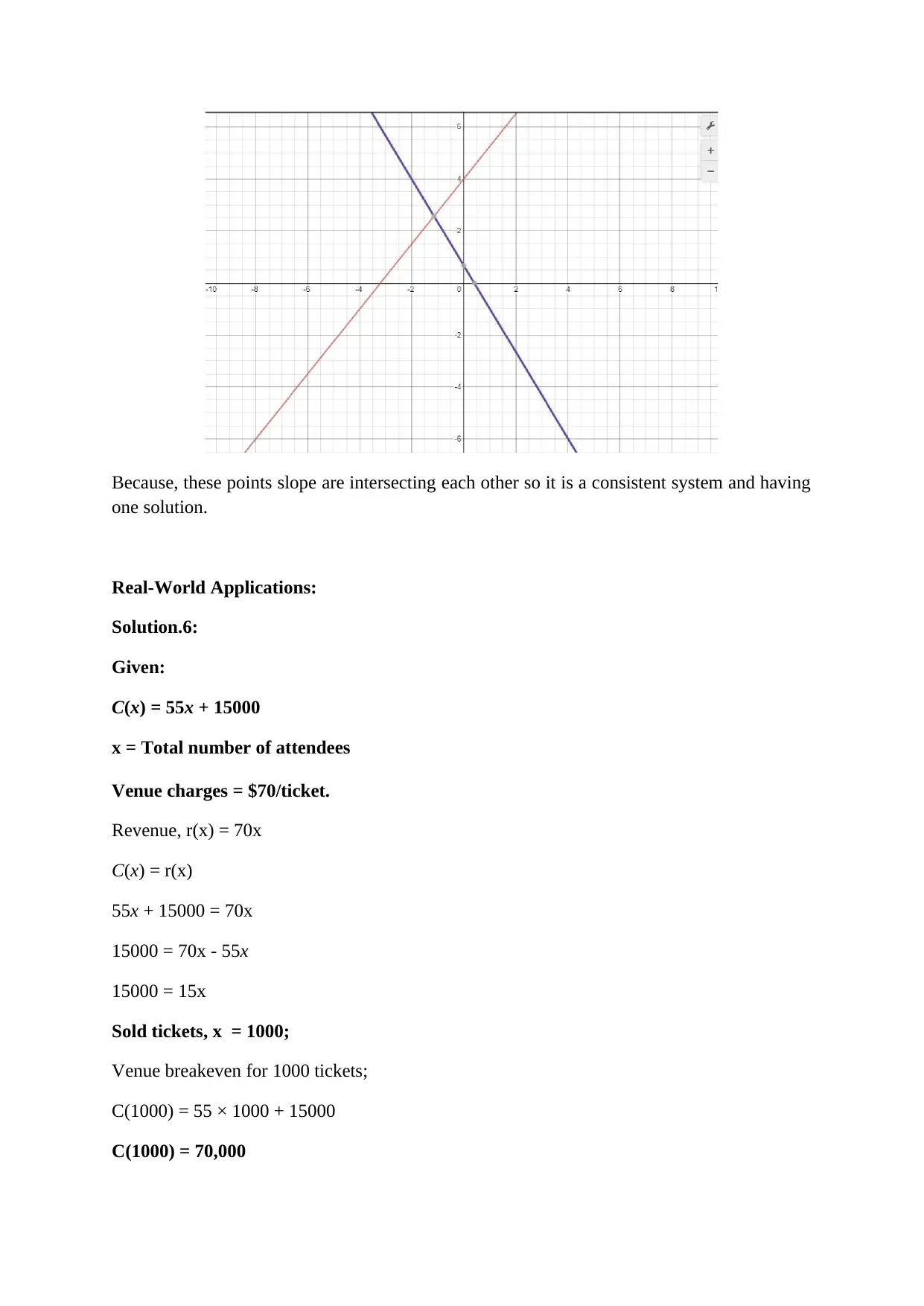
Because, these points slope are intersecting each other so it is a consistent system and having
one solution.
Real-World Applications:
Solution.6:
Given:
C(x) = 55x + 15000
x = Total number of attendees
Venue charges = $70/ticket.
Revenue, r(x) = 70x
C(x) = r(x)
55x + 15000 = 70x
15000 = 70x - 55x
15000 = 15x
Sold tickets, x = 1000;
Venue breakeven for 1000 tickets;
C(1000) = 55 × 1000 + 15000
C(1000) = 70,000

Solution.7:
Given:
cost = 15,000
each floral arrangement costs = 17$
each arrangement sold costs = 25$
Profit from each arrangement = 25 - 17 = 8$
Number of Arrangements for Break-Even = 15,000/8 = 1875$
Solution.8:
Parameters Total amount of
solution
Percentage Saline Total amount of
Saline
Starting solution 20 35% 7
Solution Added x 15% 0.15x
Resulting Solution 20+x 48% 0.48(20+x) = 0.15x
+7
0.48(20+x) = 0.15x +7
9.6 + 0.48x = 0.15x +7
x = -7.87
15% of solution mixture = -7.87 × 0.15 = -1.181Gallons
For 48% of solution mixture:
20 + (-0.787) = 12.13
12.13 × 0.48 = 5.8244 Gallons
Solution.9:
Suppose,
Price of children admission = x
Price of Adults admission = y
So,
4x + 2y = 133.50 $ ....................(1)

6x +4y = 235.50$ .....................(2)
Multiplying with 2 in equation (1);
8x + 4y = 267.00$ …………….(3)
6x +4y = 235.50$ .....................(2)
- - -
-----------------------------------------------
2x = 31.50
x = 15.75 $
Substituting the value of x in equation (1);
4 × 15.75 +2y = 133.50
63 +2y =133.50
2y = 70.5
y = 35.25$

Section: 7.2
Solution.10:
Given:
2x − 3y + 4z = 3……………..(1)
− x + 5y + 2z = 10…………..(2)
3x − 4y − z =− 9……………..(3)
Ordered triple :(-1, 1, 2)
For equation (1),
2x − 3y + 4z = 3………………(1)
2(-1) – 3(1) + 4(2) = 3
-2 -3 +8 = 3
3 = 3
For equation (2),
− x + 5y + 2z = 10…………..(2)
− (-1) + 5(1) + 2(2) = 10
1 +5 +4 = 10
10 =10
For equation (3),
3x − 4y − z =− 9……………..(3)
3(-1) – 4(1) – (2)=− 9
-3 -4 -2 = -9
-9 = -9
Solution.11:
Given:
x − 3y + 5z = 29 …………(1)

3x + y − 4z =− 9 …………(2)
4x − 3y + 7z = 46 …………(3)
From equation (2),
y = -9 + 4z + 3x
Substituting the value of y in equation 1;
x – 3 (-9 + 4z + 3x) + 5z = 29
x + 27 – 12z -9x +5z = 29
8x + 7z = 2…………………….(4)
Substituting the value of y in equation 3;
4x – 3 (-9 + 4z + 3x) +7z = 46
4x +27 -12 – 9x +7z = 46
5x +5z = -19…………………..(5)
Multiplying equation(4) with 5 and equation(5) with 7; we get;
40x +35z = 10
35x +35z = -133
- - +
---------------------------
5x = 143
x= 2.86
Substituting the value of x in equation 4;
8(2.86) + 7z = 2
z = -2.98
2.86 − 3y + 5(-2.98) = 29
2.86 − 3y – 14.9 = 29
-3y = 29 +12.9
y = 13.96

Solution.12:
Given:
x + y + z = 6, …………………(1)
3x − 2y + 4z = 37 …………….(2)
− 4x + 3y − 6z =− 53 …………(3)
Multiplying equation (1) with 4;
4x + 4y +4z = 24
3x − 2y + 4z = 37
- + - -
----------------------------
x + 6y = -13……………………..(4)
Multiplying equation (2) with 6 and equation (3) with 4;
18x – 12y + 24z = 222
− 16x + 12y − 24z =− 212
------------------------------------
2x = 10
x = 5
Substituting the value of x in equation (4)
x + 6y = -13
5 + 6y = -13
6y = -18
y= -3
Substituting the value of x and y in equation (1)
5- 3+ z = 6
2 + z = 6
z = 4

Solution.13:
Given:
(1/3) x + (2/5) y + (1/9) z = 1 ……………..(1)
(1/6) x - (3/5) y + (2/3) z = 10 ……………..(2)
(5/6) x + (4/5) y - (7/9) z = -6 …………….(3)
Multiplying equation (1) with 7 and adding with equation (3):
(7/3) x + (14/5) y + (7/9) z = 7
(5/6) x + (4/5) y - (7/9) z = -6
----------------------------------------
(19/6) x + (18/5) y = 1…………….(4)
Multiplying equation (2) with 1/6 and adding with equation (1):
(1/36) x – (1/10) y + (1/9) z = 5/3
(1/3) x + (2/5) y + (1/9) z = 1
- - - -
--------------------------------------
(-11/36) x – (1/5)y = 2/3…………….(5)
Multiplying 18 in equation (5);
(-11/2) x - (18/5)y = 12
(19/6) x + (18/5) y = 1
-------------------------------
(-14/6) x = 13
x = -39/7
(-11/36) (-39/7) – (1/5)y = 2/3
y = 5.175

(1/3) (-39/7) + (2/5) (5.175)+ (1/9) z = 1
z = 7.245
Solution.14:
Given:
C = Number of Cats.
D = Number of Dogs.
G= Number of Guinea pigs.
C + D +G = 254
G = D/3
C = D -40
(D/3) + D +(D-40) = 254
D + 3D +3D -120 = 762
7D = 762 + 120 = 882
D = 126
G = D/3 =126/3= 42
G = 42
C + 126 +42 = 254
C = 86
Solution.15:
Given:
U = United States,
C =China,
J = Japan.

U + C + J = 32.2…………..(1)
U = C +12
C = J +3.2
U = (J+ 3.2) +13
U = J +15.2
Substituting the value of U and C in equation 1
(J +15.2) + (J +3.2) + J = 32.2
3J = 32.2- 18.4
J = 4.6
U = J +15.2
U = 19.8
U + C + J = 32.2
19.8 + 4.6 +C =32.2
C = 7.8