MAS164: Semester 1 Mathematics Assignment - Function Analysis

This document presents a comprehensive solution to a mathematics assignment focusing on trigonometric functions and wave analysis. The assignment includes several parts, starting with the analysis of a trigonometric function f(t) = -1 + 4sin(π(t-1)/2), where the amplitude, period, maximum, and...Read More

Mathematics Assignment
Student Name:
Instructor Name:
Course Number:
7th May 2019

1 a) 4sin(1
2π(t-1))-1
Suppose f (t) =Asin[𝐵(𝑡 + 𝐶)] +D then
A=Amplitude and period=2𝜋
𝐵
Hence amplitude = 4
b) Period=
2𝜋
𝐵 = 2𝜋
𝜋
2
= 4
Period= 4
c) For f(t) to be either minimum or maximum then
rate of change of f(t) will be 0 i.e
𝑑
𝑑𝑥 (f(t)= f '(t)=0
𝑑
𝑑𝑥 (f(t)= 𝑑
𝑑𝑥 [4 sin (
1
2 𝜋(𝑡 − 1)) − 1]=0
= 2π cos(1
2 𝜋(𝑡 − 1))=0
Either 2π=0 or cos(1
2 𝜋(𝑡 − 1))=0
Taking cos(1
2 𝜋(𝑡 − 1))=0
cos−1 0 = 𝜋
2 ,3𝜋
2
(1
2 𝜋(𝑡 − 1))=𝜋
2 ,3𝜋
2
1
2 𝜋(𝑡 − 1) =𝜋
2 , (𝑡 − 1) =1, t=2
or 1
2 𝜋(𝑡 − 1) =3𝜋
2 ,(𝑡 − 1) =3, t=4
When t=2

When t=2 f(t) is maximum
f(t)= 4sin(1
2π(t-1))-1
f(2)= 4sin(1
2π(2-1))-1 f(2)= 4sin(1
2π(2-1))-1
=4sin(1
2π)-1 =4(1)-1=3
maximum value of f(t) =3
when t=4
When t=4 f(t) is minimum
f(t)= 4sin(1
2π(t-1))-1
f(4)= 4sin(1
2π(4-1))-1 f(4)= 4sin(1
2π(4-1))-1
f(4)= 4sin(3
2π)-1= 4(-1)-1=-5
minimum value of f(t) =-5
t 1 2 3
f ′(t)
2π 0 -2π
sign
positive zero negative
t 3 2 3
f ′(t)
-2π 0 2π
sign
positive zero negative

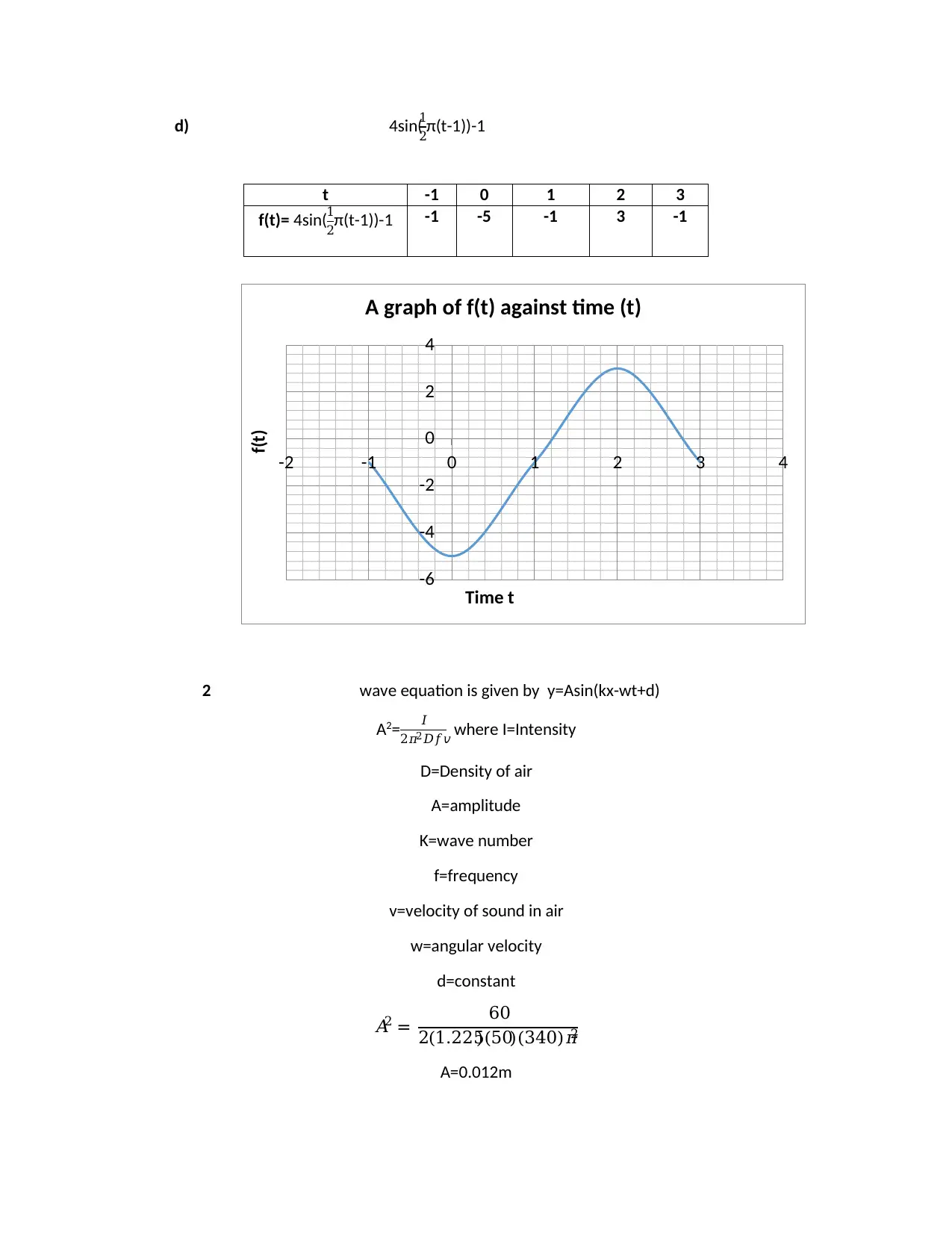
d) 4sin(
1
2π(t-1))-1
2 wave equation is given by y=Asin(kx-wt+d)
A2= 𝐼
2𝜋2𝐷𝑓𝑣 where I=Intensity
D=Density of air
A=amplitude
K=wave number
f=frequency
v=velocity of sound in air
w=angular velocity
d=constant
𝐴2 = 60
2(1.225)(50)(340)𝜋2
A=0.012m
t -1 0 1 2 3
f(t)= 4sin(1
2π(t-1))-1 -1 -5 -1 3 -1
-6
-4
-2
0
2
4
-2 -1 0 1 2 3 4
f(t)
Time t
A graph of f(t) against time (t)

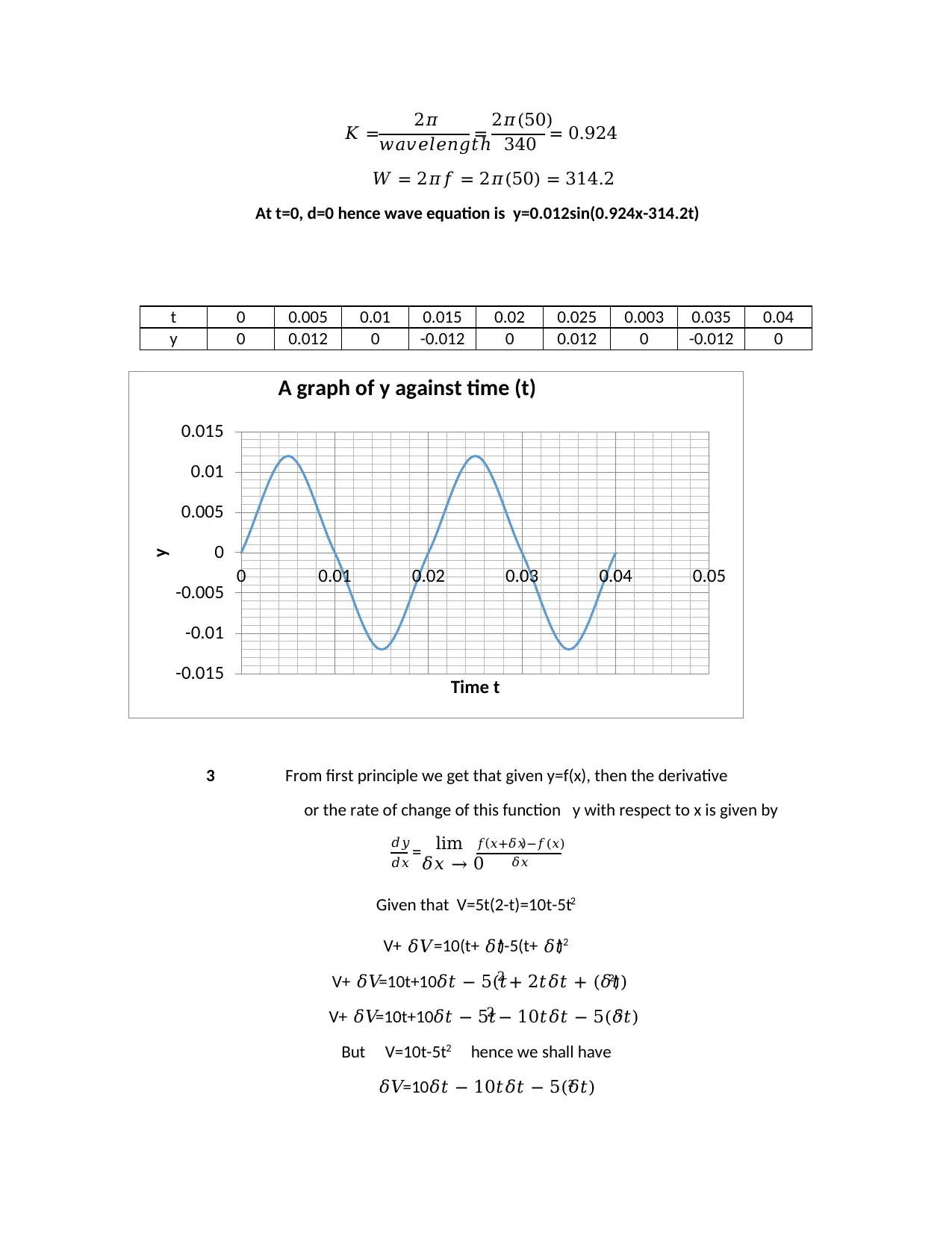
𝐾 = 2𝜋
𝑤𝑎𝑣𝑒𝑙𝑒𝑛𝑔𝑡ℎ
= 2𝜋(50)
340 = 0.924
𝑊 = 2𝜋𝑓 = 2𝜋(50) = 314.2
At t=0, d=0 hence wave equation is y=0.012sin(0.924x-314.2t)
3 From first principle we get that given y=f(x), then the derivative
or the rate of change of this function y with respect to x is given by
𝑑𝑦
𝑑𝑥 = lim
𝛿𝑥 → 0
𝑓(𝑥+𝛿𝑥)−𝑓(𝑥)
𝛿𝑥
Given that V=5t(2-t)=10t-5t2
V+ 𝛿𝑉=10(t+ 𝛿𝑡)-5(t+ 𝛿𝑡)2
V+ 𝛿𝑉=10t+10𝛿𝑡 − 5(𝑡2 + 2𝑡𝛿𝑡 + (𝛿𝑡)2)
V+ 𝛿𝑉=10t+10𝛿𝑡 − 5𝑡2 − 10𝑡𝛿𝑡 − 5(𝛿𝑡)2
But V=10t-5t2 hence we shall have
𝛿𝑉=10𝛿𝑡 − 10𝑡𝛿𝑡 − 5(𝛿𝑡)2
t 0 0.005 0.01 0.015 0.02 0.025 0.003 0.035 0.04
y 0 0.012 0 -0.012 0 0.012 0 -0.012 0
-0.015
-0.01
-0.005
0
0.005
0.01
0.015
0 0.01 0.02 0.03 0.04 0.05
y
Time t
A graph of y against time (t)

𝛿𝑉
𝛿𝑡 =10𝛿𝑡−10𝑡𝛿𝑡−5(𝛿𝑡)2
𝛿𝑡
𝛿𝑉
𝛿𝑡 =𝛿𝑡(10−10𝑡−5𝛿𝑡)
𝛿𝑡 =(10 − 10𝑡 − 5𝛿𝑡)
Therefore 𝑑𝑉
𝑑𝑡 = lim
𝛿𝑥 →0
(10 − 10𝑡 − 5𝛿𝑡)
𝑑𝑉
𝑑𝑡 =10-10t
Thus the rate of change of water 𝒅𝑽
𝒅𝒕 =10-10t
4 f(x)=x2-1
f(x) + 𝛿𝑓(𝑥)=(x+𝛿𝑥)2-1
f(x) + 𝛿𝑓(𝑥)=(x2+2𝑥𝛿𝑥 + (𝛿𝑥)2-1
But f(x)=x2-1 hence we shall have
𝛿𝑓(𝑥)=2𝑥𝛿𝑥 + (𝛿𝑥)2
= 𝛿𝑓(𝑥)
𝛿𝑥 =2𝑥𝛿𝑥+(𝛿𝑥)2
𝛿𝑥
= 𝑑
𝑑𝑥(f(x)=f'(x)= 2𝑥 + 𝛿𝑥
= f'(x)= lim
𝛿𝑥 →0
(2𝑥 + 𝛿𝑥)
= f'(x)= 2𝑥
When x=3 , f'(3)=2(3)=6=gradient
When x=3 , f(x)=32-1=8
The tangent (straight line) passes through (3,8)
and has a gradient of 6 at x=3.
The equation of the tangent can be found as follows
𝑦−8
𝑥−3=6
y-8=6(x-3)

y-8=6x-18
y=6x-10
The tangent to the graph has the equation y=6x-10