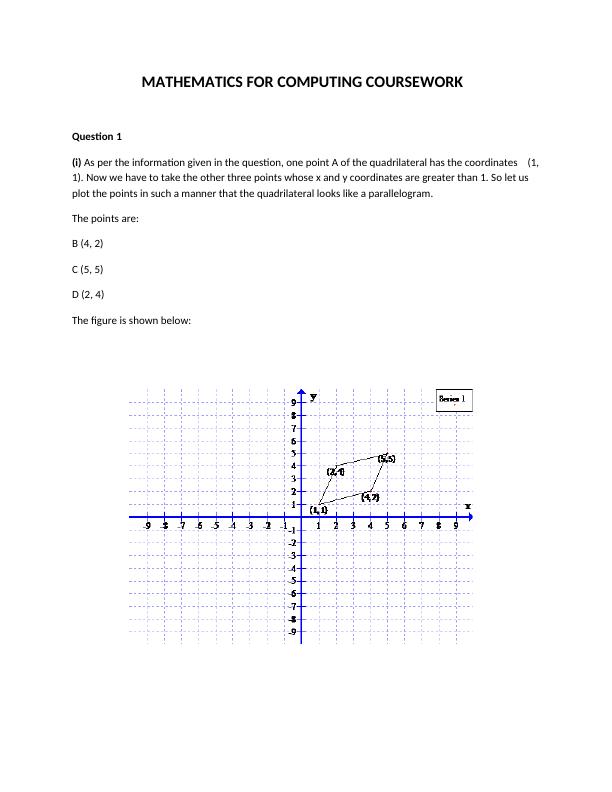
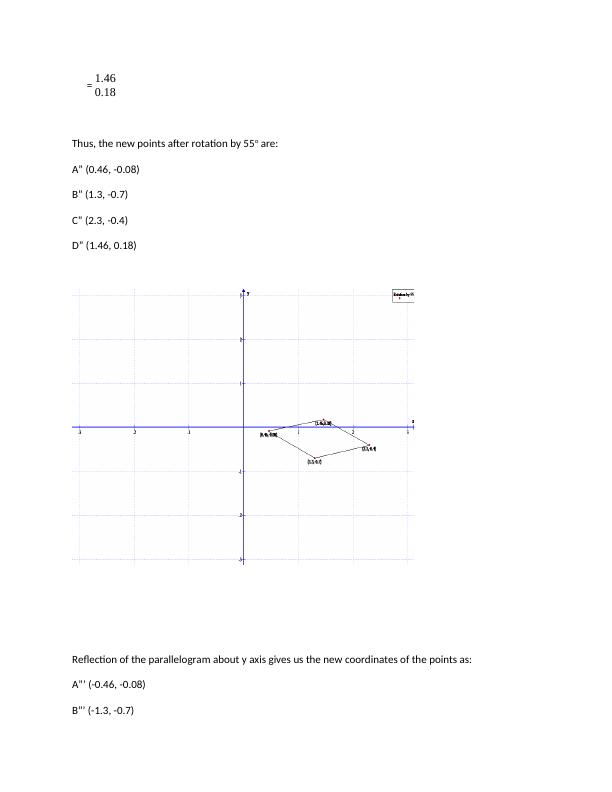
Ask a question from expert
Mathematics for Computing Coursework
15 Pages1768 Words204 Views
Added on 2019-10-01
About This Document
The Mathematics for Computing coursework includes solutions for questions on quadrilateral, matrix, probability, regression line, and more. The coursework covers topics such as calculating slope, midpoints, scaling down matrix, rotating points, Cramer's rule, frequency table, histogram, coefficient of correlation, regression line, Poisson distribution, and hypergeometric distribution.
Mathematics for Computing Coursework
Added on 2019-10-01
BookmarkShareRelated Documents
End of preview
Want to access all the pages? Upload your documents or become a member.
Solutions to the Fundamental Problems-Mechanical Engineering
|9
|700
|24