Mathematics for Construction

This document provides study material and solved assignments for Mathematics for Construction. It covers topics such as equations of vibration, vector equations, cost functions, and more. The document includes scenarios with detailed solutions and explanations.

Running head: MATHEMATICS FOR CONSTRUCTION
MATHEMATICS FOR CONSTRUCTION
Name of the Student
Name of the University
Author Note

1MATHEMATICS FOR CONSTRUCTION
Scenario 1:
Given equations of vibration,
x1=3.25 sin(100 πt+ 2 π
9 ¿)¿
x2=4.44 sin(100 πt− 2 π
5 ¿) ¿
i. amplitude of x1 = 3.25, amplitude of x2 = 4.44
phase of x1 = 2 π
9 ,phase of x2 = −2 π
5
frequency of x1 = 100 π /2 π = 50 Hz.
Hence, time period of x1 = 1/50 = 0.02 secs.
frequency of x2 = 100 π /2 π = 50 Hz.
Hence, time period of x2 = 1/50 = 0.02 secs.
ii. Maximum displacement of x1 = 3.25
Hence, 3.25 sin(100 πt+ 2 π
9 ¿)=3.25 ¿
 sin(100 πt + 2 π
9 ¿)=1 ¿
 100πt + 2 π
9 = arcsin(1)
 100πt + 2 π
9 = π/2
 100 πt = 5π/18
 t = 5/1800 = 0.0027 secs.

2MATHEMATICS FOR CONSTRUCTION
Hence, maximum amplitude of vibration is produced from machine 1 at time t = 0.0027 secs.
Similarly,
4.44 sin(100 πt− 2 π
5 ¿)=4.44 ¿
 100 πt = π
2 + 2 π
5 = 9 π
10
 t = 9/1000 = 0.009 secs.
Hence, the vibration of machine 2 reaches maximum amplitude at time t = 0.009 secs.
iii. The time at which the vibration reaches to a displacement of -2 mm is found by the
following equations.
x1=3.25 sin(100 πt+ 2 π
9 ¿)¿ = -2
x2=4.44 sin(100 πt− 2 π
5 ¿)¿ = -2
3.25 sin(100 πt+ 2 π
9 ¿)¿ = -2
 sin(100 πt + 2 π
9 ¿)¿ = -2/3.25
 100 πt + 2 π
9 = arcsin(-2/3.25)
 100 πt + 2 π
9 = π + 0.66287
 100 πt = 3.1063
 t=¿0.00988 secs.
Hence, vibration of machine 1 reaches -2 mm of displacement at time t = 0.00988 secs.
4.44 sin(100 πt− 2 π
5 ¿)¿ = -2

3MATHEMATICS FOR CONSTRUCTION
 sin(100 πt − 2 π
5 ¿)¿ = -2/4.44
 100 πt− 2 π
5 = arcsin(-2/4.44)
 100 πt = 4.8655
 t=¿0.01548 secs.
Hence, vibration of machine 2 reaches -2 mm at time t = 0.01548 secs.
iv. x1=3.25 sin(100 πt+ 2 π
9 ¿)¿
= 3.25(sin(100 πt)cos( 2 π
9 ¿+ cos ( 100 πt )∗sin ( 2 π
9 )¿
= 2.49sin(100πt) + 2.089cos ( 100 πt )
Hence, for x1 A = 2.49, B = 2.089
Similarly,
x2=4.44 sin(100 πt− 2 π
5 ¿) ¿
= 4.44(sin(100 πt ¿ cos (2 π
5 ) – cos(100 πt ¿∗sin ( 2 π
5 )¿
= 1.372sin( 100 πt ¿ – 4.223cos(100 πt ¿
Hence, for x2 A = 1.372 and B = -4.223
v. Now, from the above result
x1 + x2 = 2.49sin(100 πt) + 2.089cos ( 100 πt ) + 1.372sin( 100 πt ¿ – 4.223cos(100 πt ¿
= 3.862sin(100 πt) – 2.134cos(100 πt ¿
Rcos(theta) = 3.862 and Rsin(theta) = -2.134
tan(theta) = -2.134/3.862 = -0.55256
 theta = arctan(-0.55256) = -0.50481 rad
Hence, R = 3.862/cos(-0.50481) = 4.41237
Hence, x1 + x2 = 4.41237sin(100 πt−0.50481¿

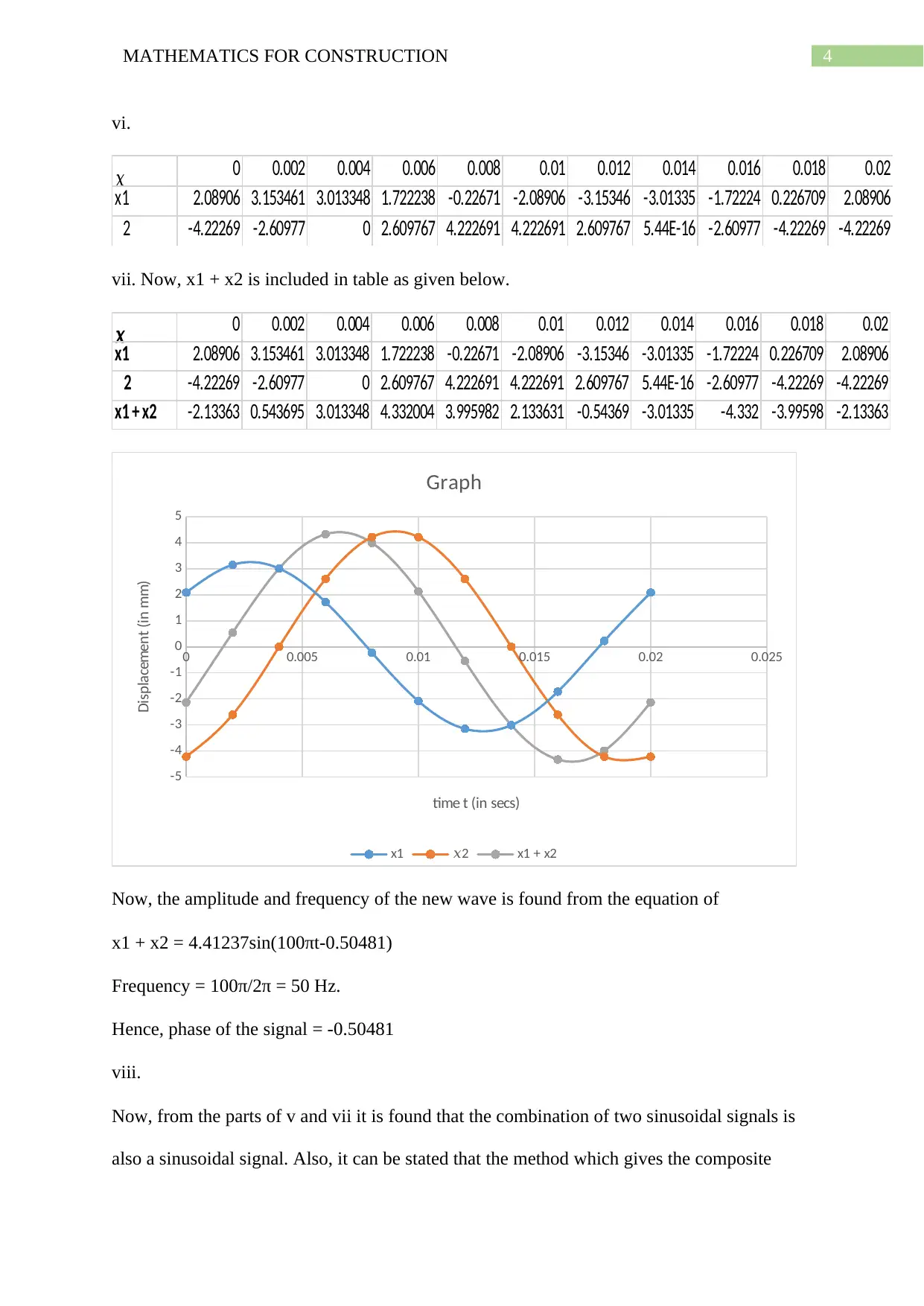
4MATHEMATICS FOR CONSTRUCTION
vi.𝒕
0 0.002 0.004 0.006 0.008 0.01 0.012 0.014 0.016 0.018 0.02
x1 2.08906 3.153461 3.013348 1.722238 -0.22671 -2.08906 -3.15346 -3.01335 -1.72224 0.226709 2.08906
𝑥
2 -4.22269 -2.60977 0 2.609767 4.222691 4.222691 2.609767 5.44E-16 -2.60977 -4.22269 -4.22269
vii. Now, x1 + x2 is included in table as given below.𝒕
0 0.002 0.004 0.006 0.008 0.01 0.012 0.014 0.016 0.018 0.02
x1 2.08906 3.153461 3.013348 1.722238 -0.22671 -2.08906 -3.15346 -3.01335 -1.72224 0.226709 2.08906
𝑥
2 -4.22269 -2.60977 0 2.609767 4.222691 4.222691 2.609767 5.44E-16 -2.60977 -4.22269 -4.22269
x1 + x2 -2.13363 0.543695 3.013348 4.332004 3.995982 2.133631 -0.54369 -3.01335 -4.332 -3.99598 -2.13363
0 0.005 0.01 0.015 0.02 0.025
-5
-4
-3
-2
-1
0
1
2
3
4
5
Graph
x1 𝑥2 x1 + x2
time t (in secs)
Displacement (in mm)
Now, the amplitude and frequency of the new wave is found from the equation of
x1 + x2 = 4.41237sin(100πt-0.50481)
Frequency = 100π/2π = 50 Hz.
Hence, phase of the signal = -0.50481
viii.
Now, from the parts of v and vii it is found that the combination of two sinusoidal signals is
also a sinusoidal signal. Also, it can be stated that the method which gives the composite

5MATHEMATICS FOR CONSTRUCTION
signal x1 + x2 as sinusoidal signal is compound angle method.
Scenario 2
i.
The end points of vector ⃗ AB are A = (0,-40, 0), B = (40, 0,-20)
Hence, vector ⃗ AB = (40-0)i + (0+40)j + (-20 – 0)k = 40i + 40j -20k
The distance AB = √ ( 40−0 ) 2 + ( 0+ 40 ) 2 + ( −20−0 ) 2 = √ 1600+1600+400 = 60
ii.
BC is drilled in direction of vector 3i + 4j + k
Hence, angle between the sections AB and BC is given by,
cos ( θ )=( AB . BC)/(||AB||∗||BC||)
= ( 40 i+ 40 j−20 k ) ( 3i+4 j+k )
√ 402 +402+ ( −20 ) 2∗√ 32 +42+ 12 = ( 40 i+ 40 j−20 k ) (3i+4 j+k )
√ 402 +402+ ( −20 ) 2∗√ 32 +42+ 12 = 120+160−20
60∗ √ 26 =
0.8498
 θ = arccos(0.8498) = 0.55512.
Hence, the angle between the sections AB and BC is 0.55512 rad.
iii.
The vector equation of BC is given by,⃗
BC = (a-40)i + bj + 20k
Now, the vector BC is drilled in the direction 3i + 4j + k.
Hence, unit vector in direction 3i + 4j + k is⃗
^BC = ((a-40)i + bj + 20k)/|| 3i + 4j + k|| = ((a-40)i + bj + 20k)/ √26

6MATHEMATICS FOR CONSTRUCTION
Hence, by comparison
a-40 = 3 => a = 43 and b = 4.
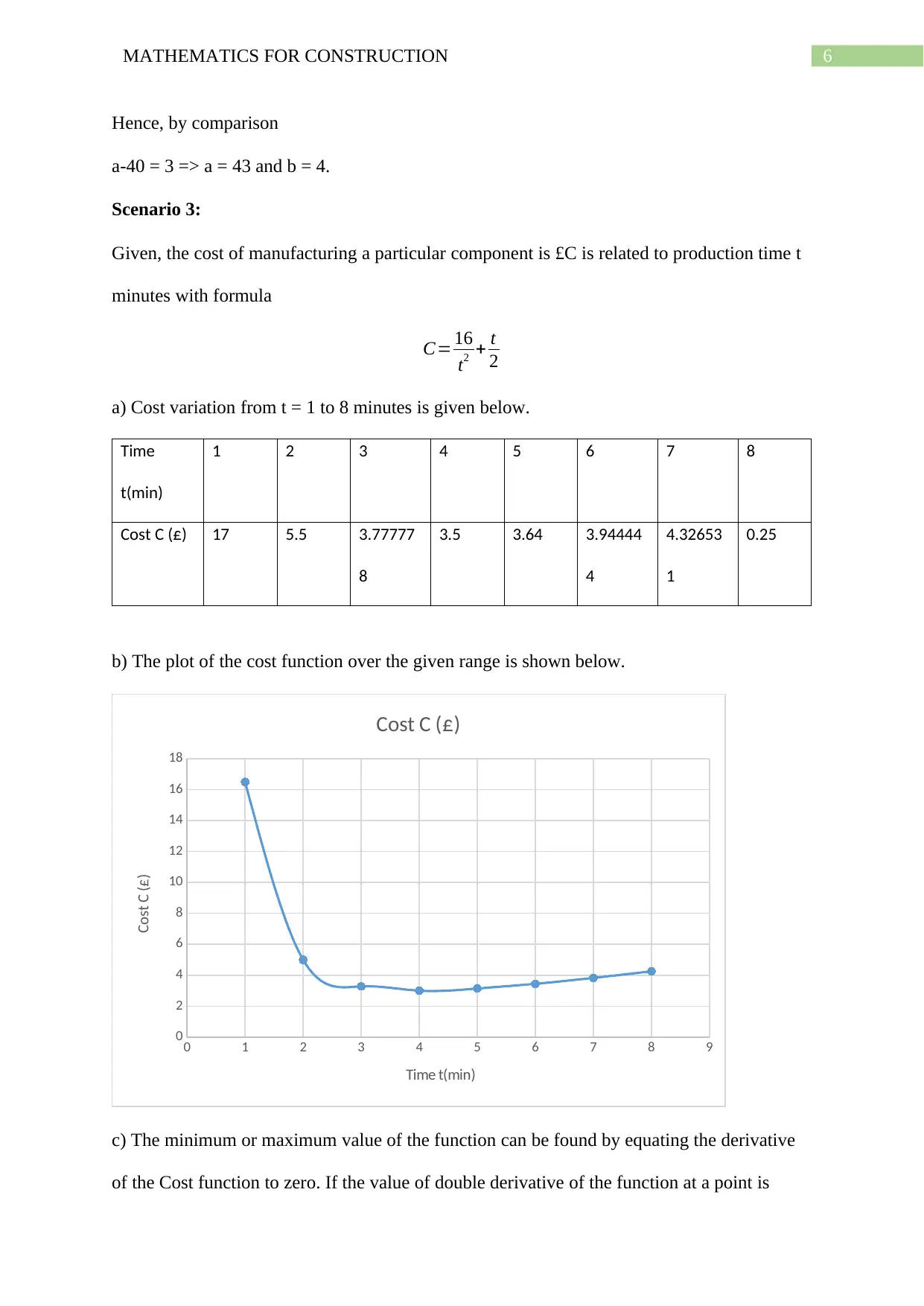
Scenario 3:
Given, the cost of manufacturing a particular component is £C is related to production time t
minutes with formula
C= 16
t2 + t
2
a) Cost variation from t = 1 to 8 minutes is given below.
Time
t(min)
1 2 3 4 5 6 7 8
Cost C (£) 17 5.5 3.77777
8
3.5 3.64 3.94444
4
4.32653
1
0.25
b) The plot of the cost function over the given range is shown below.
0 1 2 3 4 5 6 7 8 9
0
2
4
6
8
10
12
14
16
18
Cost C (£)
Time t(min)
Cost C (£)
c) The minimum or maximum value of the function can be found by equating the derivative
of the Cost function to zero. If the value of double derivative of the function at a point is

7MATHEMATICS FOR CONSTRUCTION
negative then in that point the function has a maximum and if the double derivative is
positive then in that point the function has a minimum.
d) C = 16
t2 + t
2
dC
dt =−32
t3 + 1
2 = 0
 −32
t3 + 1
2 = 0
 t^3/32 = 2
 t^3 = 64
 t = 4 secs
This t = 4 secs is the turning point of the cost function.
e)
d2 C
d t 2 =−96
t4
d2 C
d t2 ∨t=4 = -96/64 (negative value)
Hence, the function has a minimum in t = 4 secs.
Also from the graph of the cost function it is also evident that at this turning point the
function has a minimum. The minimum value of cost is C = £ 3.5.
f) The components should be manufactured in a cost effective way by producing the
components at the turning points where the cost function is minimum. In this case the
minimum value is at t= 4 secs.
g) Now, cost function is
C = 16/t + t^2/2
The critical point is found below.
dC
dt =0

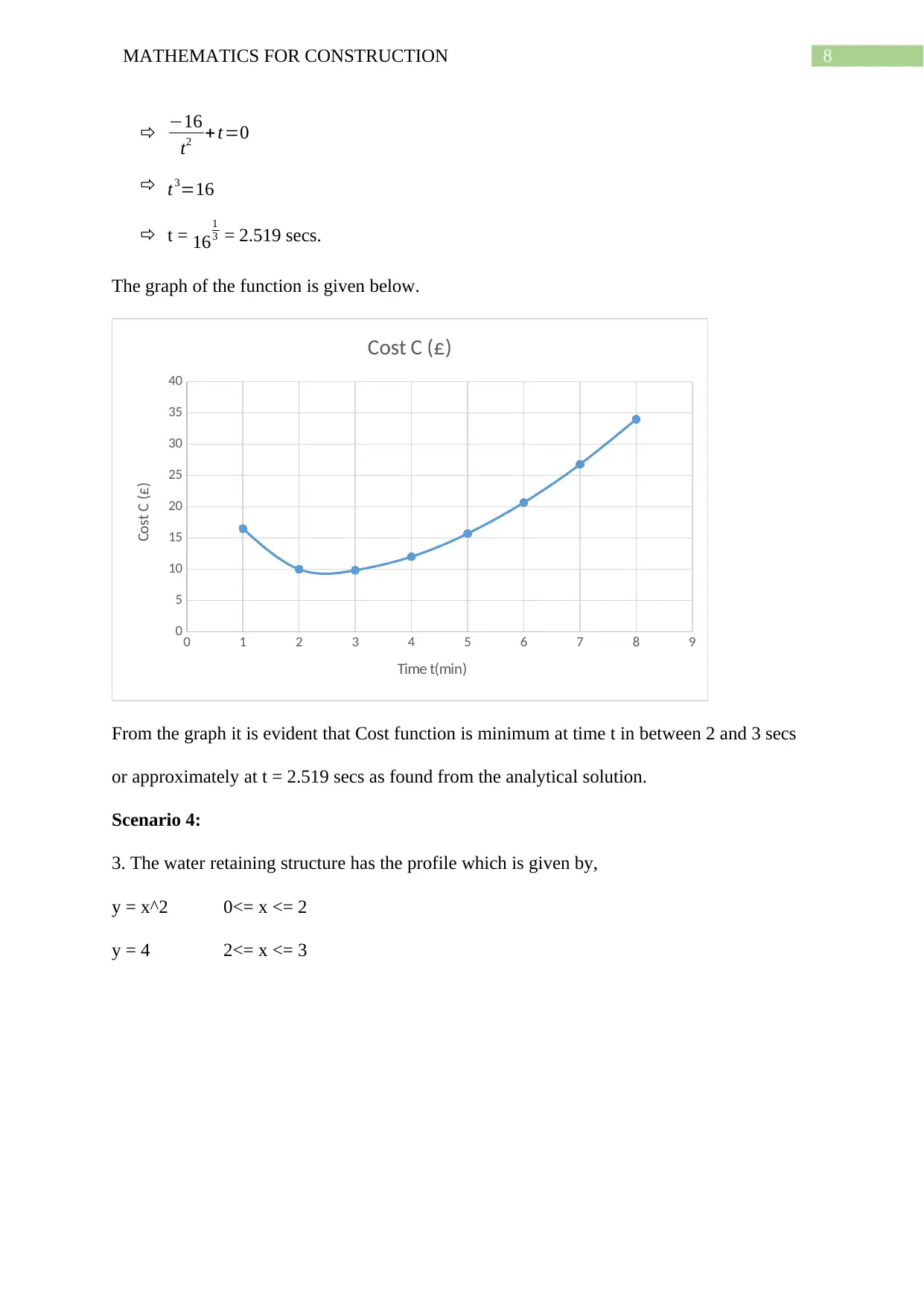
8MATHEMATICS FOR CONSTRUCTION
 −16
t2 +t=0
 t3=16
 t = 16
1
3 = 2.519 secs.
The graph of the function is given below.
0 1 2 3 4 5 6 7 8 9
0
5
10
15
20
25
30
35
40
Cost C (£)
Time t(min)
Cost C (£)
From the graph it is evident that Cost function is minimum at time t in between 2 and 3 secs
or approximately at t = 2.519 secs as found from the analytical solution.
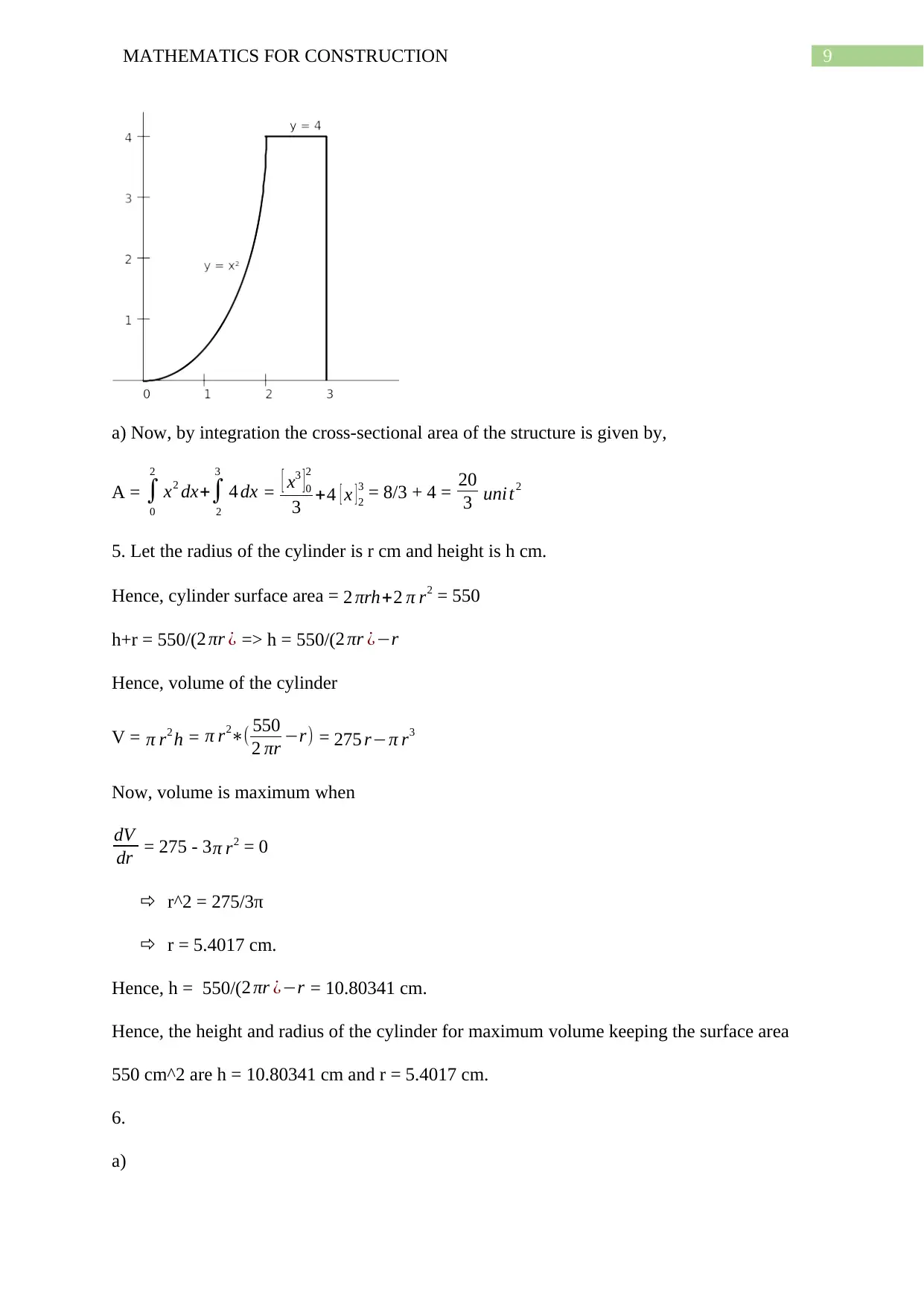
Scenario 4:
3. The water retaining structure has the profile which is given by,
y = x^2 0<= x <= 2
y = 4 2<= x <= 3

9MATHEMATICS FOR CONSTRUCTION
a) Now, by integration the cross-sectional area of the structure is given by,
A = ∫
0
2
x2 dx+∫
2
3
4 dx = [ x3 ] 0
2
3 +4 [ x ] 2
3 = 8/3 + 4 = 20
3 unit2
5. Let the radius of the cylinder is r cm and height is h cm.
Hence, cylinder surface area = 2 πrh+2 π r2 = 550
h+r = 550/(2 πr ¿ => h = 550/(2 πr ¿−r
Hence, volume of the cylinder
V = π r2 h = π r2∗( 550
2 πr −r) = 275 r−π r3
Now, volume is maximum when
dV
dr = 275 - 3π r2 = 0
 r^2 = 275/3π
 r = 5.4017 cm.
Hence, h = 550/( 2 πr ¿−r = 10.80341 cm.
Hence, the height and radius of the cylinder for maximum volume keeping the surface area
550 cm^2 are h = 10.80341 cm and r = 5.4017 cm.
6.
a)

10MATHEMATICS FOR CONSTRUCTION
Equation of circle
x^2 + y^2 = 25 => y^2 = 25 – x^2
Volume of solid revolution about x axis is given by,
V = ∫
a
b
π y2 dx = ∫
0
5
π ( 25−x2 ) dx (as radius of circle is 5 m and the first quadrant is rotated)
= π (25 [ x ]0
5 − [ x3 ] 0
5
3 ) = π (25∗5− 125
3 ) = 261.7994 c m3.
b) Now, the volume of the above hemisphere cut-off at 2 meters and 3 meters from plane
base or the limit of integration will be 2 to 3.
Hence,
V = V = ∫
a
b
π y2 dx = ∫
2
3
π ( 25−x2 ) dx = = π (25 [ x ]2
3 − [ x3 ] 2
3
3 ) = π (25−19
3 ) = 58.643 c m3.
7. The portion of the curve y = x(x-1) that lies under x-axis is inside x limit [0,1] obtained
from the solutions of equation,
x(x-1) = 0
Hence, the volume of revolution of that part about x axis will be,
V = π∫
0
1
y2 dx = π∫
0
1
x2 ( x−1 ) 2 dx = π/30 unit3.

11MATHEMATICS FOR CONSTRUCTION