Mathematics for IT
VerifiedAdded on 2023/06/07
|19
|2062
|361
AI Summary
This article covers topics such as trigonometric functions, coordinate geometry, complex numbers, and matrices. It includes solved problems and examples for each topic.
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

MATHEMATICS FOR IT
[Author Name(s), First M. Last, Omit Titles and Degrees]
[Institutional Affiliation(s)]
[Author Name(s), First M. Last, Omit Titles and Degrees]
[Institutional Affiliation(s)]
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

Question One: Trigonometric Functions; Angles
(a)
(i) 7/sin 35=10/sin A
Sin A= (sin 35*10)/7
A=55⁰
(ii) s2 =72+102
s2=49+100
s2=149
s= √ 149=12.21 cm
(b) For a small Ɵ, a triangle as shown below is noticed
i. With a small value of Ɵ, the opposite angle i.e. a is very small with the adjacent angle i.e. b as
well as the hypotenuse (h) being relatively large. Hence,
Sin Ɵ=a/h ≈ 0
tan Ɵ=a/b≈ 0
(a)
(i) 7/sin 35=10/sin A
Sin A= (sin 35*10)/7
A=55⁰
(ii) s2 =72+102
s2=49+100
s2=149
s= √ 149=12.21 cm
(b) For a small Ɵ, a triangle as shown below is noticed
i. With a small value of Ɵ, the opposite angle i.e. a is very small with the adjacent angle i.e. b as
well as the hypotenuse (h) being relatively large. Hence,
Sin Ɵ=a/h ≈ 0
tan Ɵ=a/b≈ 0

besides, it should be noticed that h and b are almost the same height with h being only slightly
longer and hence
cos Ɵ=b/h≈ 1
b≈h and hence a/h≈a/b and thus sin Ɵ≈tan Ɵ
ii. When the C=9⁰;
10
sin 81 = AB
sin 9
AB= 10 sin 9
sin 81 =4.173 units
10
sin 81 = AC
sin 90
AC= 10 sin 9 0
sin 81 =10.12 units
Question 2: Applications of Trigonometric Functions
(a) Scalene triangle. Neither of the sides nor the angles is equal
(b) a2 =b2+c2-2bc cos A
=202+302-2*30*20 cos 25
a=√212.4=14.57 units
(c) b
sin B = a
sin A
longer and hence
cos Ɵ=b/h≈ 1
b≈h and hence a/h≈a/b and thus sin Ɵ≈tan Ɵ
ii. When the C=9⁰;
10
sin 81 = AB
sin 9
AB= 10 sin 9
sin 81 =4.173 units
10
sin 81 = AC
sin 90
AC= 10 sin 9 0
sin 81 =10.12 units
Question 2: Applications of Trigonometric Functions
(a) Scalene triangle. Neither of the sides nor the angles is equal
(b) a2 =b2+c2-2bc cos A
=202+302-2*30*20 cos 25
a=√212.4=14.57 units
(c) b
sin B = a
sin A

30
sin B = 14.57
sin 25
sin B= 30 sin 25
14.57 =0.871
B=60.57⁰
(d) c
sin C = a
sin A
30
sin C = 14.57
sin 25
sin C= 20sin 25
14.57 =0.581
C=35.52⁰
(e) Area of the triangle
A= √s (s−a)(s−b)( s−c)
S=p/2= (20+30+14.57)/2=32.3
A= √ 32.3 (32.3−30)(32.3−20)(32.3−14.57)
√ 32.3× 2.3 ×12.3 ×17.73=127.28 sq. units
Question 3: Trigonometric Functions of Real Numbers
(a)
sin B = 14.57
sin 25
sin B= 30 sin 25
14.57 =0.871
B=60.57⁰
(d) c
sin C = a
sin A
30
sin C = 14.57
sin 25
sin C= 20sin 25
14.57 =0.581
C=35.52⁰
(e) Area of the triangle
A= √s (s−a)(s−b)( s−c)
S=p/2= (20+30+14.57)/2=32.3
A= √ 32.3 (32.3−30)(32.3−20)(32.3−14.57)
√ 32.3× 2.3 ×12.3 ×17.73=127.28 sq. units
Question 3: Trigonometric Functions of Real Numbers
(a)
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

(i)15⁰
π Radians=180⁰
15⁰= 15× π
180 =0.8333 π
(ii) 240⁰
π Radians =180⁰
240⁰= 240× π
180 =1.333 π
-425⁰
π Radians=180⁰
(iii)-425⁰=−425 × π
180 =-2.361π
(b) Conversion to degrees
(i) π
3
π=1800; π
3 = π
3 ×180 × 1
π =60⁰
(ii) 5 π
8
π=1800; 5 π
8 = 5 π
8 ×180 × 1
π =112.5⁰
π Radians=180⁰
15⁰= 15× π
180 =0.8333 π
(ii) 240⁰
π Radians =180⁰
240⁰= 240× π
180 =1.333 π
-425⁰
π Radians=180⁰
(iii)-425⁰=−425 × π
180 =-2.361π
(b) Conversion to degrees
(i) π
3
π=1800; π
3 = π
3 ×180 × 1
π =60⁰
(ii) 5 π
8
π=1800; 5 π
8 = 5 π
8 ×180 × 1
π =112.5⁰

(iii) −5 π
4
π=1800; −5 π
4 =−5 π
4 ×180 × 1
π =-225⁰
Question 4: Coordinate Geometry in two dimensions
(a) y=x2 +4 x−8
y=3 x−2
y=y; x2+4 x−8=3 x−2
x2−x−6=0
x= 1± √ 5
2 =1 ± 2.236
2
x=1.618∨−0.618
When x=1.618, y=3(1.618)-2=2.854 while when x=-0.618, y=3(-0.618)-2=-3.854. The
coordinates of intersection are thus (1.618, 2.854) and (-0.618, -3.854)
(ii) y=x2 +4 x−8; y=2 x−9
x2+ 4 x−8=2 x−9
x2+ 2 x +1=0
x= 1± √4−4
2 = 1± 0
2
x=0.5
4
π=1800; −5 π
4 =−5 π
4 ×180 × 1
π =-225⁰
Question 4: Coordinate Geometry in two dimensions
(a) y=x2 +4 x−8
y=3 x−2
y=y; x2+4 x−8=3 x−2
x2−x−6=0
x= 1± √ 5
2 =1 ± 2.236
2
x=1.618∨−0.618
When x=1.618, y=3(1.618)-2=2.854 while when x=-0.618, y=3(-0.618)-2=-3.854. The
coordinates of intersection are thus (1.618, 2.854) and (-0.618, -3.854)
(ii) y=x2 +4 x−8; y=2 x−9
x2+ 4 x−8=2 x−9
x2+ 2 x +1=0
x= 1± √4−4
2 = 1± 0
2
x=0.5

When x=0.5, y=2(0.5)-2=-1. The coordinates of intersection are thus (0.5, -1)
(b)
(i) y=x2−4 x +4−1; x2+ y2=9
y=y; x2−4 x+3= √ −x2+ 9
(x2−4 x+3)2=±(x¿ ¿2+ 9)¿
x2−x=0 ; x=1
But x2+ y2=9 ;1+ y2=9 ; y=2.828
The coordinates are (1, 2.828)
(ii) Coordinates are (1, 2.8) and (0,0)
m= y2− y1
x−x1
= 2.8−0=2.8
1−0
2.8= y −2.8
x−1 ; y=2.8x
Question 5: Coordinate Geometry in three dimensions
(i) Sphere
(ii)¿
¿
¿
(b)
(i) y=x2−4 x +4−1; x2+ y2=9
y=y; x2−4 x+3= √ −x2+ 9
(x2−4 x+3)2=±(x¿ ¿2+ 9)¿
x2−x=0 ; x=1
But x2+ y2=9 ;1+ y2=9 ; y=2.828
The coordinates are (1, 2.828)
(ii) Coordinates are (1, 2.8) and (0,0)
m= y2− y1
x−x1
= 2.8−0=2.8
1−0
2.8= y −2.8
x−1 ; y=2.8x
Question 5: Coordinate Geometry in three dimensions
(i) Sphere
(ii)¿
¿
¿
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Coordinates are (5, 5, -5); r= √25=5
(iii) No. The coordinates do not pass through the origin
(iv) )¿
Question 6: Complex Numbers
(a)
(i) ( 5−17 i ) +(17−24 i)
¿ ( 5−17i+17−24 i ) =5+17−17 i−24 i
¿ 22−41i
(ii) ( 5
4 + 1
3 i )−(2− 3
5 i)
¿ 5
4 + 1
3 i−2+ 3
5 i= 5
4 −2+ 1
3 i+ 3
5 i
¿− 3
4 + 14
15 i
(iii) ( 2−7 i ) ( 5+6 i ) =10+12 i−35 i−42 i2
¿ 10−23i+ 42=52−23 i
(iv) 2−7 i
5+6 i . 5−6 i
5−6 i =10−12i−35i+ 42i2
25−30 i+30 i−36 i2 =−32−47i
61
(b) As noticed from the definition of what complex number is:
z=(x1, y1)
(iii) No. The coordinates do not pass through the origin
(iv) )¿
Question 6: Complex Numbers
(a)
(i) ( 5−17 i ) +(17−24 i)
¿ ( 5−17i+17−24 i ) =5+17−17 i−24 i
¿ 22−41i
(ii) ( 5
4 + 1
3 i )−(2− 3
5 i)
¿ 5
4 + 1
3 i−2+ 3
5 i= 5
4 −2+ 1
3 i+ 3
5 i
¿− 3
4 + 14
15 i
(iii) ( 2−7 i ) ( 5+6 i ) =10+12 i−35 i−42 i2
¿ 10−23i+ 42=52−23 i
(iv) 2−7 i
5+6 i . 5−6 i
5−6 i =10−12i−35i+ 42i2
25−30 i+30 i−36 i2 =−32−47i
61
(b) As noticed from the definition of what complex number is:
z=(x1, y1)

w=(x2, y2) in which
z+w=(x1, y1) + (x2, y2)
=(x1+y1+x2+y2)
=(x2, y2) + (x1, y1)
=w+z
Question 7: Polar, trigonometric and exponential forms of complex numbers
(a)Converting into polar form
2+4i
Suppose z=a+ bi
The z may be written in polar form as
z=r (cos Ɵ+ i sin Ɵ)
Where r= √a2 +b2∧Ɵ=arctan ( b
a )
For this question: z= 2+4i
Hence: a=2, b=4
Thus: r=√ 22+ 42=√20
z+w=(x1, y1) + (x2, y2)
=(x1+y1+x2+y2)
=(x2, y2) + (x1, y1)
=w+z
Question 7: Polar, trigonometric and exponential forms of complex numbers
(a)Converting into polar form
2+4i
Suppose z=a+ bi
The z may be written in polar form as
z=r (cos Ɵ+ i sin Ɵ)
Where r= √a2 +b2∧Ɵ=arctan ( b
a )
For this question: z= 2+4i
Hence: a=2, b=4
Thus: r=√ 22+ 42=√20

And Ɵ=arctan ( 4
2 )≅0.46
Hence the polar form of 2+4i is approximately 4.47(cos (0.46) + i sin (0.46))
9+9i
Suppose z=a+ bi
The z may be written in polar form as
z=r (cos Ɵ+ i sin Ɵ)
Where r= √a2 +b2∧Ɵ=arctan ( b
a )
For this question: z= 9+9i
Hence: a=9, b=9
Thus: r=√ 92 +92=√162
And Ɵ=arctan ( 9
9 )≅ 0.79
Hence the polar form of 9+9i is approximately 12.73(cos (0.79) + i sin (0.79))
-7+2i
Suppose z=a+ bi
The z may be written in polar form as
z=r (cos Ɵ+ i sin Ɵ)
2 )≅0.46
Hence the polar form of 2+4i is approximately 4.47(cos (0.46) + i sin (0.46))
9+9i
Suppose z=a+ bi
The z may be written in polar form as
z=r (cos Ɵ+ i sin Ɵ)
Where r= √a2 +b2∧Ɵ=arctan ( b
a )
For this question: z= 9+9i
Hence: a=9, b=9
Thus: r=√ 92 +92=√162
And Ɵ=arctan ( 9
9 )≅ 0.79
Hence the polar form of 9+9i is approximately 12.73(cos (0.79) + i sin (0.79))
-7+2i
Suppose z=a+ bi
The z may be written in polar form as
z=r (cos Ɵ+ i sin Ɵ)
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

Where r= √a2 +b2∧Ɵ=arctan ( b
a )
For this question: z= -7+2i
Hence: a=-7, b=2
Thus: r=√ (−7)2 +22=√ 53
And Ɵ=π −arctan ( 7
2 )≅ 3.142−1.29
Hence the polar form of -7+2i is approximately 7.28(cos (1.852) + i sin (1.852))
(b) Conversion to trigonometric form
(2 – 4𝑖)
z=a+bi=|z| (cos Ɵ)+i sin Ɵ); |z|= √ a2 +b2 where z=a+bi
|z|=√ 42+ 22=2√5
Ɵ=arctan ( 4
2 )≅0.46
2 √ 5 ( cos 0.46 ) +¿
9+9i
z=a+bi=|z| (cos Ɵ)+i sin Ɵ); |z|= √ a2 +b2 where z=a+bi
|z|=√ 92 +92=9√2
a )
For this question: z= -7+2i
Hence: a=-7, b=2
Thus: r=√ (−7)2 +22=√ 53
And Ɵ=π −arctan ( 7
2 )≅ 3.142−1.29
Hence the polar form of -7+2i is approximately 7.28(cos (1.852) + i sin (1.852))
(b) Conversion to trigonometric form
(2 – 4𝑖)
z=a+bi=|z| (cos Ɵ)+i sin Ɵ); |z|= √ a2 +b2 where z=a+bi
|z|=√ 42+ 22=2√5
Ɵ=arctan ( 4
2 )≅0.46
2 √ 5 ( cos 0.46 ) +¿
9+9i
z=a+bi=|z| (cos Ɵ)+i sin Ɵ); |z|= √ a2 +b2 where z=a+bi
|z|=√ 92 +92=9√2

Ɵ=arctan ( 9
9 ) ≅0.79
9 √2 ( cos 0.79 ) +¿
-7+2i
z=a+bi=|z| (cos Ɵ)+i sin Ɵ); |z|= √ a2 +b2 where z=a+bi
|z|=√ (−7)2 +22=2√13.25
Ɵ=π −arctan ( 7
2 ) ≅ 1.852
2 √13.25 ( cos 1.852 ) +¿
(c) Exponential form
2+4i
∝= 2
4 =0.5 radians=28.6 degrees
Ɵ= 0.5
r = √22 +42=√20=4.472
=4.472 e0.5 j
9+9i
∝= 9
9 =1 radians=57.3 degrees
9 ) ≅0.79
9 √2 ( cos 0.79 ) +¿
-7+2i
z=a+bi=|z| (cos Ɵ)+i sin Ɵ); |z|= √ a2 +b2 where z=a+bi
|z|=√ (−7)2 +22=2√13.25
Ɵ=π −arctan ( 7
2 ) ≅ 1.852
2 √13.25 ( cos 1.852 ) +¿
(c) Exponential form
2+4i
∝= 2
4 =0.5 radians=28.6 degrees
Ɵ= 0.5
r = √22 +42=√20=4.472
=4.472 e0.5 j
9+9i
∝= 9
9 =1 radians=57.3 degrees

Ɵ=1
r = √92+92=√ 162=12.73
=12.73 e1 j
-7+2i
∝= 2
7 =0.286 radians=16.4 degrees
Ɵ=π−1.29=1.852
r = √72+22=√56=7.28
=7.28 e1.852 j
Question 8: Matrices
(a) A+C= (−2 4
5 7 ) + ( 2 2
3 4 ) =( 0 6
8 11 )
(b) B-D= (11 4 15
5 6 8
3 5 2 )− (1 6 5
7 2 4
8 9 3 )= ( 10 −2 10
−2 4 4
−5 −4 −1 )
(c) A.C= (−2 4
5 7 )∗(2 2
3 4 )= ( 8 12
31 38 )
(d) B.D= (11 4 15
5 6 8
3 5 2 )× (1 6 5
7 2 4
8 9 3 )=
(159 209 116
111 114 73
54 46 41 )
r = √92+92=√ 162=12.73
=12.73 e1 j
-7+2i
∝= 2
7 =0.286 radians=16.4 degrees
Ɵ=π−1.29=1.852
r = √72+22=√56=7.28
=7.28 e1.852 j
Question 8: Matrices
(a) A+C= (−2 4
5 7 ) + ( 2 2
3 4 ) =( 0 6
8 11 )
(b) B-D= (11 4 15
5 6 8
3 5 2 )− (1 6 5
7 2 4
8 9 3 )= ( 10 −2 10
−2 4 4
−5 −4 −1 )
(c) A.C= (−2 4
5 7 )∗(2 2
3 4 )= ( 8 12
31 38 )
(d) B.D= (11 4 15
5 6 8
3 5 2 )× (1 6 5
7 2 4
8 9 3 )=
(159 209 116
111 114 73
54 46 41 )
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
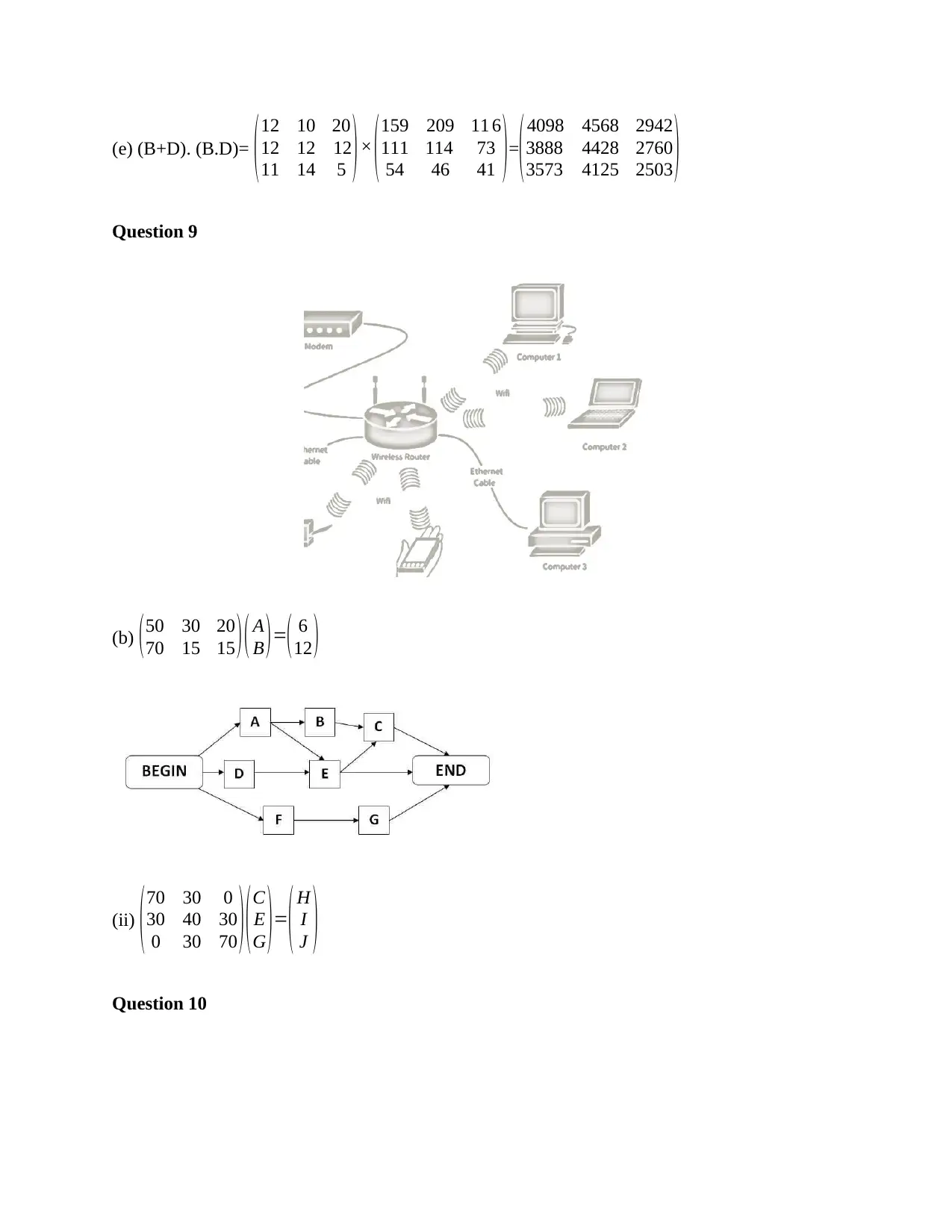
(e) (B+D). (B.D)= (12 10 20
12 12 12
11 14 5 )× (159 209 11 6
111 114 73
54 46 41 )=
( 4098 4568 2942
3888 4428 2760
3573 4125 2503 )
Question 9
(b) (50 30 20
70 15 15 )( A
B )=( 6
12 )
(ii) (70 30 0
30 40 30
0 30 70 )(C
E
G )=
( H
I
J )
Question 10
12 12 12
11 14 5 )× (159 209 11 6
111 114 73
54 46 41 )=
( 4098 4568 2942
3888 4428 2760
3573 4125 2503 )
Question 9
(b) (50 30 20
70 15 15 )( A
B )=( 6
12 )
(ii) (70 30 0
30 40 30
0 30 70 )(C
E
G )=
( H
I
J )
Question 10

( 2 −5 9
−1 3 −7
6 −8 4 )( x
y
z )=
( 37
−31
8 )
AX=B
X=A-1B
The first step is to find the inverse of the matrix
Calculating the inverse of matrix A
[ 2 −5 9
−1 3 −7
6 −8 4 ]−1
=
[−11
3
−13
3
2
3
−19
6
−23
6
5
12
−5
6
−7
6
1
12 ] [ 37
−31
8 ]= [4
5
6 ]
x
y
z
= [4
5
6 ]
Question 11
(i) A
→
+B
→
=
−6
2 + 4
8= 2
10
(ii) C
→
−D
→
=
5
7+−8
−3= (−3
4 )
(iii) B
→
× C
→
=( 4
8 ) × ( 5
7 ) =( 20
40 )
(iv) A
→
× D
→
=(−6
2 ) × (−8
3 ) =( 48
−16 )
−1 3 −7
6 −8 4 )( x
y
z )=
( 37
−31
8 )
AX=B
X=A-1B
The first step is to find the inverse of the matrix
Calculating the inverse of matrix A
[ 2 −5 9
−1 3 −7
6 −8 4 ]−1
=
[−11
3
−13
3
2
3
−19
6
−23
6
5
12
−5
6
−7
6
1
12 ] [ 37
−31
8 ]= [4
5
6 ]
x
y
z
= [4
5
6 ]
Question 11
(i) A
→
+B
→
=
−6
2 + 4
8= 2
10
(ii) C
→
−D
→
=
5
7+−8
−3= (−3
4 )
(iii) B
→
× C
→
=( 4
8 ) × ( 5
7 ) =( 20
40 )
(iv) A
→
× D
→
=(−6
2 ) × (−8
3 ) =( 48
−16 )
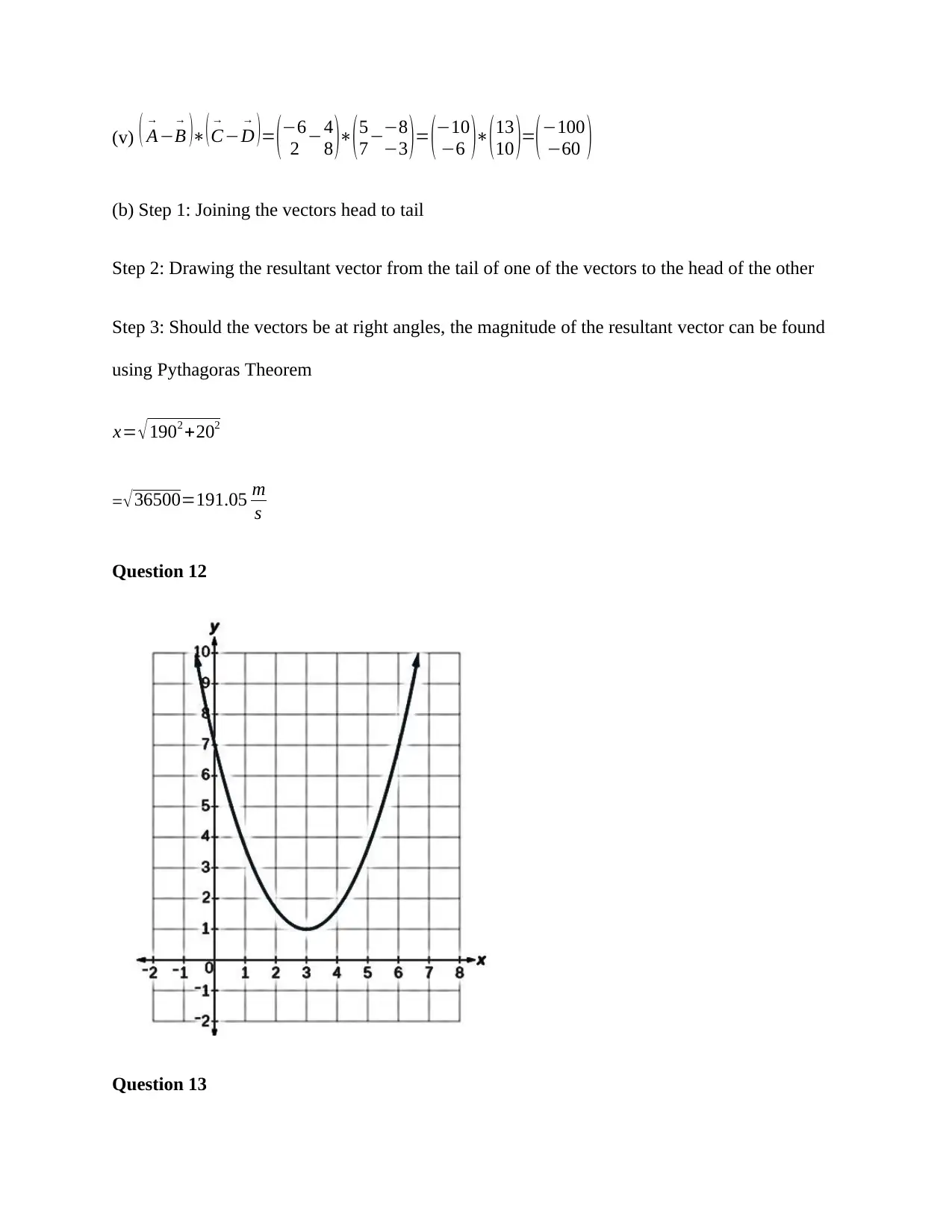
(v) ( A
→
−B
→
)∗( C
→
−D
→
)= (−6
2 −4
8 )∗( 5
7−−8
−3 )= (−10
−6 )∗( 13
10 )=( −100
−60 )
(b) Step 1: Joining the vectors head to tail
Step 2: Drawing the resultant vector from the tail of one of the vectors to the head of the other
Step 3: Should the vectors be at right angles, the magnitude of the resultant vector can be found
using Pythagoras Theorem
x= √ 1902 +202
=√36500=191.05 m
s
Question 12
Question 13
→
−B
→
)∗( C
→
−D
→
)= (−6
2 −4
8 )∗( 5
7−−8
−3 )= (−10
−6 )∗( 13
10 )=( −100
−60 )
(b) Step 1: Joining the vectors head to tail
Step 2: Drawing the resultant vector from the tail of one of the vectors to the head of the other
Step 3: Should the vectors be at right angles, the magnitude of the resultant vector can be found
using Pythagoras Theorem
x= √ 1902 +202
=√36500=191.05 m
s
Question 12
Question 13
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

Converting complex number to exponential
-3.7997-9.25i
∝= 3.7997
9.25 =−1.96 radians=28.6 degrees
Ɵ=−1.96
r = √ (−3.997)2 +9.2=√100.05=10.002
=10.002 e−1.96 j
Question 14
Denominator: (1+2i)(3-4i)(5+6i)
=(1+2i)(3-4i)=3+2i-8i2=3+2i+8
=11+2i
(11+2i) (5+6i)=55+76i+12i2=55+76i-12
=43-76i
Numerator: (7-8i)(9+10i)=63-2i-80i2=143-2i
(143-2i)(11-12i)=1573-1738i+24i2=1549-1738i
N/D=(43-76i)/(1549-1738i)
¿ (43−76 i)
(1549−1738i) . (1549+1738i)
(1549+1738i)=198695−194738i
5420045
-3.7997-9.25i
∝= 3.7997
9.25 =−1.96 radians=28.6 degrees
Ɵ=−1.96
r = √ (−3.997)2 +9.2=√100.05=10.002
=10.002 e−1.96 j
Question 14
Denominator: (1+2i)(3-4i)(5+6i)
=(1+2i)(3-4i)=3+2i-8i2=3+2i+8
=11+2i
(11+2i) (5+6i)=55+76i+12i2=55+76i-12
=43-76i
Numerator: (7-8i)(9+10i)=63-2i-80i2=143-2i
(143-2i)(11-12i)=1573-1738i+24i2=1549-1738i
N/D=(43-76i)/(1549-1738i)
¿ (43−76 i)
(1549−1738i) . (1549+1738i)
(1549+1738i)=198695−194738i
5420045

Question 15
(−2 −5 5
−2 3 −7
6 −2 1 )(x
y
z )=
( 31
−49
21 )
AX=B
X=A-1B
The first step is to find the inverse of the matrix
Calculating the inverse of matrix A
[−2 −5 5
−2 3 −7
6 −2 1 ]1
=
[ −11
152
−5
152
−5
36
−5
19
−4
19
−3
19
−7
76
−17
76
−2
19 ] [ 31
−49
21 ]= ( 3.5
1.1
19.8 )
( x
y
z )= ( 3.5
1.1
19.8 )
(−2 −5 5
−2 3 −7
6 −2 1 )(x
y
z )=
( 31
−49
21 )
AX=B
X=A-1B
The first step is to find the inverse of the matrix
Calculating the inverse of matrix A
[−2 −5 5
−2 3 −7
6 −2 1 ]1
=
[ −11
152
−5
152
−5
36
−5
19
−4
19
−3
19
−7
76
−17
76
−2
19 ] [ 31
−49
21 ]= ( 3.5
1.1
19.8 )
( x
y
z )= ( 3.5
1.1
19.8 )

References
AbuEloun, N. N., & Naser, S. S. A. (2017). Mathematics intelligent tutoring system
Dymond, J. H., Marsh, K. N., Wilhoit, R. C., & Frenkel, M. D. (2016). Virial Coefficients of
Mixtures (No. Virial Coefficients of Mixtures)
AbuEloun, N. N., & Naser, S. S. A. (2017). Mathematics intelligent tutoring system
Dymond, J. H., Marsh, K. N., Wilhoit, R. C., & Frenkel, M. D. (2016). Virial Coefficients of
Mixtures (No. Virial Coefficients of Mixtures)
1 out of 19
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.




