Mathematics Questions

This document contains a set of mathematics questions covering topics like calculations, simplifications, equations, percentages, and more. It provides step-by-step solutions and explanations for each question. The subjects covered include algebra, arithmetic, and statistics. The document is suitable for students studying mathematics at the college level.

MATHEMATICS
QUESTIONS

TABLE OF CONTENTS
QUESTIONS...................................................................................................................................3
Question 1....................................................................................................................................3
Question 2....................................................................................................................................4
Question 3....................................................................................................................................5
Question 4....................................................................................................................................6
Question 5....................................................................................................................................7
Question 6....................................................................................................................................8
Question 7....................................................................................................................................9
Question 8..................................................................................................................................10
Question 9..................................................................................................................................11
Question 10................................................................................................................................11
Question 11................................................................................................................................12
REFERENCES..............................................................................................................................14

QUESTIONS
Question 1
(a) Calculation of Figure:
22.2 – 24 / (1.25/ √ 18)
Using simple mathematic principles and square root method where √x= (x)2, the above equation
can be solves as:
= (- 1.8) / (1.25/ 4.24264068711)
= (- 1.8) / (0.29462782549)
= - 6.10940258954
(b) Writing in 2 decimal places:
- 6.11
(c) Calculation of all the following quantities:
(1) 8! / [5! * (8 – 5)!]
Using the BODMAS rule and the integration rule where n! = n * ( n-1) * ( n-2) *…..* 1, the
above calculation can be made as:
= (8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 ) / [ ( 5 * 4 * 3 * 2 * 1) * (3!) ]
= ( 40320 ) / [ ( 120 ) * ( 3 * 2 * 1) ]
= ( 40320 ) / [ ( 120 ) * (6) ]
= ( 40320 ) / [ 720 ]
= 56
(2) 3√ 64
The cube root can be ascertained as 3√x = (x)3. Above calculation can be done as:
= 43
= 64
(3) 73 * 75
Using the exponential rule i.e. an = a * n number of times, the question can be solved as:
= ( 7 * 7 * 7 ) * ( 7 * 7 * 7 * 7 * 7)
= ( 343 ) * ( 16807 )
= 5764801
3

(4) 4-2
Since b-n signifies that 1 / bn , the above question can be resolved as follows:
= 1 / (42)
= 1/ 16
= 0.0625
Question 2
(a) Simplify:
12z – z + 8z
By rearranging, the above equation can be simplified as:
= 12z + 8z - z
= 4z (3 + 2) – z
= 4z * (5) – z
= 20z – z
= 19z
(b) Simplify:
- p – q + 3p
The above equation can be rearranged as:
= -p + 3p – q
= p ( -1 + 3) – q
= p * (2) – q
= 2p – q
(c) Simplify:
2x2 – x – x2
This equation can be simplified as:
= 2x2 – x2 – x
= x2 (2-1) – x
= x2 * (1) – x
= x2 – x
= x (x - 1)
(d) Simplify:
3qp3 – pq3 – q3p + 2p3q
4

The equation above can be rearranged as follows to simplify it:
= 3p3q + 2p3q – pq3 – pq3
= p3q (3 + 2) – pq3 ( 1+ 1)
= p3q ( 5) – pq3 (2)
= 5p3q – 2pq3
= pq ( 5p2 – 2q2)
Question 3
(a) Percentage of reduction
Since the price of the jug was reduced from £9 to £6.30, the percentage decline can be calculated
as:
[(P1 – P0) / P0] * 100
Where,
P1 = New price
P0= Older price
Therefore,
Percentage increase in the price = [( 9 – 6.5) / 6.5 ] * 100
= [ ( 2.5) / 6.5] * 100
= [ 0.38] * 100
= 38%
Therefore, the price of the floral cream jug declined by 38%.
(b) Sale price of the Percy Jones jug whose price declined by 30%
This can be calculated in following manner:
P1 = P0 – (x% decline of P0), where,
P1 is new price
P0 is the old price
X% is the decline.
Therefore,
P1 = 12 – [ 30% of 12]
= 12 – [(30 / 100) * 12]
= 12 – [0.3 * 12]
5

= 12 – 3.6
= £8.4
Therefore, the new price of Percy Jones jug after reduction of 30% is £8.4.
Question 4
(a) Contribution of Saleem in gas bill for January 2018:
It can be ascertained that the Saleem pays 3/ 7 part of the gas bill that is incurred for both Robert
and Saleem. The bill for January was £225 and the amount that Saleem has to contribute can be
ascertained as:
Amount to be contributed = (3 / 7) * 225
= 96.42
= 96 (rounded off)
Therefore the amount that Saleem has to pay as contribution is £96.
(b) Individual Vat calculation for gas bills:
The total vat that is charged in UK on gas bills is 5%of the expense incurred i.e. in the current
case for January 2018, the vat charges are:
£225 * 5%
= 225 * (5 / 100)
= 225 * 0.05
= £11.25
Now amongst the total Vat amount of £11.25, the amount that is to be paid by both Robert and
Saleem can be calculated as:
Saleem: Since Saleem has sharing of 3/7, his contribution in the Vat bill will also be 3/7 i.e.:
= 11.25 * (3 / 7)
= £4.82
Robert: The sharing of Robert will be for the remaining share i.e. for 1 – (3/ 7) which accounts
for the 4/7 share:
= 11.25 * (4/ 7)
= £6.42
Therefore, both Robert and Saleem will have to contribute the above share in the vat of the bill.
6

Question 5
(a) Solve:
3p – 17 = 28
This equation can be solved as:
3p = 28 – 17
3p = 11
P = 11/ 3
P= 3.67
(b) Solve:
3 ( q – 7 ) = 105
This equation can also be solved in following manner:
3q – 21 = 105
3q = 105 – 21
3q = 84
Q = 84 / 3
Q = 28
(c) Solve:
2x – 5 = 5x + 8
To solve this equation, first it can be rearranged in following manner and solution can be
derived:
2x – 5x = 8 + 5
( -3) x = 13
x = 13 / ( -3 )
x = - 4.33
(d) Solve:
45 * 4-2 = 4x
To solve this, first exponentials need to be solved and then value of x can be identified:
As the formula of exponents says that when the base of exponents is same and they are in
multiplication, then the power of such similar bases can be added i.e., ax * ay = a( x + y ). Another
basic one to one property of exponentials is that if, bs = bt, then it implies that s = t for every
7

number or value of b that is unequal to 1 i.e. b ≠ 1. Therefore, in the present equation also similar
properties will be applied in following manner:
4[5 + (-2)] = 4x
4(3) = 4x
Now, as per one to one property,
3 = x
Therefore the value of x = 3.
Question 6
(a) Why the method applied by Osman is correct?
The problem states that Osman while calculating the final payment to be paid for the work
done has included that vat in the final amount calculated by him. The vat was charged as 20% of
the value of any item that is being purchased in UK. The cost of materials that Osman incurred
were £3700 excluding Vat. Now, when Osman was deriving total cost that is to be paid, he
multiplied the amount incurred i.e. £3700 with 1.2. This is a completely right and valid
calculation because Vat here is mark up in the basic cost and 1.2 is a shorter trick of calculating
the total cost. Here, 1.2 is actually 120% that has been written in the decimal format. This 120%
(100% + 20%) includes the 100% i.e. the cost that is incurred and the additional 20% is for the
Vat that is to be paid on £3700.
This is the shorter way of calculating total cost rather than going through the longer method
where first the 20% of the cost i.e. £3700 would have been calculated by multiplying £3700 with
20% and then the amount of Vat thus ascertained would have been added to the original cost of
£3700 so that the total amount that is to be actually paid could be identified.
Therefore, the method that has been adopted by Osman is correct for calculating total
cost is short as well.
(b) Amount of vat that Osman needs to pay:
This can be calculated by directly multiplying the percentage of Vat with the cost incurred:
= £3700 * 20%
= £3700 * ( 20 / 100)
= £3700 * 0.2
= £740
8

If Osman’s method is adopted then, first the total cost will be derived by multiplication of £3700
with 1.2 and then the original cost will be subtracted from the new cost thus helping in
calculation of the vat amount:
New cost or Total Cost = £3700 * 1.2
= £4440
Now, the older cost will be deducted from new cost i.e.:
Vat amount = £4440 - £3700
= £740
Question 7
Equation solving through elimination method
Both the equations can be marked as equation 1 and equation 2:
3y = - 2x + 6 ---------(1)
Y = 2x – 2 ------------(2)
Now adding the second equation with the first will help in the elimination of x variable:
3y = - 2x + 6
(+) Y = (+) 2x – (+) 2
4y = 0 + 4 ------------- (the positive 2x and the negative 2x got cancelled thus resulting in 0)
4y = 4
Y = 4/ 4
Y = 1
Now the value of y thus obtained can be substituted in the equation 2 so that value of x can be
ascertained:
Y = 2x – 2,
1 = 2x – 2
1 + 2 = 2x
3 = 2x
3/ 2 = x
1.5 = x
Therefore the value of x = 1.5 and the value of y = 1.
Now these values can be put in the equation to solve them:
9

Equation 1:
3y = - 2x + 6,
3 (1) = -2 (1.5) + 6
3 = -3 + 6
3 = 3
Equation 2:
Y = 2x – 2,
(1) = 2 (1.5) - 2
1 = 3 – 2
1 = 1
Question 8
(a) Weight of the leg of lamb
It has been said that the price of the leg of lamb that weighs 1.5 kg is £5.22 and the price for 2.4
kg needs to be ascertained. This can be done in following manner through the unitary problem
solving method:
Since, price of 1.5 kg of leg of lamb = £5.22
Therefore, price of 1 kg of leg of lamb = £5.22 / 1.5 kg
Hence, price of 2.4 kg of leg of lamb = (£5.22 / 1.5 kg) * 2.4 kg
Therefore, the price of 2.4 kg leg is = 3.48 * 2.4
= 8.352
Hence, for 2.4 kg of leg of lamb, the price that will be charged is £8.35.
(b) Number of men required to complete the task
In order to paint a house in 10.5 days, the number of men required by a decorator is 4. So in
order to identify the number of men required to paint the house in only 7 days, the number of
men that would be required can be calculated in following manner:
Since, number of men required to paint house in 10.5 days = 4 men
Therefore, work done by these men = 10.5 days * 4
Since, similar work needs to be done, work done by x men in 7 days will be equivalent.
Therefore, total number of x men required to paint the house, following equation can be
developed:
10

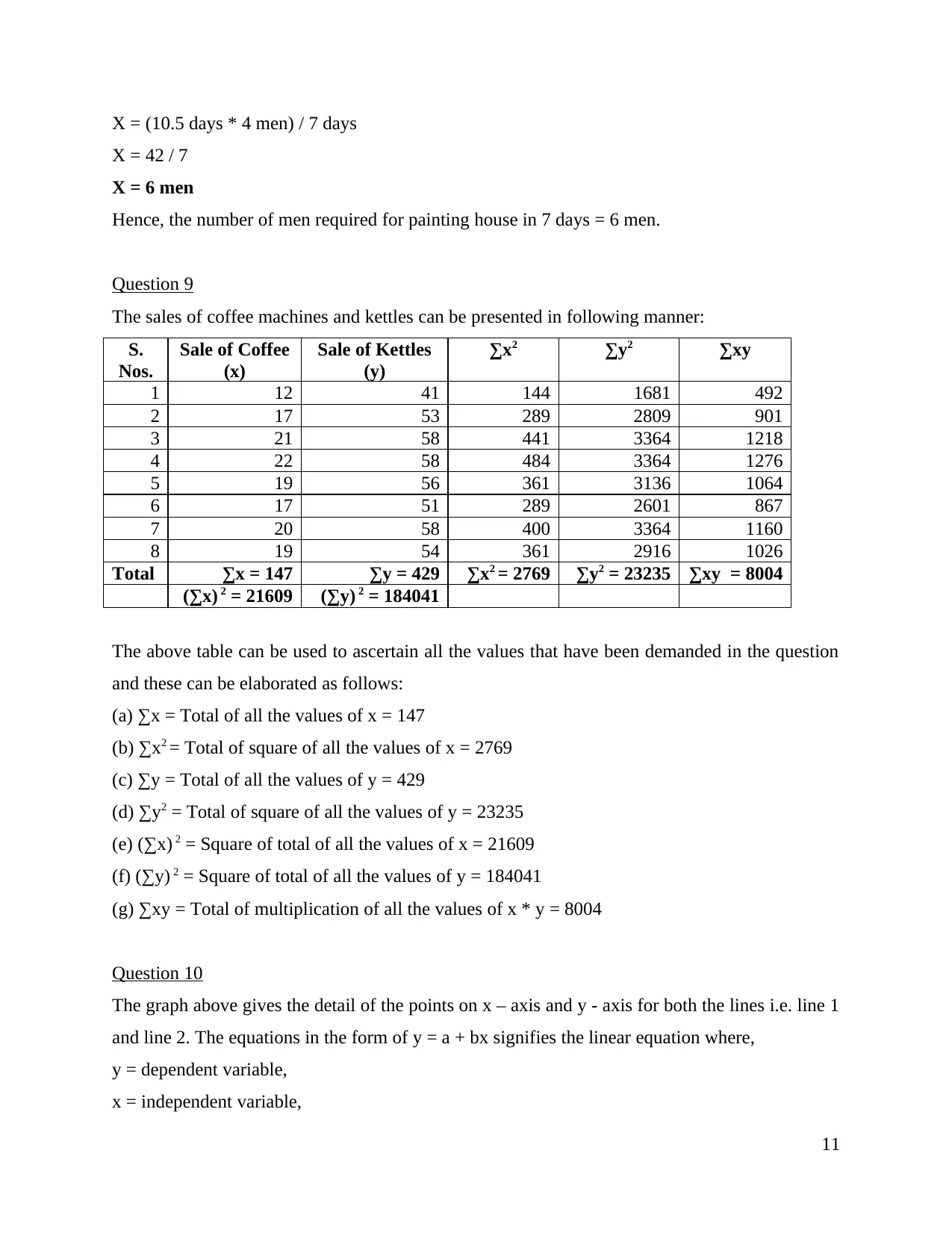
X = (10.5 days * 4 men) / 7 days
X = 42 / 7
X = 6 men
Hence, the number of men required for painting house in 7 days = 6 men.
Question 9
The sales of coffee machines and kettles can be presented in following manner:
S.
Nos.
Sale of Coffee
(x)
Sale of Kettles
(y)
∑x2 ∑y2 ∑xy
1 12 41 144 1681 492
2 17 53 289 2809 901
3 21 58 441 3364 1218
4 22 58 484 3364 1276
5 19 56 361 3136 1064
6 17 51 289 2601 867
7 20 58 400 3364 1160
8 19 54 361 2916 1026
Total ∑x = 147 ∑y = 429 ∑x2 = 2769 ∑y2 = 23235 ∑xy = 8004
(∑x) 2 = 21609 (∑y) 2 = 184041
The above table can be used to ascertain all the values that have been demanded in the question
and these can be elaborated as follows:
(a) ∑x = Total of all the values of x = 147
(b) ∑x2 = Total of square of all the values of x = 2769
(c) ∑y = Total of all the values of y = 429
(d) ∑y2 = Total of square of all the values of y = 23235
(e) (∑x) 2 = Square of total of all the values of x = 21609
(f) (∑y) 2 = Square of total of all the values of y = 184041
(g) ∑xy = Total of multiplication of all the values of x * y = 8004
Question 10
The graph above gives the detail of the points on x – axis and y - axis for both the lines i.e. line 1
and line 2. The equations in the form of y = a + bx signifies the linear equation where,
y = dependent variable,
x = independent variable,
11

a = y intercept i.e. y coordinate ( 0, a) and
b = slope i.e. (Ay – By / (Ax - Bx).
Here, Ax = x coordinate of point A
Bx = x coordinate of point B
Ay = y coordinate of point A
By = y coordinate of point B
a and b are constant numbers that are derived from the graph lines.
In the present scenario, for line 1, the A coordinates are (0, 5) and B coordinates are (2.5, 0) the
equation can be developed as:
a = (0 ,5)
b = (5 - 0) / ( 0 – 2.5)
= - 2.5
Hence,
y = 5 - 2.5x
The equation for line 2 where there is only A coordinate i.e. (0, 2) and B coordinate is (0, 0) is:
a = (0, 2)
b = (2 - 0) / (0 - 0)
= 0
Hence,
y = 2 + 0x or y = 2
Question 11
In the above case, it can be clearly ascertained that the Linear programming needs to be
developed where the profit maximisation is the key objective. There are two alternatives i.e.
combination boilers and the traditional boilers and the constraints is in the form of limited
number of hours available for gas flow test and electrical test.
(a) Expression for monthly profits
This can be done by following a series of steps i.e.:
Step 1: Assume that Combination boilers is x1 and traditional boilers is x2. The profit every
month for x1 is £250 and for x2 it is £130. Now the equation for profit maximization can be
developed as:
z = 250 x1 + 130 x2 where z is the profit that needs to be maximised.
12

(b) Inequalities representing constraints
The constraints as it was identified were,
Gas flow hours that can be maximum at 160 hours per month
Electricity test hours that can be 210 hours maximum per month
Based on the following table, inequality formulation can be made easier:
Combination boilers
(x1)
Traditional boilers
(x2)
Constraints Equation
Profit (z) 250 130 z = 250 x1 + 130 x2
Gas flow
Test hours
30 minutes 40 minutes 160 hours i.e.
9600 minutes
30x 1+ 40x2 ≤ 9600
Electricity
test hours
20 minutes 30 minutes 210 hours i.e.
12600 minutes
20x 1+ 30x2 ≤ 12600
The inequality equations thus developed are:
30x 1+ 40x2 ≤ 9600
20x 1+ 30x2 ≤ 12600
Therefore, collectively, the entire linear programming equation can be developed as:
Maximise,
Z = 250 x1 + 130 x2
Subjected to,
30x 1+ 40x2 ≤ 9600
20x 1+ 30x2 ≤ 12600
13

REFERENCES
Books and Journals
Online
14