Mathematics Major: RSA Cryptography and Prime Number Analysis

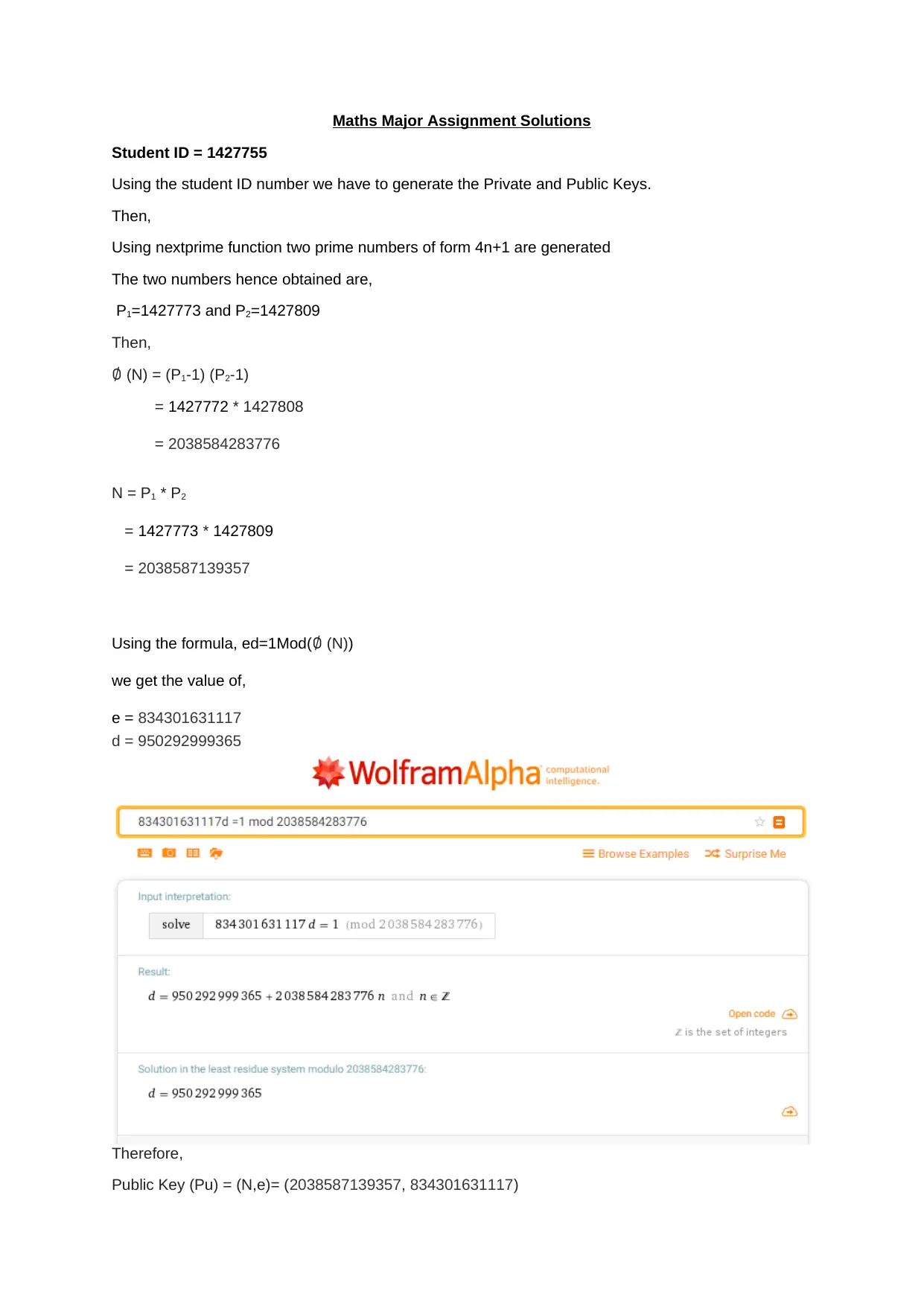
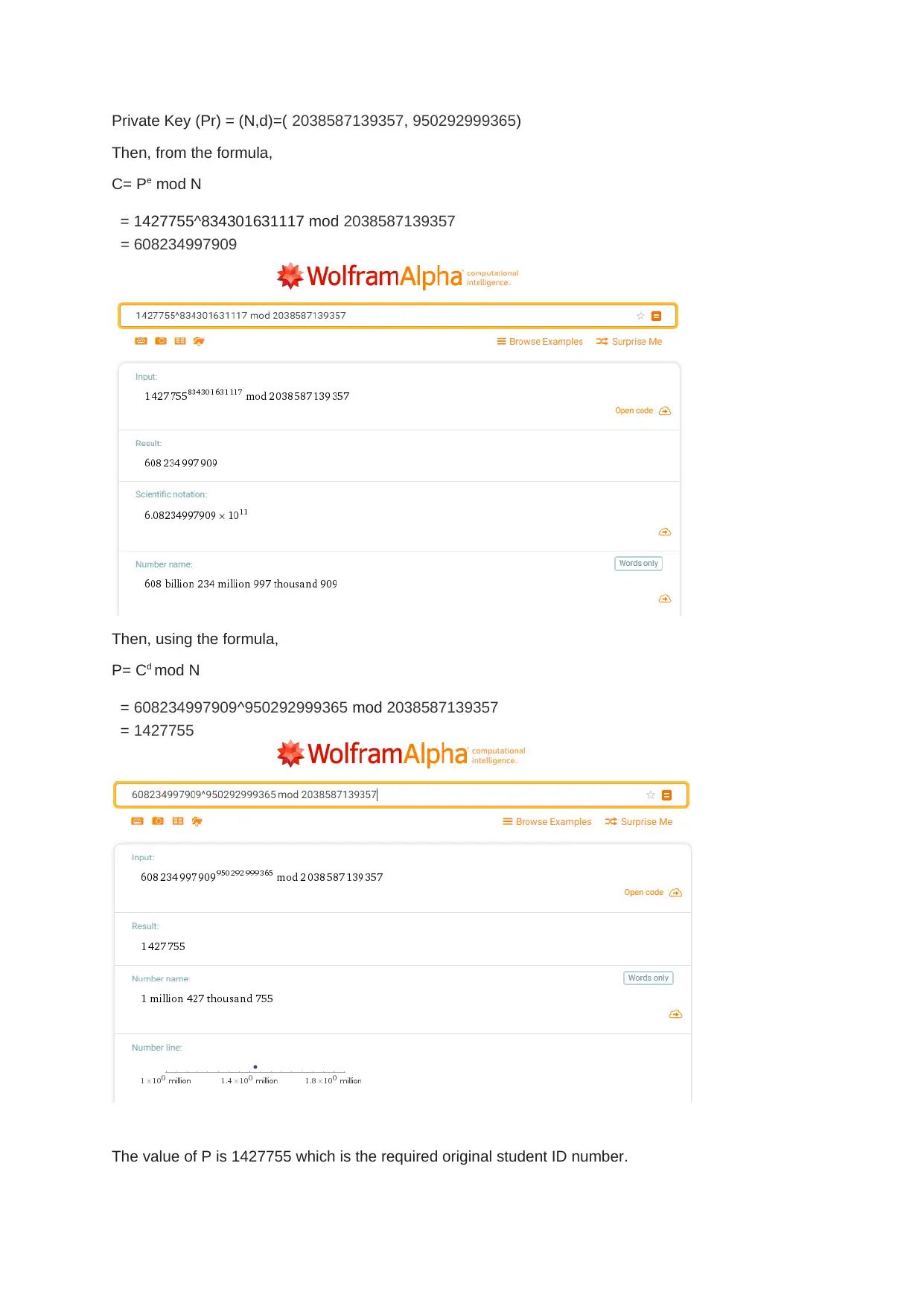
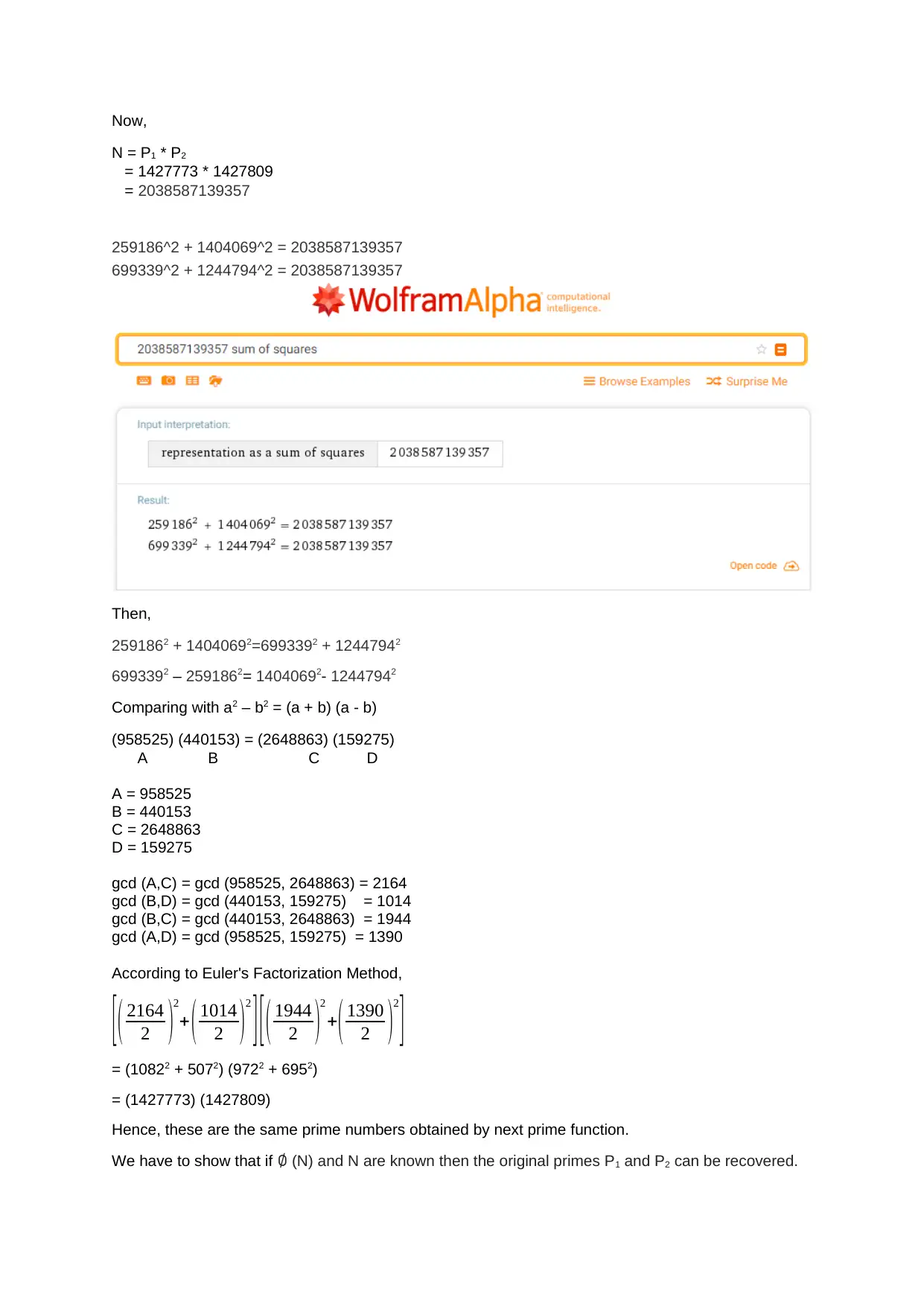
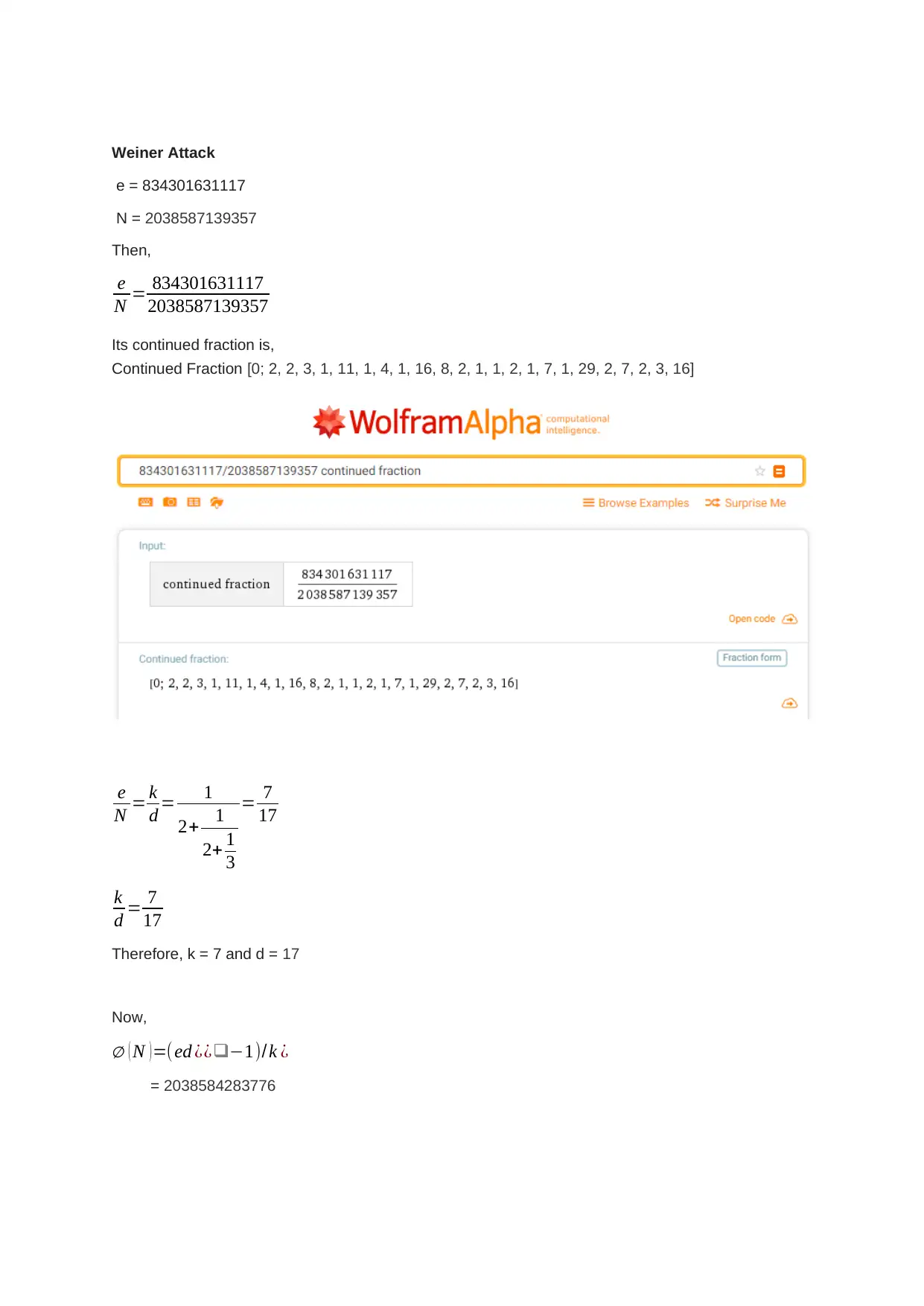
This assignment delves into the core concepts of RSA cryptography. It begins by generating public and private keys using a student ID and the nextprime function to find two prime numbers of the form 4n+1. The solution then demonstrates the encryption and decryption processes using modular e...Read More

Maths Major Assignment Solutions
Student ID = 1427755
Using the student ID number we have to generate the Private and Public Keys.
Then,
Using nextprime function two prime numbers of form 4n+1 are generated
The two numbers hence obtained are,
P1=1427773 and P2=1427809
Then,
∅ (N) = (P1-1) (P2-1)
= 1427772 * 1427808
= 2038584283776
N = P1 * P2
= 1427773 * 1427809
= 2038587139357
Using the formula, ed=1Mod(∅ (N))
we get the value of,
e = 834301631117
d = 950292999365
Therefore,
Public Key (Pu) = (N,e)= (2038587139357, 834301631117)

Private Key (Pr) = (N,d)=( 2038587139357, 950292999365)
Then, from the formula,
C= Pe mod N
= 1427755^834301631117 mod 2038587139357
= 608234997909
Then, using the formula,
P= Cd mod N
= 608234997909^950292999365 mod 2038587139357
= 1427755
The value of P is 1427755 which is the required original student ID number.

Breaking the keys:
P1= 1427773
P2= 1427809
The numbers P1 and P2 are then represented as the sum of two squares.
(1082)2 + (507)2 = 1427773
(695)2 + (972)2 = 1427809
Then, two right angled triangles are drawn,
So, For the 1st triangle
C = n2 + (2m + n - 1)2
= 5072 + (2m + 507 - 1)2
(1082)2 = (2m + 507 - 1)2
2m = 1082–506
m = 288
So, (m1, n1) = (288, 507)
For 2nd triangle,
C = n2 + (2m + n - 1)2
= 6952 + (2m + 695 - 1)2
(972)2 = (2m + 695 - 1)2
2m = 972 – 694
m = 139
So, (m2, n2) = (139, 695)
√1427773
507
1082
√1427809
695
972

Now, Let P1 = C1 and P2 = C2 and let the smallest value of the two squares be n
For the 1st triangle,
a = (2m - 1)(2m + 2n - 1)
= (576 -1) (576 + 1014 - 1)
= 913675
b = 2n (n + 2n -1)
= 1014 (507+ 1014 -1)
= 1541280
C = n2 + (2m + n - 1)2
= 257049 + (576 + 507 - 1)2
= 1427773
For the 2nd triangle,
a = (2m - 1)(2m + 2n - 1)
= (278 - 1)(278 +1390 -1)
= 461759
b = 2n (n + 2n -1)
= 1390 (695 + 1390 -1)
= 2896760
C = n2 + (2m + n - 1)2
= 483025 + (278+695-1)2
=483025 +944784
= 1427809
c1
a1
b1
c2
a2
b2

Now,
N = P1 * P2
= 1427773 * 1427809
= 2038587139357
259186^2 + 1404069^2 = 2038587139357
699339^2 + 1244794^2 = 2038587139357
Then,
2591862 + 14040692=6993392 + 12447942
6993392 – 2591862= 14040692- 12447942
Comparing with a2 – b2 = (a + b) (a - b)
(958525) (440153) = (2648863) (159275)
A B C D
A = 958525
B = 440153
C = 2648863
D = 159275
gcd (A,C) = gcd (958525, 2648863) = 2164
gcd (B,D) = gcd (440153, 159275) = 1014
gcd (B,C) = gcd (440153, 2648863) = 1944
gcd (A,D) = gcd (958525, 159275) = 1390
According to Euler's Factorization Method,
[ ( 2164
2 )
2
+ ( 1014
2 )
2
][ ( 1944
2 )
2
+( 1390
2 )
2
]
= (10822 + 5072) (9722 + 6952)
= (1427773) (1427809)
Hence, these are the same prime numbers obtained by next prime function.
We have to show that if ∅ (N) and N are known then the original primes P1 and P2 can be recovered.

N = P1 * P2
= 1427773* 1427809
= 2038587139357
∅ (N) = (P1-1) (P2-1)
= (1427773- 1) (1427809 - 1)
= 2038584283776
We have,
∅ (N) = (P1-1) (P2-1)
∅ (N) = P1P2 – P1 – P2 + 1
∅ (N) = N – P1 – P2 + 1
P1 + P2 = N - ∅ (N) +1
Then,
P2 = N - ∅ (N) +1 – P1
P1 = N - ∅ (N) +1 – P2
So,
N = P1 (N - ∅ (N) +1 – P1)
= P1N – P1∅ (N) + P1- P12
0 = P12 + P1 (∅ (N) – N - 1) + N
Comparing with the equation ax2 + bx + c = 0, x=−b ± √ b2−4 ac
2 a
a = 1
b = ∅ (N) – N – 1
= -2855582
c = 2038587139357
Then, putting the values of a, b and c in the equation,
For negative sign, x = 1427773 = P1
For positive sign, x = 1427809 = P2

Weiner Attack
e = 834301631117
N = 2038587139357
Then,
e
N = 834301631117
2038587139357
Its continued fraction is,
Continued Fraction [0; 2, 2, 3, 1, 11, 1, 4, 1, 16, 8, 2, 1, 1, 2, 1, 7, 1, 29, 2, 7, 2, 3, 16]
e
N = k
d = 1
2+ 1
2+ 1
3
= 7
17
k
d = 7
17
Therefore, k = 7 and d = 17
Now,
∅ ( N ) =(ed ¿¿❑−1)/k ¿
= 2038584283776

We have,
∅ (N) = (P1-1) (P2-1)
∅ (N) = P1P2 – P1 – P2 + 1
∅ (N) = N – P1 – P2 + 1
P1 + P2 = N - ∅ (N) +1
Then,
P2 = N - ∅ (N) +1 – P1
P1 = N - ∅ (N) +1 – P2
So,
N = P1 (N - ∅ (N) +1 – P1)
= P1N – P1∅ (N) + P1- P12
0 = P12 + P1 (∅ (N) – N - 1) + N
Comparing with the equation ax2 + bx + c = 0, x=−b ± √ b2−4 ac
2 a
a = 1
b = ∅ (N) – N – 1
= -2855582
c = 2038587139357
Then, putting the values of a, b and c in the equation,
For negative sign, x = 1427773 = P1
For positive sign, x = 1427809 = P2