Statistics and Probability Assignment: Comprehensive Problem Solving
VerifiedAdded on 2020/06/05
|10
|1763
|41
Homework Assignment
AI Summary
This document presents a comprehensive solution to a statistics and probability assignment. The assignment covers various topics, including calculating the mean and standard deviation from grouped data, determining cumulative frequencies, finding quartiles and the interquartile range, and constru...

Maths - Statistics and
Probability
Probability
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
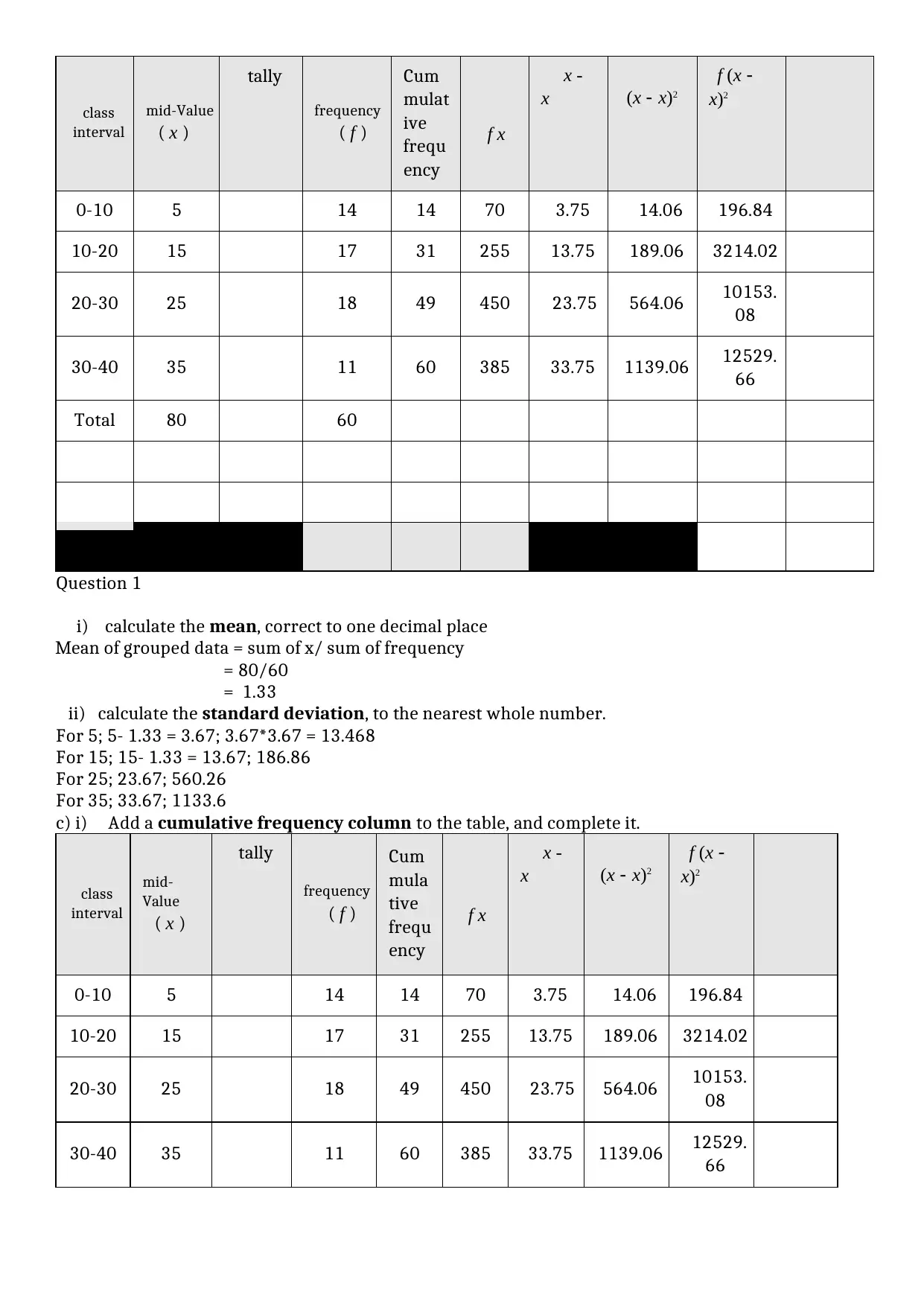
class
interval
mid-Value
( x )
tally
frequency
( f )
Cum
mulat
ive
frequ
ency
f x
x -
x (x - x)2
f (x -
x)2
0-10 5 14 14 70 3.75 14.06 196.84
10-20 15 17 31 255 13.75 189.06 3214.02
20-30 25 18 49 450 23.75 564.06 10153.
08
30-40 35 11 60 385 33.75 1139.06 12529.
66
Total 80 60
Question 1
i) calculate the mean, correct to one decimal place
Mean of grouped data = sum of x/ sum of frequency
= 80/60
= 1.33
ii) calculate the standard deviation, to the nearest whole number.
For 5; 5- 1.33 = 3.67; 3.67*3.67 = 13.468
For 15; 15- 1.33 = 13.67; 186.86
For 25; 23.67; 560.26
For 35; 33.67; 1133.6
c) i) Add a cumulative frequency column to the table, and complete it.
class
interval
mid-
Value
( x )
tally
frequency
( f )
Cum
mula
tive
frequ
ency
f x
x -
x (x - x)2
f (x -
x)2
0-10 5 14 14 70 3.75 14.06 196.84
10-20 15 17 31 255 13.75 189.06 3214.02
20-30 25 18 49 450 23.75 564.06 10153.
08
30-40 35 11 60 385 33.75 1139.06 12529.
66
interval
mid-Value
( x )
tally
frequency
( f )
Cum
mulat
ive
frequ
ency
f x
x -
x (x - x)2
f (x -
x)2
0-10 5 14 14 70 3.75 14.06 196.84
10-20 15 17 31 255 13.75 189.06 3214.02
20-30 25 18 49 450 23.75 564.06 10153.
08
30-40 35 11 60 385 33.75 1139.06 12529.
66
Total 80 60
Question 1
i) calculate the mean, correct to one decimal place
Mean of grouped data = sum of x/ sum of frequency
= 80/60
= 1.33
ii) calculate the standard deviation, to the nearest whole number.
For 5; 5- 1.33 = 3.67; 3.67*3.67 = 13.468
For 15; 15- 1.33 = 13.67; 186.86
For 25; 23.67; 560.26
For 35; 33.67; 1133.6
c) i) Add a cumulative frequency column to the table, and complete it.
class
interval
mid-
Value
( x )
tally
frequency
( f )
Cum
mula
tive
frequ
ency
f x
x -
x (x - x)2
f (x -
x)2
0-10 5 14 14 70 3.75 14.06 196.84
10-20 15 17 31 255 13.75 189.06 3214.02
20-30 25 18 49 450 23.75 564.06 10153.
08
30-40 35 11 60 385 33.75 1139.06 12529.
66

Total 80 60
ii) Use this column to help you find approximations for the 1st and 3rd quartiles, and thus…
For calculating the 1st and 3rd quartiles, we have to follow the steps below:
1st QR = (n + 1) / 4
= ( 40 + 1) /4
= 10.25
2nd QR = (n + 1) / 4 *2
= 10.25 * 2
= 20.5
We also have to find the 3rd QR for calculating the interquartile range,
3rd QR = (n + 1) / 4 *3
= 10.25 *3
= 30.75
iii) calculate the interquartile range.
IQR = Q3 - Q1
= 30.75-10.25
= 20.5
d) i) Construct a cumulative frequency polygon (you may choose to overlay it with an ogive).
ii) Use this column to help you find approximations for the 1st and 3rd quartiles, and thus…
For calculating the 1st and 3rd quartiles, we have to follow the steps below:
1st QR = (n + 1) / 4
= ( 40 + 1) /4
= 10.25
2nd QR = (n + 1) / 4 *2
= 10.25 * 2
= 20.5
We also have to find the 3rd QR for calculating the interquartile range,
3rd QR = (n + 1) / 4 *3
= 10.25 *3
= 30.75
iii) calculate the interquartile range.
IQR = Q3 - Q1
= 30.75-10.25
= 20.5
d) i) Construct a cumulative frequency polygon (you may choose to overlay it with an ogive).
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
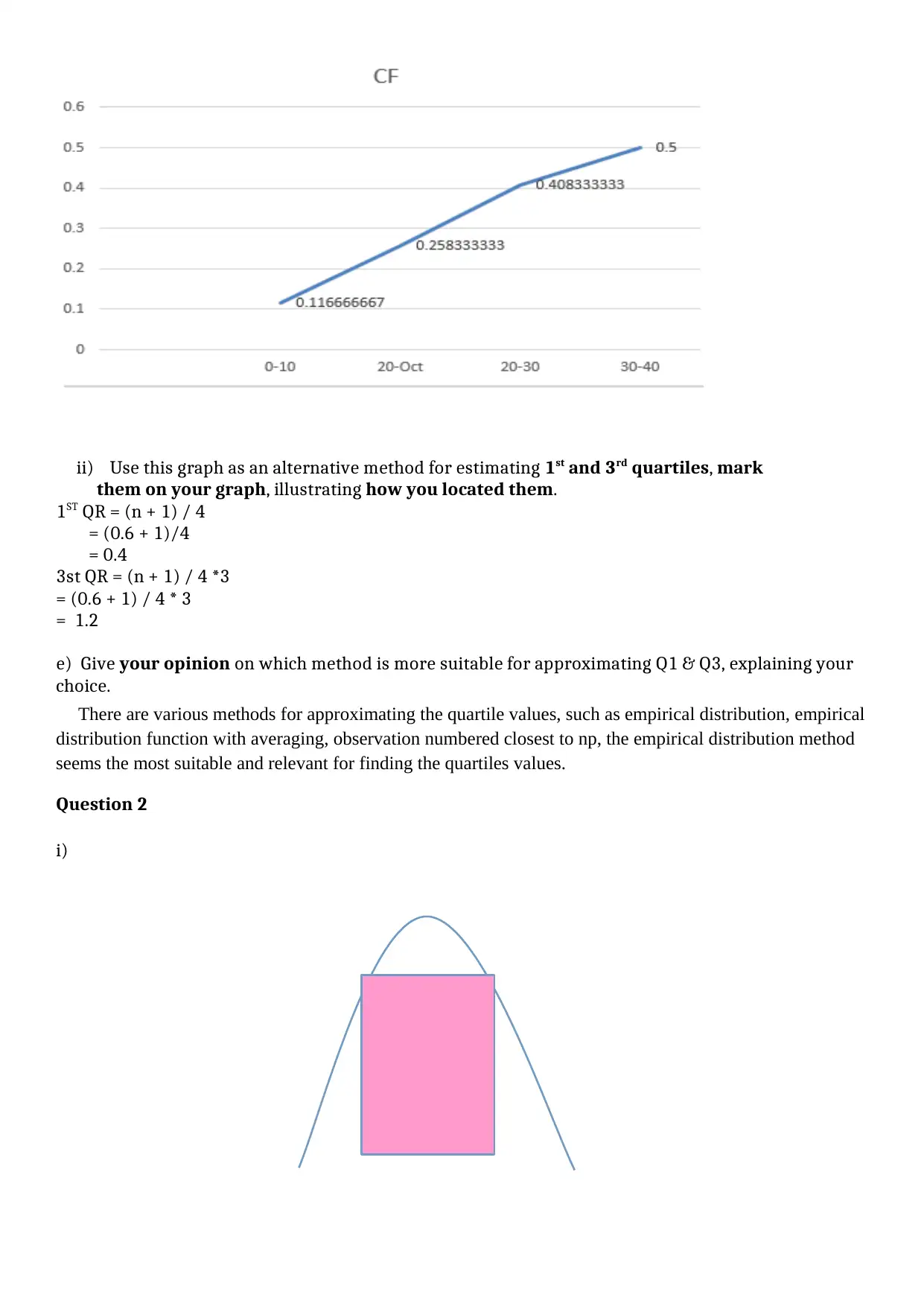
ii) Use this graph as an alternative method for estimating 1st and 3rd quartiles, mark
them on your graph, illustrating how you located them.
1ST QR = (n + 1) / 4
= (0.6 + 1)/4
= 0.4
3st QR = (n + 1) / 4 *3
= (0.6 + 1) / 4 * 3
= 1.2
e) Give your opinion on which method is more suitable for approximating Q1 & Q3, explaining your
choice.
There are various methods for approximating the quartile values, such as empirical distribution, empirical
distribution function with averaging, observation numbered closest to np, the empirical distribution method
seems the most suitable and relevant for finding the quartiles values.
Question 2
i)
them on your graph, illustrating how you located them.
1ST QR = (n + 1) / 4
= (0.6 + 1)/4
= 0.4
3st QR = (n + 1) / 4 *3
= (0.6 + 1) / 4 * 3
= 1.2
e) Give your opinion on which method is more suitable for approximating Q1 & Q3, explaining your
choice.
There are various methods for approximating the quartile values, such as empirical distribution, empirical
distribution function with averaging, observation numbered closest to np, the empirical distribution method
seems the most suitable and relevant for finding the quartiles values.
Question 2
i)
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

· Secondly, calculate the proportions or probabilities.
a) p(-0.32 < z < 2.11)
After analyzing the table for cumulative properties of the standard normal distribution, we got the
values of P(Z<2.11) AND P(Z<-0.32)
p(-0.32 < z < 2.11)
= P(Z<2.11) - P(Z<-0.32)
= 0.98257 - 0.37448
= 0.60809
b) For the same 30 athletes in b), estimate the number of athletes you would expect to have a
vertical leap greater than 107cm.
The estimation is represented in terms of the following graph :
Question 3
a) (i) Give definitions for the mean and median to distinguish between them.
Mean : The mean is considered as a mathematical function consisting a range of values or quantities.
Median : Median is considered as a way of determining the average of a group of numbers.
(ii) Median can be considered as a better method for the measurement of the central tendency as it
seems quite easy and simple to compute it and is not distorted by the skewed data.
a) p(-0.32 < z < 2.11)
After analyzing the table for cumulative properties of the standard normal distribution, we got the
values of P(Z<2.11) AND P(Z<-0.32)
p(-0.32 < z < 2.11)
= P(Z<2.11) - P(Z<-0.32)
= 0.98257 - 0.37448
= 0.60809
b) For the same 30 athletes in b), estimate the number of athletes you would expect to have a
vertical leap greater than 107cm.
The estimation is represented in terms of the following graph :
Question 3
a) (i) Give definitions for the mean and median to distinguish between them.
Mean : The mean is considered as a mathematical function consisting a range of values or quantities.
Median : Median is considered as a way of determining the average of a group of numbers.
(ii) Median can be considered as a better method for the measurement of the central tendency as it
seems quite easy and simple to compute it and is not distorted by the skewed data.
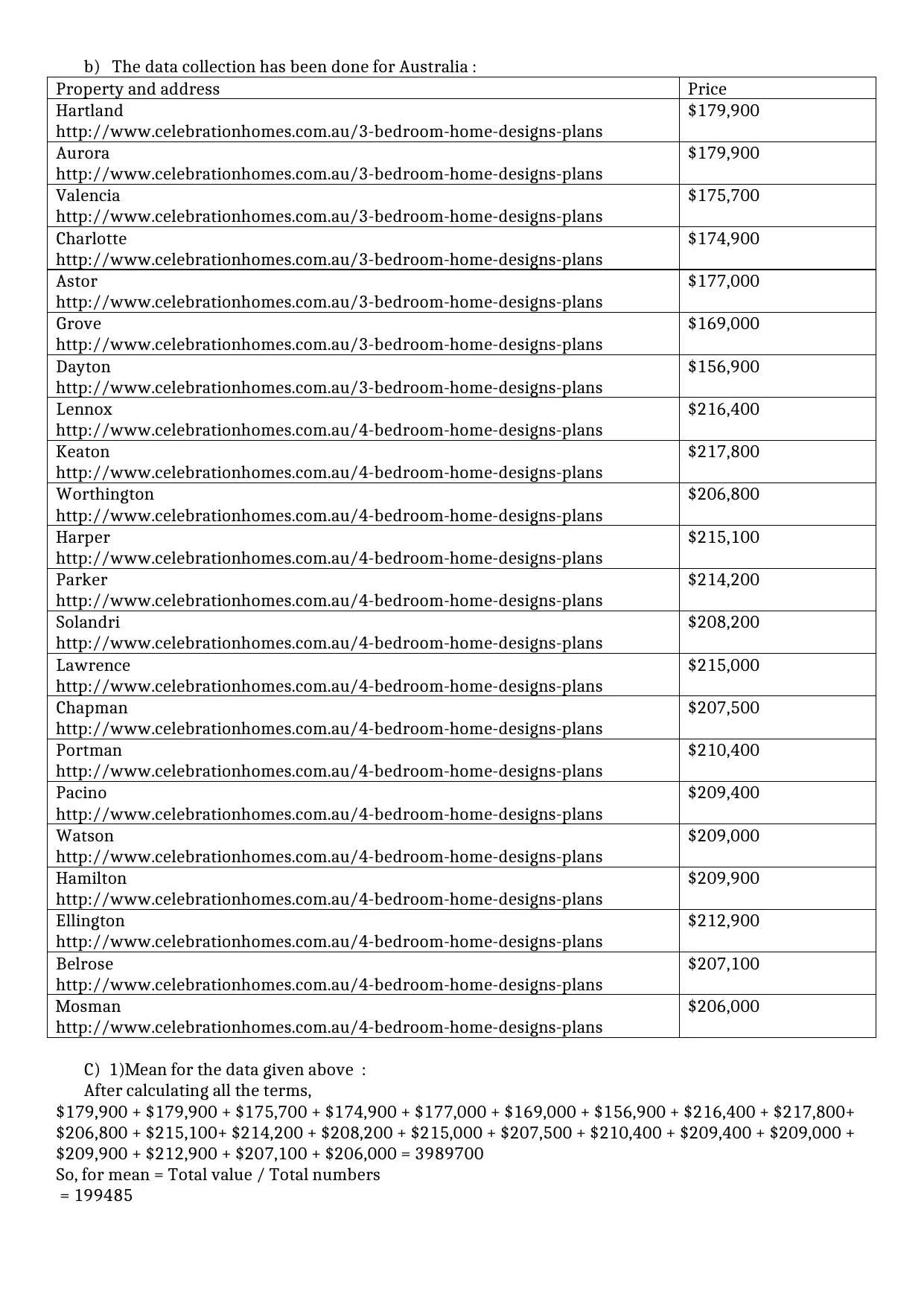
b) The data collection has been done for Australia :
Property and address Price
Hartland
http://www.celebrationhomes.com.au/3-bedroom-home-designs-plans
$179,900
Aurora
http://www.celebrationhomes.com.au/3-bedroom-home-designs-plans
$179,900
Valencia
http://www.celebrationhomes.com.au/3-bedroom-home-designs-plans
$175,700
Charlotte
http://www.celebrationhomes.com.au/3-bedroom-home-designs-plans
$174,900
Astor
http://www.celebrationhomes.com.au/3-bedroom-home-designs-plans
$177,000
Grove
http://www.celebrationhomes.com.au/3-bedroom-home-designs-plans
$169,000
Dayton
http://www.celebrationhomes.com.au/3-bedroom-home-designs-plans
$156,900
Lennox
http://www.celebrationhomes.com.au/4-bedroom-home-designs-plans
$216,400
Keaton
http://www.celebrationhomes.com.au/4-bedroom-home-designs-plans
$217,800
Worthington
http://www.celebrationhomes.com.au/4-bedroom-home-designs-plans
$206,800
Harper
http://www.celebrationhomes.com.au/4-bedroom-home-designs-plans
$215,100
Parker
http://www.celebrationhomes.com.au/4-bedroom-home-designs-plans
$214,200
Solandri
http://www.celebrationhomes.com.au/4-bedroom-home-designs-plans
$208,200
Lawrence
http://www.celebrationhomes.com.au/4-bedroom-home-designs-plans
$215,000
Chapman
http://www.celebrationhomes.com.au/4-bedroom-home-designs-plans
$207,500
Portman
http://www.celebrationhomes.com.au/4-bedroom-home-designs-plans
$210,400
Pacino
http://www.celebrationhomes.com.au/4-bedroom-home-designs-plans
$209,400
Watson
http://www.celebrationhomes.com.au/4-bedroom-home-designs-plans
$209,000
Hamilton
http://www.celebrationhomes.com.au/4-bedroom-home-designs-plans
$209,900
Ellington
http://www.celebrationhomes.com.au/4-bedroom-home-designs-plans
$212,900
Belrose
http://www.celebrationhomes.com.au/4-bedroom-home-designs-plans
$207,100
Mosman
http://www.celebrationhomes.com.au/4-bedroom-home-designs-plans
$206,000
C) 1)Mean for the data given above :
After calculating all the terms,
$179,900 + $179,900 + $175,700 + $174,900 + $177,000 + $169,000 + $156,900 + $216,400 + $217,800+
$206,800 + $215,100+ $214,200 + $208,200 + $215,000 + $207,500 + $210,400 + $209,400 + $209,000 +
$209,900 + $212,900 + $207,100 + $206,000 = 3989700
So, for mean = Total value / Total numbers
= 199485
Property and address Price
Hartland
http://www.celebrationhomes.com.au/3-bedroom-home-designs-plans
$179,900
Aurora
http://www.celebrationhomes.com.au/3-bedroom-home-designs-plans
$179,900
Valencia
http://www.celebrationhomes.com.au/3-bedroom-home-designs-plans
$175,700
Charlotte
http://www.celebrationhomes.com.au/3-bedroom-home-designs-plans
$174,900
Astor
http://www.celebrationhomes.com.au/3-bedroom-home-designs-plans
$177,000
Grove
http://www.celebrationhomes.com.au/3-bedroom-home-designs-plans
$169,000
Dayton
http://www.celebrationhomes.com.au/3-bedroom-home-designs-plans
$156,900
Lennox
http://www.celebrationhomes.com.au/4-bedroom-home-designs-plans
$216,400
Keaton
http://www.celebrationhomes.com.au/4-bedroom-home-designs-plans
$217,800
Worthington
http://www.celebrationhomes.com.au/4-bedroom-home-designs-plans
$206,800
Harper
http://www.celebrationhomes.com.au/4-bedroom-home-designs-plans
$215,100
Parker
http://www.celebrationhomes.com.au/4-bedroom-home-designs-plans
$214,200
Solandri
http://www.celebrationhomes.com.au/4-bedroom-home-designs-plans
$208,200
Lawrence
http://www.celebrationhomes.com.au/4-bedroom-home-designs-plans
$215,000
Chapman
http://www.celebrationhomes.com.au/4-bedroom-home-designs-plans
$207,500
Portman
http://www.celebrationhomes.com.au/4-bedroom-home-designs-plans
$210,400
Pacino
http://www.celebrationhomes.com.au/4-bedroom-home-designs-plans
$209,400
Watson
http://www.celebrationhomes.com.au/4-bedroom-home-designs-plans
$209,000
Hamilton
http://www.celebrationhomes.com.au/4-bedroom-home-designs-plans
$209,900
Ellington
http://www.celebrationhomes.com.au/4-bedroom-home-designs-plans
$212,900
Belrose
http://www.celebrationhomes.com.au/4-bedroom-home-designs-plans
$207,100
Mosman
http://www.celebrationhomes.com.au/4-bedroom-home-designs-plans
$206,000
C) 1)Mean for the data given above :
After calculating all the terms,
$179,900 + $179,900 + $175,700 + $174,900 + $177,000 + $169,000 + $156,900 + $216,400 + $217,800+
$206,800 + $215,100+ $214,200 + $208,200 + $215,000 + $207,500 + $210,400 + $209,400 + $209,000 +
$209,900 + $212,900 + $207,100 + $206,000 = 3989700
So, for mean = Total value / Total numbers
= 199485
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Standard deviation =
2) Calculate the 95% confidence interval for the mean population using your sample statistics
calculations in (c).
D) There is a wide range of flats for the three bedroom sets and each one on a ma are below the value
of $400,00.
Question 3 (continued over)
Null hypothesis : When there are no significant differences between the specified populations, it is
considered as the null hypothesis.
Alternate hypothesis : It is often denoted by H1 or Ha and some observations have been influenced
by causes of a non random possibility.
There are two types of one tailed tests which includes the right tailed and the left tailed. The point
where rejection of the null hypothesis has been done is referred as in the one tail.
Question 3
c) Describe how your sample mean compares with the critical value (upper or lower limit of
acceptance region).
The sample mean is considered as a set of features from a distribution defined by. It is referred
as the unbiased estimator for the mean population. A critical value is categorized as a point on a test
scale after which the null hypothesis can be rejected.
d) Thus, state which hypothesis is supported, and which should be rejected, and create a written
conclusion to summarize your investigation.
2) Calculate the 95% confidence interval for the mean population using your sample statistics
calculations in (c).
D) There is a wide range of flats for the three bedroom sets and each one on a ma are below the value
of $400,00.
Question 3 (continued over)
Null hypothesis : When there are no significant differences between the specified populations, it is
considered as the null hypothesis.
Alternate hypothesis : It is often denoted by H1 or Ha and some observations have been influenced
by causes of a non random possibility.
There are two types of one tailed tests which includes the right tailed and the left tailed. The point
where rejection of the null hypothesis has been done is referred as in the one tail.
Question 3
c) Describe how your sample mean compares with the critical value (upper or lower limit of
acceptance region).
The sample mean is considered as a set of features from a distribution defined by. It is referred
as the unbiased estimator for the mean population. A critical value is categorized as a point on a test
scale after which the null hypothesis can be rejected.
d) Thus, state which hypothesis is supported, and which should be rejected, and create a written
conclusion to summarize your investigation.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Alternate hypothesis could be supported and null hypothesis should be rejected. The reason behind is
that in a null hypothesis, no statistical significance is present within the two factors.
e) (i)
The examples of a good statistical sample includes the following :
Box and whisker plots
Evaluation of data and making of the conjectures
(ii)
We could have improved our sampling method by including the probability sampling of type multi
phase sample. It takes any form of random selection. For that it is necessary to set up some
procedures or processes ensuring the parts in the specific population having similar number of
probabilities.
Question 4: ‘A Bit Dicey’
Dice Total $1 to play game refunded Additional $2 prize
Double AND (Total 8 or less) Yes No
Total more than 8 Yes Yes
Double AND (Total more than 8) No Yes
Everything else No No
a)
Probability is considered as the suitable and relevant method.
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
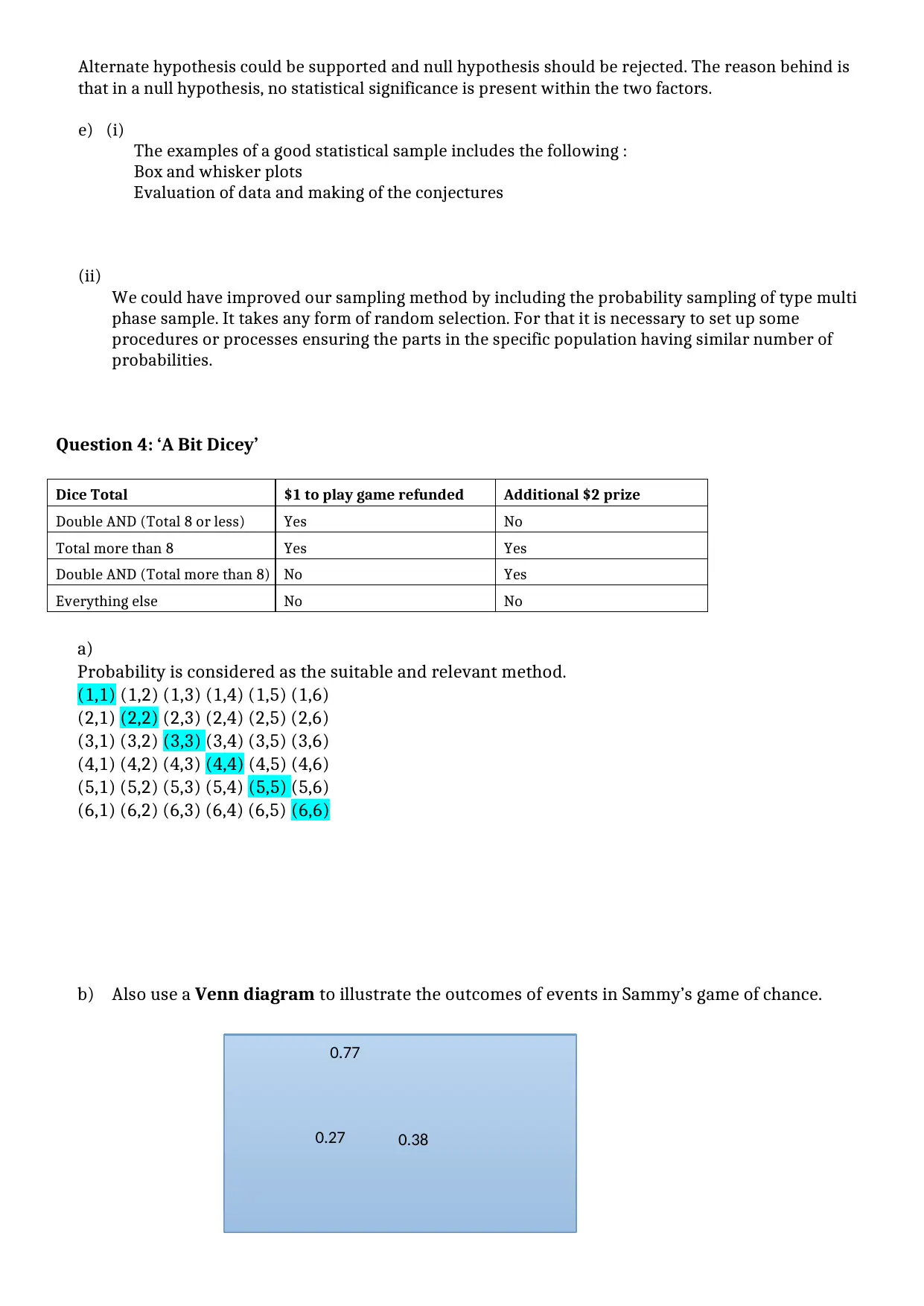
b) Also use a Venn diagram to illustrate the outcomes of events in Sammy’s game of chance.
0.27 0.38
0.77
that in a null hypothesis, no statistical significance is present within the two factors.
e) (i)
The examples of a good statistical sample includes the following :
Box and whisker plots
Evaluation of data and making of the conjectures
(ii)
We could have improved our sampling method by including the probability sampling of type multi
phase sample. It takes any form of random selection. For that it is necessary to set up some
procedures or processes ensuring the parts in the specific population having similar number of
probabilities.
Question 4: ‘A Bit Dicey’
Dice Total $1 to play game refunded Additional $2 prize
Double AND (Total 8 or less) Yes No
Total more than 8 Yes Yes
Double AND (Total more than 8) No Yes
Everything else No No
a)
Probability is considered as the suitable and relevant method.
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
b) Also use a Venn diagram to illustrate the outcomes of events in Sammy’s game of chance.
0.27 0.38
0.77

c) Calculate the probabilities of each of the events in Sammy’s game occurring.
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
A) 28/36 = 0.77
B) 10/36 = 0.27
C) 14/36 = 0.38
d)
According to me, the game played by Sammy was fair enough for participating in the community
program of the school.
E)
As per me, the game was fair enough and there were 36 possibilities on an overall basis. The same
number of it were 6, that are (1,1) (2,2) (3,3) (4,4) (5,5) (6,6)
Question 5
A) 63 0
90 4 1
B) P= 63/90 = 0.7
C) Q= 1- 0.7 =0.3
According to the formula of probability,
nCr pr qn-r
N= trials
R = successes
B) N= 10, c = 7
= 10C7 (0.7)7 (0.3)3
= 3 * 0.0823 * 0.027
=0.0066
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
A) 28/36 = 0.77
B) 10/36 = 0.27
C) 14/36 = 0.38
d)
According to me, the game played by Sammy was fair enough for participating in the community
program of the school.
E)
As per me, the game was fair enough and there were 36 possibilities on an overall basis. The same
number of it were 6, that are (1,1) (2,2) (3,3) (4,4) (5,5) (6,6)
Question 5
A) 63 0
90 4 1
B) P= 63/90 = 0.7
C) Q= 1- 0.7 =0.3
According to the formula of probability,
nCr pr qn-r
N= trials
R = successes
B) N= 10, c = 7
= 10C7 (0.7)7 (0.3)3
= 3 * 0.0823 * 0.027
=0.0066
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

1 out of 10
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.