BEA1009 Introduction to Quantitative Methods Assignment - Semester 1
VerifiedAdded on 2022/12/27
|11
|1109
|21
Homework Assignment
AI Summary
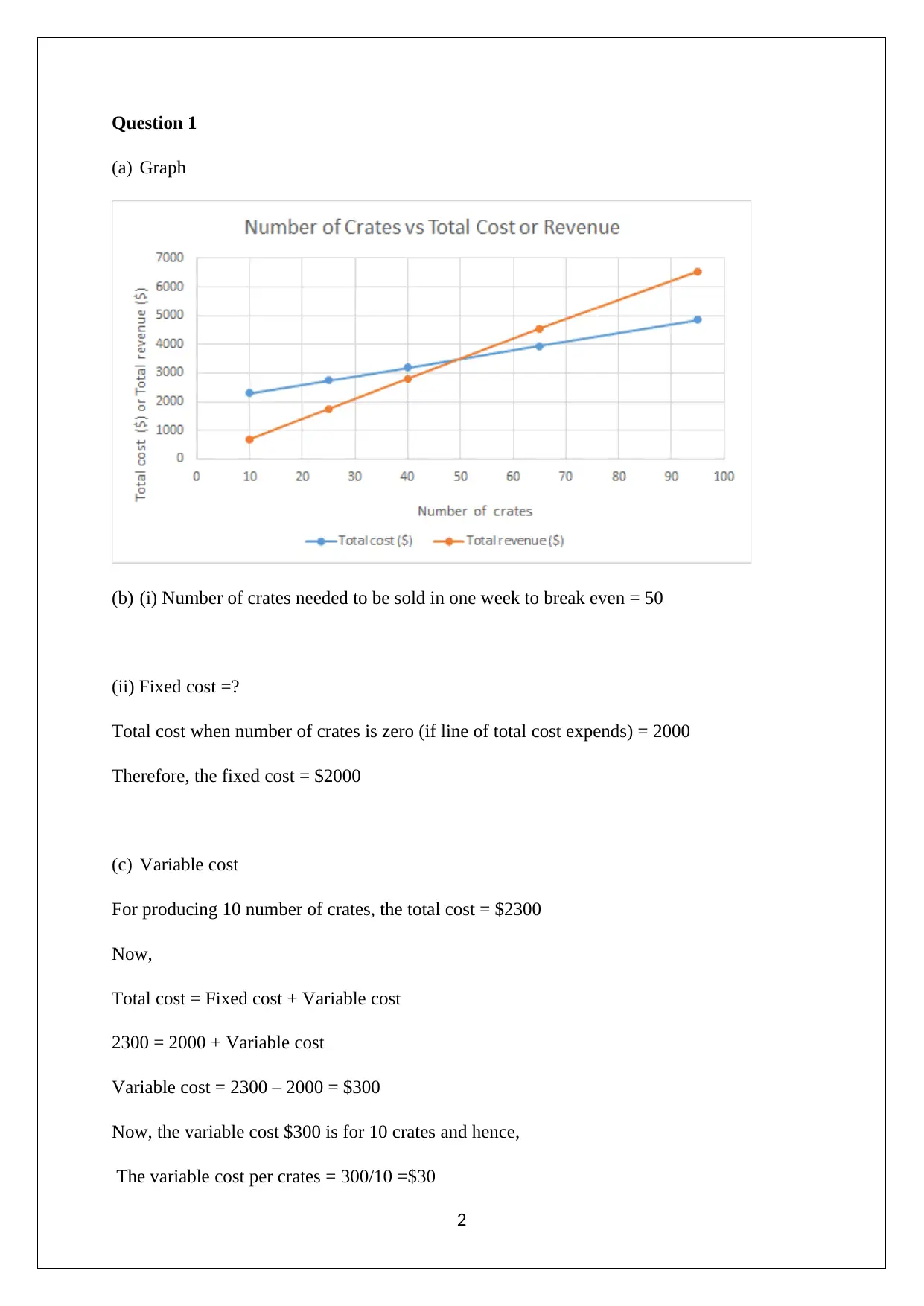
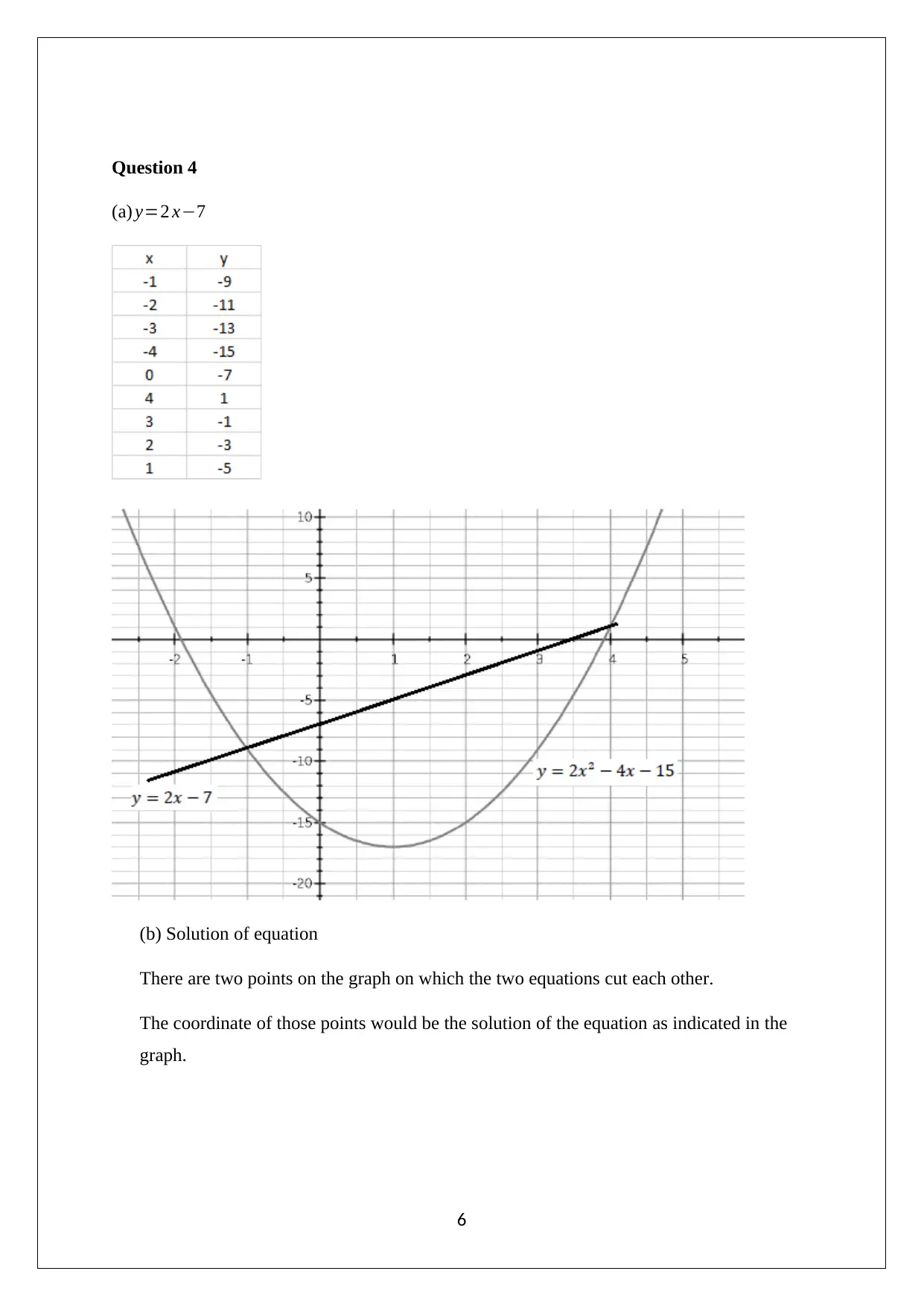
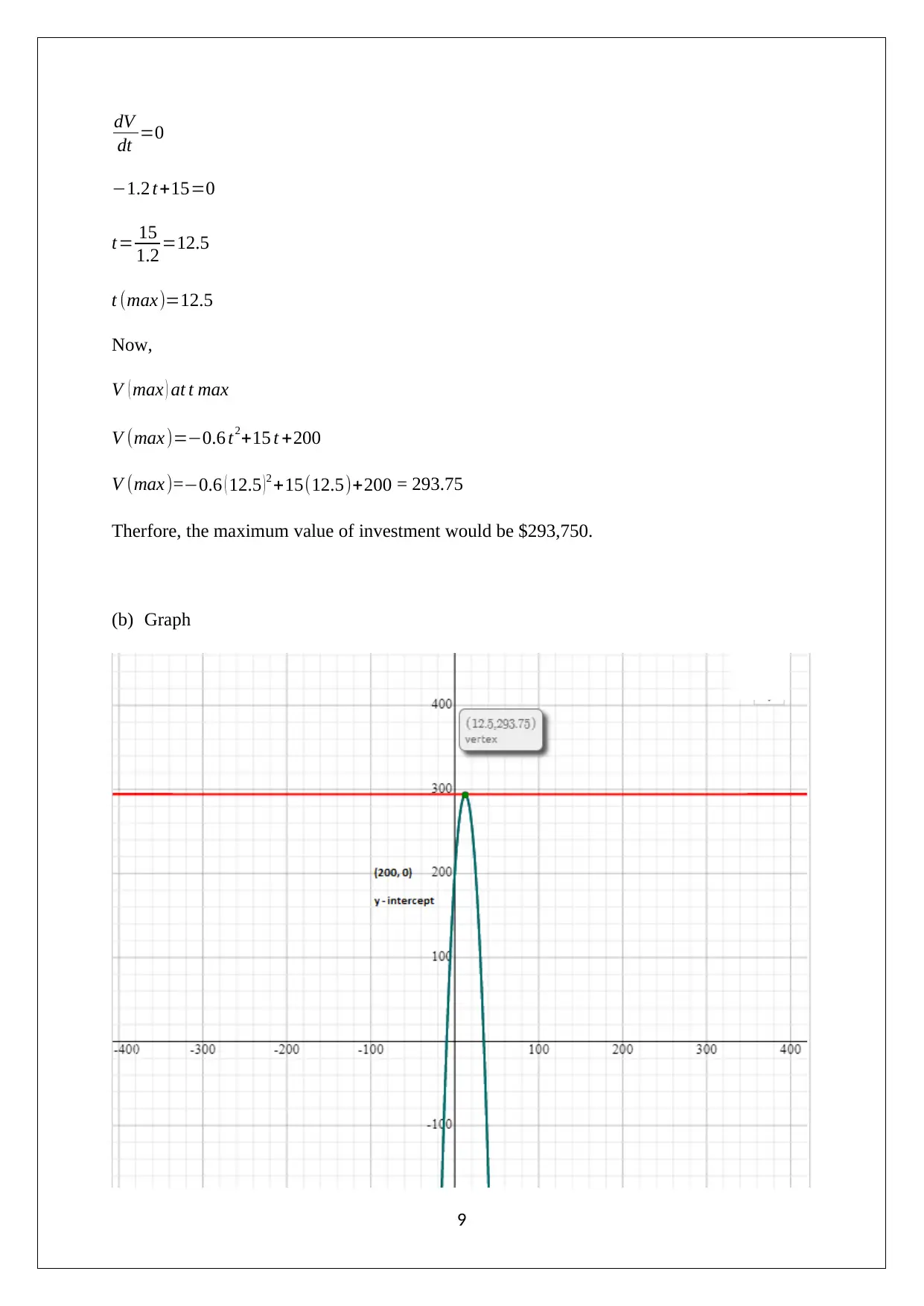
This document presents a comprehensive solution to a maths assignment covering various topics within quantitative methods. The assignment includes graphical analysis, such as plotting and interpreting graphs, and solving equations, including quadratic equations, and simultaneous equations. It also addresses business-related problems, such as break-even analysis, cost calculations, and the application of regression analysis. Furthermore, the solution delves into optimization problems involving finding the maximum value of an investment and geometric problems like area calculations. The solutions are detailed, showing all workings and steps to arrive at the final answers, which makes the assignment a valuable resource for students studying quantitative methods. The assignment covers learning objectives from 5.1 to 7.6.
1 out of 11













![[object Object]](/_next/static/media/star-bottom.7253800d.svg)