MATHS: Chaos and Dynamical Systems, Midterm 1 Assignment Solutions
VerifiedAdded on 2023/01/13
|22
|3968
|90
Homework Assignment
AI Summary
This document presents a detailed solution to a Maths assignment focusing on Chaos and Dynamical Systems. The assignment explores several key concepts, including plotting graphs and finding fixed points for given maps, determining whether fixed points are sinks or sources, and identifying the basin of attraction. It also covers finding parameters for a function to exhibit a 3-cycle, computing Lyapunov numbers, and identifying the type of bifurcation. Further, it addresses the location of periodic orbits for a given function and calculating the number of unique 7-periodic orbits. The solutions include detailed calculations and explanations of the concepts involved, providing a comprehensive understanding of the topics covered in the assignment. This resource, contributed by a student and published on Desklib, is designed to assist students with their studies, offering valuable insights and guidance for similar assignments.

MATHS
Student Name:
Register Number:
Submission Date:
Student Name:
Register Number:
Submission Date:
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Table of Contents
Question 1........................................................................................................................................................................ 1
a).................................................................................................................................................................................. 1
The basin attractor boundary of the fixed point is sink........................................................................................................4
Question 2........................................................................................................................................................................ 5
Question 3........................................................................................................................................................................ 6
Question 4........................................................................................................................................................................ 8
Question 5........................................................................................................................................................................ 9
Question 6...................................................................................................................................................................... 10
Question 7...................................................................................................................................................................... 10
Question 8...................................................................................................................................................................... 11
Question 9...................................................................................................................................................................... 12
Question 10.................................................................................................................................................................... 13
Question 11.................................................................................................................................................................... 13
Question 12.................................................................................................................................................................... 14
Question 13.................................................................................................................................................................... 14
Question 14.................................................................................................................................................................... 18
References...................................................................................................................................................................... 19
Question 1........................................................................................................................................................................ 1
a).................................................................................................................................................................................. 1
The basin attractor boundary of the fixed point is sink........................................................................................................4
Question 2........................................................................................................................................................................ 5
Question 3........................................................................................................................................................................ 6
Question 4........................................................................................................................................................................ 8
Question 5........................................................................................................................................................................ 9
Question 6...................................................................................................................................................................... 10
Question 7...................................................................................................................................................................... 10
Question 8...................................................................................................................................................................... 11
Question 9...................................................................................................................................................................... 12
Question 10.................................................................................................................................................................... 13
Question 11.................................................................................................................................................................... 13
Question 12.................................................................................................................................................................... 14
Question 13.................................................................................................................................................................... 14
Question 14.................................................................................................................................................................... 18
References...................................................................................................................................................................... 19
Question 1
a)
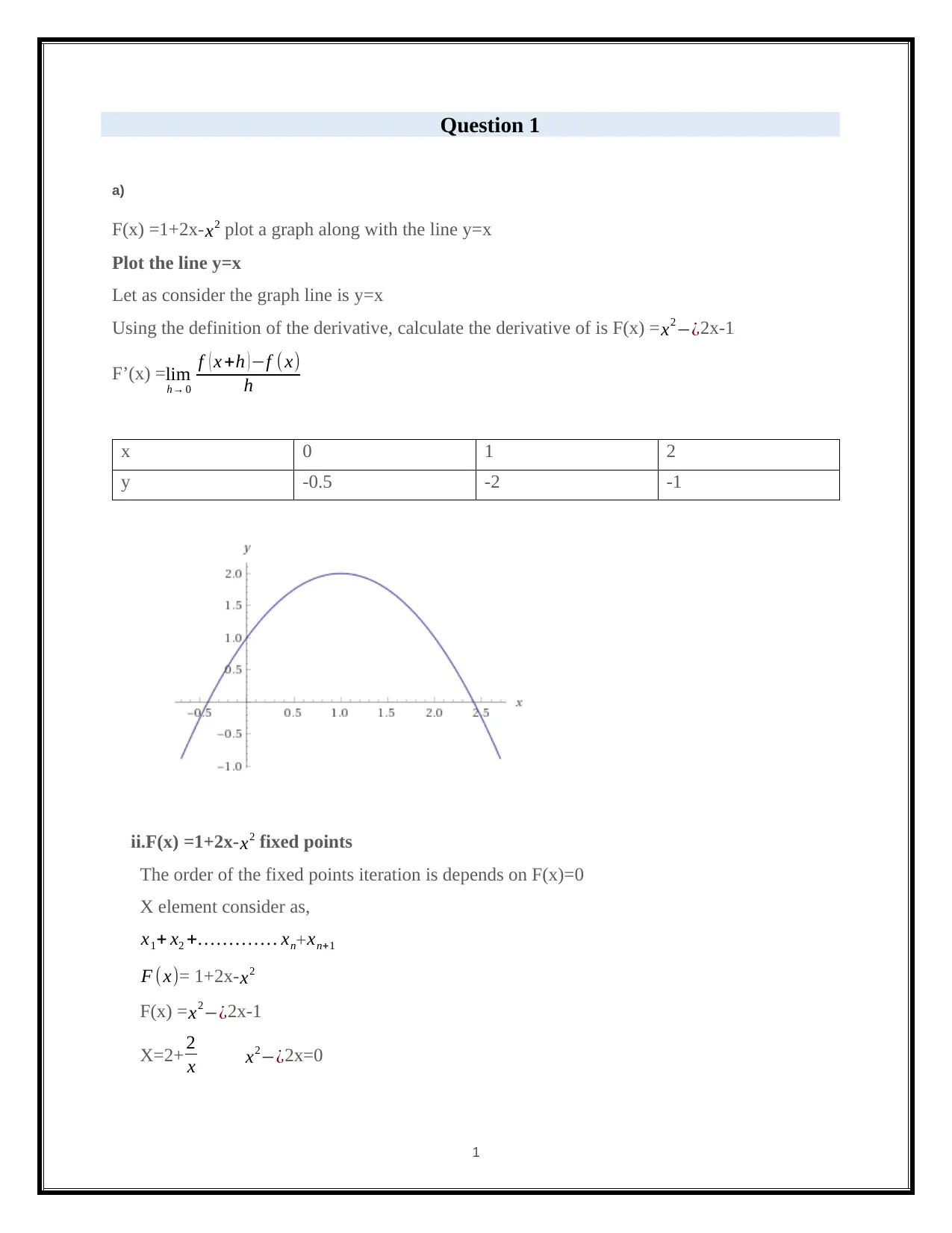
F(x) =1+2x- x2 plot a graph along with the line y=x
Plot the line y=x
Let as consider the graph line is y=x
Using the definition of the derivative, calculate the derivative of is F(x) =x2−¿2x-1
F’(x) =lim
h→ 0
f ( x +h )−f (x)
h
x 0 1 2
y -0.5 -2 -1
ii.F(x) =1+2x- x2 fixed points
The order of the fixed points iteration is depends on F(x)=0
X element consider as,
x1+ x2 +… … … … . xn+xn+1
F (x)= 1+2x- x2
F(x) = x2−¿2x-1
X=2+ 2
x x2−¿2x=0
1
a)
F(x) =1+2x- x2 plot a graph along with the line y=x
Plot the line y=x
Let as consider the graph line is y=x
Using the definition of the derivative, calculate the derivative of is F(x) =x2−¿2x-1
F’(x) =lim
h→ 0
f ( x +h )−f (x)
h
x 0 1 2
y -0.5 -2 -1
ii.F(x) =1+2x- x2 fixed points
The order of the fixed points iteration is depends on F(x)=0
X element consider as,
x1+ x2 +… … … … . xn+xn+1
F (x)= 1+2x- x2
F(x) = x2−¿2x-1
X=2+ 2
x x2−¿2x=0
1
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

xn+2=2+ 2
xn
x(x-2)=0
x 1=1 xn+2= 1
xn −2
X2=2+ 2
1=4 x2= 1
2.7−2 =1.428
X3=2+ 2
4 =2.5 x3=-1.666
X4=2.8 x4=-0.27
X5=2.714 x5=-0.57
X6=2.736 x6=-.089
G(x) =1+1/x xn+2= 1
xn −2
G’(x) =1/- x2 g(x) = 1
x−2
G’(x) = ( 1+ √5
2 ) g’(x) = 1
( x−2)2 =
1
( 1+ √ 5
2 )−2 ¿
2 ¿=7.1818>1
G’(x) =
1
( 1+ √5
2 )
2
=-0.3819660
|-0.3819660|<1
Fixed point is(0.38, 7.18)
Remember that xn+2=g(x)
If |g’(r)|<1coverage
If g’(r) =0 coverage quadratic
G’’(r) =0 coverage order 3
(iii)F(x) =1+2x- x2 determine whether they are sinks or sources,
The fixed point of F by solving F(x) = 1+2x-x2 get 0 and 7 fixed point of F.
The period of the two points are found among the fixed points of the map f 2. The fixed point of F
is not period two points.
F(x) = 1+2x-x2
2
xn
x(x-2)=0
x 1=1 xn+2= 1
xn −2
X2=2+ 2
1=4 x2= 1
2.7−2 =1.428
X3=2+ 2
4 =2.5 x3=-1.666
X4=2.8 x4=-0.27
X5=2.714 x5=-0.57
X6=2.736 x6=-.089
G(x) =1+1/x xn+2= 1
xn −2
G’(x) =1/- x2 g(x) = 1
x−2
G’(x) = ( 1+ √5
2 ) g’(x) = 1
( x−2)2 =
1
( 1+ √ 5
2 )−2 ¿
2 ¿=7.1818>1
G’(x) =
1
( 1+ √5
2 )
2
=-0.3819660
|-0.3819660|<1
Fixed point is(0.38, 7.18)
Remember that xn+2=g(x)
If |g’(r)|<1coverage
If g’(r) =0 coverage quadratic
G’’(r) =0 coverage order 3
(iii)F(x) =1+2x- x2 determine whether they are sinks or sources,
The fixed point of F by solving F(x) = 1+2x-x2 get 0 and 7 fixed point of F.
The period of the two points are found among the fixed points of the map f 2. The fixed point of F
is not period two points.
F(x) = 1+2x-x2
2
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
F(x) = x2−¿2x-1
F2(x)=( x2−2 x−1)2= x4-4x2-1
The fixed point is 0 and 2
After simplification of the equation is
x4-4 x2-1 and x=0
Since 2 is the solution we can write as the equation is x-2 second degree of polynomial
is x4-4x2-1=x-2
¿ ¿-4 x2-1)(x-2)=0
(x-2)=0¿ ¿-4x2-1)=0
So {1 ± √2} is consider as {1+ √ 2 , 1− √ 2} we can consider F’ (1+ √2 ,) F(1− √2 ,)
Let as consider the value of y=4x-8
{4(1+ √2 ,)-8 , 4(1− √2 ,)-8}
Which is equal to the fixed point |-67| since the value is bigger than 1. We have a source period
of the fixed point values is sink.
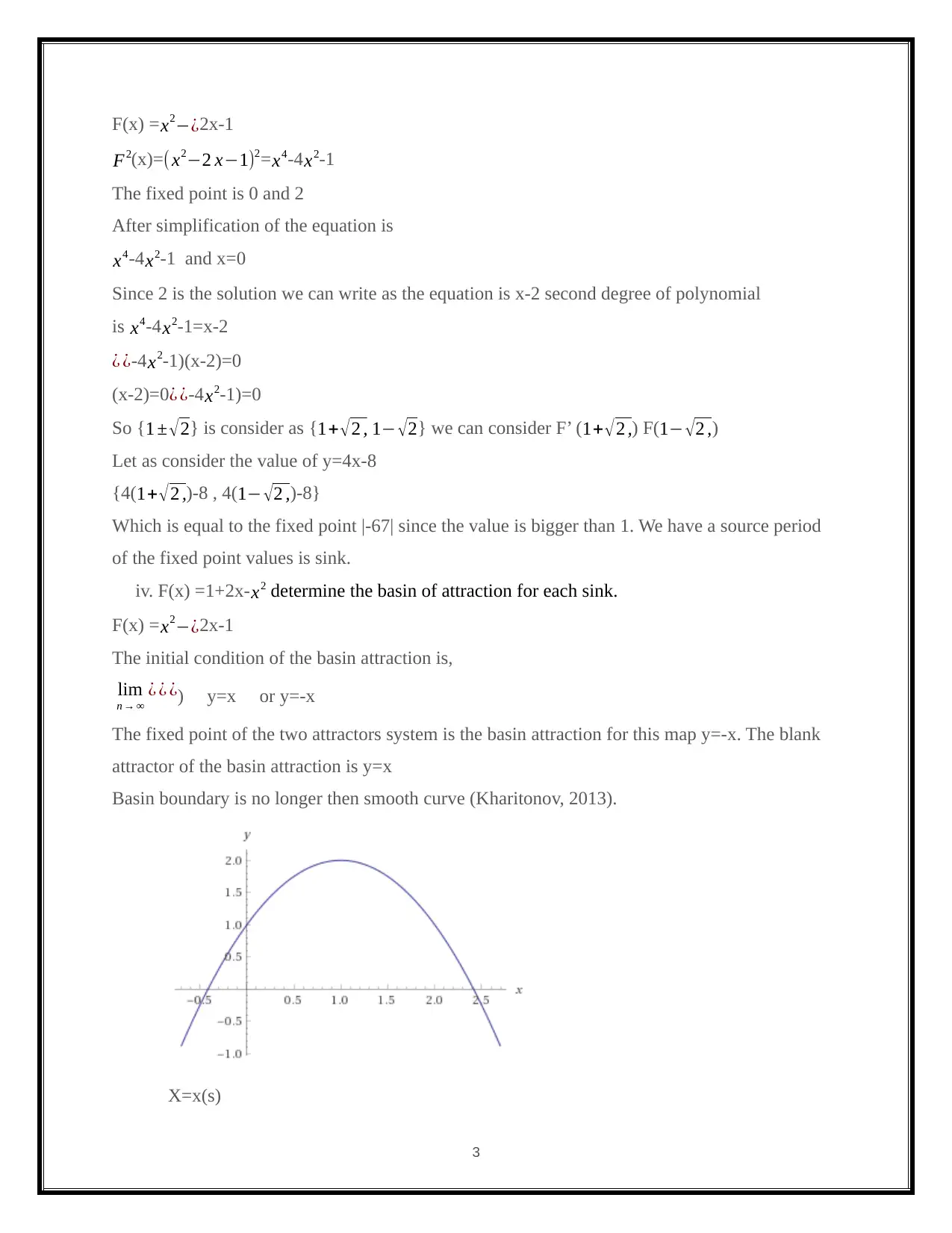
iv. F(x) =1+2x- x2 determine the basin of attraction for each sink.
F(x) = x2−¿2x-1
The initial condition of the basin attraction is,
lim
n → ∞
¿ ¿ ¿) y=x or y=-x
The fixed point of the two attractors system is the basin attraction for this map y=-x. The blank
attractor of the basin attraction is y=x
Basin boundary is no longer then smooth curve (Kharitonov, 2013).
X=x(s)
3
F2(x)=( x2−2 x−1)2= x4-4x2-1
The fixed point is 0 and 2
After simplification of the equation is
x4-4 x2-1 and x=0
Since 2 is the solution we can write as the equation is x-2 second degree of polynomial
is x4-4x2-1=x-2
¿ ¿-4 x2-1)(x-2)=0
(x-2)=0¿ ¿-4x2-1)=0
So {1 ± √2} is consider as {1+ √ 2 , 1− √ 2} we can consider F’ (1+ √2 ,) F(1− √2 ,)
Let as consider the value of y=4x-8
{4(1+ √2 ,)-8 , 4(1− √2 ,)-8}
Which is equal to the fixed point |-67| since the value is bigger than 1. We have a source period
of the fixed point values is sink.
iv. F(x) =1+2x- x2 determine the basin of attraction for each sink.
F(x) = x2−¿2x-1
The initial condition of the basin attraction is,
lim
n → ∞
¿ ¿ ¿) y=x or y=-x
The fixed point of the two attractors system is the basin attraction for this map y=-x. The blank
attractor of the basin attraction is y=x
Basin boundary is no longer then smooth curve (Kharitonov, 2013).
X=x(s)
3

X=x( x2−¿2x-1)
Y=y(s)
Y=y(x( x2−¿2x-1)) for 2>s>0
If s1≠ s 2
The basin attractor boundary of the fixed point is sink (Romeu and Vera‐Hernández, 2016).
b)
i. F(x) = 1/2+x+sin(x) plot the line graph y=x
F(x) = 1/2+x+sin(x)
F(x)= x +sin(x)+ ½
X=x+ 1
2 sin(x) =0
F(x) = 1/2+x+sin(x)
ii. fixed points
The fixed point of the values Is consider as
x1+ x2 +… … … … . xn+ xn+1
F(x)=x−¿ sin(x)- ½
The graph of g(x) and x value is,
Initially guest value is x0=2
i 0 1 2 3 4 5
Xi 1.409 1.487 1.496 1.496 1.497 1.497
G(x)= x+sin[x]+1/2 the fixed point values is 1.497
4
Y=y(s)
Y=y(x( x2−¿2x-1)) for 2>s>0
If s1≠ s 2
The basin attractor boundary of the fixed point is sink (Romeu and Vera‐Hernández, 2016).
b)
i. F(x) = 1/2+x+sin(x) plot the line graph y=x
F(x) = 1/2+x+sin(x)
F(x)= x +sin(x)+ ½
X=x+ 1
2 sin(x) =0
F(x) = 1/2+x+sin(x)
ii. fixed points
The fixed point of the values Is consider as
x1+ x2 +… … … … . xn+ xn+1
F(x)=x−¿ sin(x)- ½
The graph of g(x) and x value is,
Initially guest value is x0=2
i 0 1 2 3 4 5
Xi 1.409 1.487 1.496 1.496 1.497 1.497
G(x)= x+sin[x]+1/2 the fixed point values is 1.497
4
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

F(x) = 1/2+x+sin(x)
iii.determine whether they are sinks or sources,
∫ x +sin [x ]+1/2dx
∫ x +sin [x ]+1/2dx
= x
2 +cos [x ]+sin [x ]+1/2
The source and sink value is {1 ± √2} is consider as {1+ √ 2 , 1− √ 2}
F(x)=1/2+x+sin(x)
iv.determine the basin of attraction for each sink
The fixed point of the two attractors system is the basin attraction for this map y=-x. The blank
attractor of the basin attraction is y=x
Basin boundary is no longer then smooth curve.
X=x(s)
X=x(1+ √2 , )
Y=y(s)
Y=y(x(1+ √2 , )) for 2>s>0
If s1 ≠ s 2
The basin attractor boundary of the fixed point is sink.
c)
i.
{ x ln x x ≠ 0
o x=0
i.plot y=x
F(x)=x
ii. fixed point (0.1)
iii. Sink and source can be denoted the sink value is constant
iv.
5
iii.determine whether they are sinks or sources,
∫ x +sin [x ]+1/2dx
∫ x +sin [x ]+1/2dx
= x
2 +cos [x ]+sin [x ]+1/2
The source and sink value is {1 ± √2} is consider as {1+ √ 2 , 1− √ 2}
F(x)=1/2+x+sin(x)
iv.determine the basin of attraction for each sink
The fixed point of the two attractors system is the basin attraction for this map y=-x. The blank
attractor of the basin attraction is y=x
Basin boundary is no longer then smooth curve.
X=x(s)
X=x(1+ √2 , )
Y=y(s)
Y=y(x(1+ √2 , )) for 2>s>0
If s1 ≠ s 2
The basin attractor boundary of the fixed point is sink.
c)
i.
{ x ln x x ≠ 0
o x=0
i.plot y=x
F(x)=x
ii. fixed point (0.1)
iii. Sink and source can be denoted the sink value is constant
iv.
5
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

{1 ± √2} is consider as {1+ √ 2 , 1− √ 2} we can consider F’ (1+ √2 ,) F(1− √2 ,)
Let as consider the value of y=1
{4(1+ √2 ,)-1 , 4(1− √2 ,)-1}
Which is equal to the fixed point |-1| since the value is bigger than 1. We have a source period of
the fixed point values is sink.
Question 2
F(x)=a+bx+c x2
We can assume the 3 cycle value is, (0,1,2)
F(x)= a+bx+cx2
a, b, c is the numerical constant value. But c is not equal to zero
y= a+bx+c x2 +d x3
y= a+bx+c x2 +d x3+ ¿ e x4
x= −b ± √ b2−4 ac
2a
Trajectory values is {0,1,2,0,1,2}
6
Let as consider the value of y=1
{4(1+ √2 ,)-1 , 4(1− √2 ,)-1}
Which is equal to the fixed point |-1| since the value is bigger than 1. We have a source period of
the fixed point values is sink.
Question 2
F(x)=a+bx+c x2
We can assume the 3 cycle value is, (0,1,2)
F(x)= a+bx+cx2
a, b, c is the numerical constant value. But c is not equal to zero
y= a+bx+c x2 +d x3
y= a+bx+c x2 +d x3+ ¿ e x4
x= −b ± √ b2−4 ac
2a
Trajectory values is {0,1,2,0,1,2}
6
X=0, x=1, x=2
γ=t+x
γ=t+ x1
γ=t+ x2
γ=t+ x3
γ =0+ x1, 1+ x2 , 2+ x3
The lyapunov number of value 0 is map, of (0,1, 2) is the periodic sink.
Question 3
F(x)=1+x+asin(x)
a=1
Let as find the value of x=-b ± √ 1−c
X=−x ± √1−sin ( x)
2 X 1
7
γ=t+x
γ=t+ x1
γ=t+ x2
γ=t+ x3
γ =0+ x1, 1+ x2 , 2+ x3
The lyapunov number of value 0 is map, of (0,1, 2) is the periodic sink.
Question 3
F(x)=1+x+asin(x)
a=1
Let as find the value of x=-b ± √ 1−c
X=−x ± √1−sin ( x)
2 X 1
7
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

X= √1−sin (1)
2 X 1 =[0,1]
The bifurcation value is,
C=3.079
Question 4
F(x) =ax(1-x)
To find the value of a=1 to apply the value is,
F’(x) = ax(1-x)
F’(x) =ax-x2
F’(x) =A(x- x2)
X=1
a=ax (1-1)=0
λ=5
8
2 X 1 =[0,1]
The bifurcation value is,
C=3.079
Question 4
F(x) =ax(1-x)
To find the value of a=1 to apply the value is,
F’(x) = ax(1-x)
F’(x) =ax-x2
F’(x) =A(x- x2)
X=1
a=ax (1-1)=0
λ=5
8
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
F(x),f 2(x),f 3(x),f 4(x) the function of 2n fixed point value is,
p N(p)
1 2
2 1
3 2
4 3
N(p)= 1
p (2p- ∑
divide
k X N ( k)
N(p)= 1
p e phT
hT = lim
p → ∞
¿ ¿=log ¿ ¿=)
1
p (log( 2p / p))=log(2)- 1
p log(p)
9
p N(p)
1 2
2 1
3 2
4 3
N(p)= 1
p (2p- ∑
divide
k X N ( k)
N(p)= 1
p e phT
hT = lim
p → ∞
¿ ¿=log ¿ ¿=)
1
p (log( 2p / p))=log(2)- 1
p log(p)
9

1
p (log (25 /5))=log (2)- 1
5log(5)
Stage 1 N(p) Stage 2 N(p) Stage 3 N(p)
5 6 15 2182 25 1342176
Question 5
F(x)=4x(1-x) to find the 7 periodic orbit value is
F(x)= 4x-4x2
F(x) =x(4-4x)=4x(1- x2)=4(x- x2)=4x
We can calculating the 7 periodic value is,
F(x),f 2(x),f 3(x),f 4(x),f 5(x), f 6(x)
To find the diagonal of value y=x
F(x) periodic value is,
D(x)=4x(1-x)
dx
dt =4x(1-x)
dx
dt =4 x 1
2(1- 1
2)=1
X(t)=(t+T) of the interval value is[0,T]
N(p)= 1
p (2p- ∑
divide
k X N ( k)
= 1
p log (2 p
p )=log(2)- 1
p (log(p))
1
27 log ( 2 X 27
27 )=log(2)- 1
27 (log(27))=4971008
Question 6
F(x)= 4x(1-x)
Interval of the point itinerary is LRRRLRL
Find the decimal place value is 5
F(x)= 4x(1-x)
10
p (log (25 /5))=log (2)- 1
5log(5)
Stage 1 N(p) Stage 2 N(p) Stage 3 N(p)
5 6 15 2182 25 1342176
Question 5
F(x)=4x(1-x) to find the 7 periodic orbit value is
F(x)= 4x-4x2
F(x) =x(4-4x)=4x(1- x2)=4(x- x2)=4x
We can calculating the 7 periodic value is,
F(x),f 2(x),f 3(x),f 4(x),f 5(x), f 6(x)
To find the diagonal of value y=x
F(x) periodic value is,
D(x)=4x(1-x)
dx
dt =4x(1-x)
dx
dt =4 x 1
2(1- 1
2)=1
X(t)=(t+T) of the interval value is[0,T]
N(p)= 1
p (2p- ∑
divide
k X N ( k)
= 1
p log (2 p
p )=log(2)- 1
p (log(p))
1
27 log ( 2 X 27
27 )=log(2)- 1
27 (log(27))=4971008
Question 6
F(x)= 4x(1-x)
Interval of the point itinerary is LRRRLRL
Find the decimal place value is 5
F(x)= 4x(1-x)
10
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 22
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.




