MATLAB Homework: Intracranial Pressure and EOG Signal Analysis
VerifiedAdded on 2022/09/09
|13
|1310
|15
Homework Assignment
AI Summary
This MATLAB homework assignment addresses two main problems. The first involves analyzing a system's response to different input injections, modeling intracranial pressure using a transfer function, and calculating compliance. The solution includes MATLAB code to simulate the system's behavior, generate plots for varying injection volumes, and calculate compliance values. The second problem focuses on processing an electrooculogram (EOG) signal. The solution involves loading EOG data, calculating statistical properties like mean and power, and performing a Fourier transform to analyze the signal's frequency spectrum. The provided MATLAB code calculates the mean, power, and power spectral density of the EOG signal, along with the frequency at which maximum power occurs, providing a comprehensive analysis of the signal's characteristics and the system parameters.

Running head: MATLAB Homework
MATLAB Homework
Name of the Student
Name of the University
Author Note
MATLAB Homework
Name of the Student
Name of the University
Author Note
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

1MATLAB Homework
9.1:
Given, input-output equation is
τdΔP ( t )
dt + ΔP ( t ) =kr ( t )
Now, taking Laplace transform of the equation we get,
τ s ΔP ( s ) + ΔP ( s ) =k∗R (s)
=> ΔP ( s )
R ( s ) = k
τs+1
a) Now, from the figure 31 given that,
For ΔV = 0.1,0.2,0.3 and 0.4 mL injection is on ton = 15 secs and stays for 2,4,6 and 8 secs
respectively. The amplitude of signal r(t) = 0.05 mL/sec or 5 mmHg.
MATLAB code:
t = 0:1:180;
k = 55; tao = 66;P0 = 0.12; % Assuming system parameters
sys = tf(k,[tao,1]); % transfer function
%% delV = 0.1 mL or injection time = 2 secs.
r = zeros(1,length(t));
r(16:18) = 0.05;
P = lsim(sys,r,t); P = P + P0;
9.1:
Given, input-output equation is
τdΔP ( t )
dt + ΔP ( t ) =kr ( t )
Now, taking Laplace transform of the equation we get,
τ s ΔP ( s ) + ΔP ( s ) =k∗R (s)
=> ΔP ( s )
R ( s ) = k
τs+1
a) Now, from the figure 31 given that,
For ΔV = 0.1,0.2,0.3 and 0.4 mL injection is on ton = 15 secs and stays for 2,4,6 and 8 secs
respectively. The amplitude of signal r(t) = 0.05 mL/sec or 5 mmHg.
MATLAB code:
t = 0:1:180;
k = 55; tao = 66;P0 = 0.12; % Assuming system parameters
sys = tf(k,[tao,1]); % transfer function
%% delV = 0.1 mL or injection time = 2 secs.
r = zeros(1,length(t));
r(16:18) = 0.05;
P = lsim(sys,r,t); P = P + P0;

2MATLAB Homework
figure(1)
plot(t,P,'b-')
hold on
plot(t,r,'r-')
xlabel('Time in sec')
ylabel('Intracranial pressure in mmHg')
title('P(t) vs t and r(t) vs t')
grid on
legend('P(t)','r(t)')
hold off
%% delV = 0.2 mL or injection time = 4 secs.
r = zeros(1,length(t));
r(16:20) = 0.05;
P = lsim(sys,r,t); P = P + P0;
figure(2)
plot(t,P)
hold on
plot(t,r)
figure(1)
plot(t,P,'b-')
hold on
plot(t,r,'r-')
xlabel('Time in sec')
ylabel('Intracranial pressure in mmHg')
title('P(t) vs t and r(t) vs t')
grid on
legend('P(t)','r(t)')
hold off
%% delV = 0.2 mL or injection time = 4 secs.
r = zeros(1,length(t));
r(16:20) = 0.05;
P = lsim(sys,r,t); P = P + P0;
figure(2)
plot(t,P)
hold on
plot(t,r)
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

3MATLAB Homework
xlabel('Time in sec')
ylabel('Intracranial pressure in mmHg')
title('P(t) vs t and r(t) vs t')
legend('P(t)','r(t)')
grid on
hold off
%% delV = 0.3 mL or injection time = 6 secs.
r = zeros(1,length(t));
r(16:22) = 0.05;
P = lsim(sys,r,t); P = P + P0;
figure(3)
plot(t,P)
hold on
plot(t,r)
xlabel('Time in sec')
ylabel('Intracranial pressure in mmHg')
title('P(t) vs t and r(t) vs t')
grid on
xlabel('Time in sec')
ylabel('Intracranial pressure in mmHg')
title('P(t) vs t and r(t) vs t')
legend('P(t)','r(t)')
grid on
hold off
%% delV = 0.3 mL or injection time = 6 secs.
r = zeros(1,length(t));
r(16:22) = 0.05;
P = lsim(sys,r,t); P = P + P0;
figure(3)
plot(t,P)
hold on
plot(t,r)
xlabel('Time in sec')
ylabel('Intracranial pressure in mmHg')
title('P(t) vs t and r(t) vs t')
grid on
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

4MATLAB Homework
legend('P(t)','r(t)')
hold off
%% delV = 0.4 mL or injection time = 8 secs.
r = zeros(1,length(t));
r(16:24) = 0.05;
P = lsim(sys,r,t); P = P + P0;
figure(4)
plot(t,P)
hold on
plot(t,r)
xlabel('Time in sec')
ylabel('Intracranial pressure in mmHg')
title('P(t) vs t and r(t) vs t')
grid on
legend('P(t)','r(t)')
hold off
legend('P(t)','r(t)')
hold off
%% delV = 0.4 mL or injection time = 8 secs.
r = zeros(1,length(t));
r(16:24) = 0.05;
P = lsim(sys,r,t); P = P + P0;
figure(4)
plot(t,P)
hold on
plot(t,r)
xlabel('Time in sec')
ylabel('Intracranial pressure in mmHg')
title('P(t) vs t and r(t) vs t')
grid on
legend('P(t)','r(t)')
hold off
5MATLAB Homework
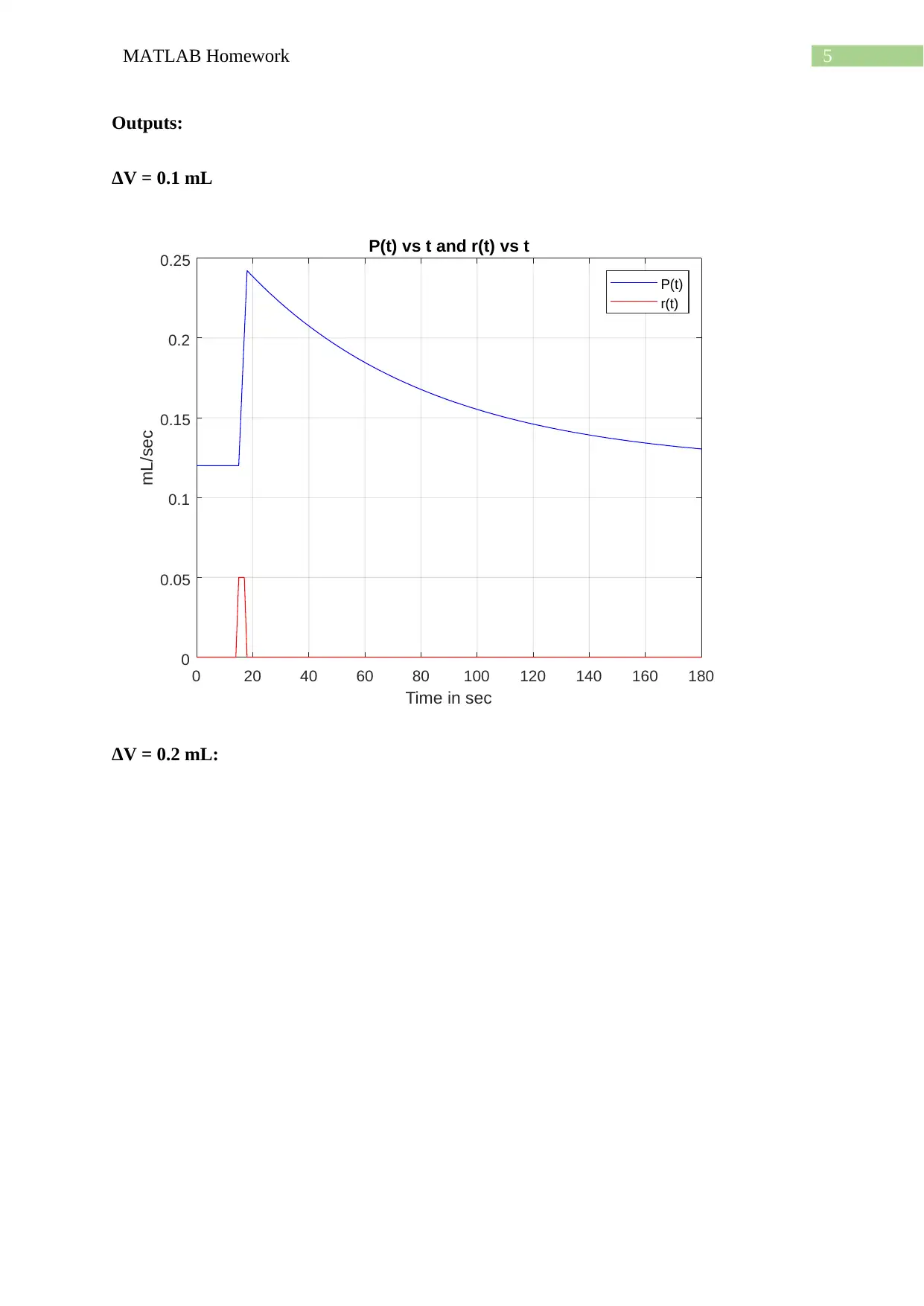
Outputs:
ΔV = 0.1 mL
0 20 40 60 80 100 120 140 160 180
Time in sec
0
0.05
0.1
0.15
0.2
0.25
mL/sec
P(t) vs t and r(t) vs t
P(t)
r(t)
ΔV = 0.2 mL:
Outputs:
ΔV = 0.1 mL
0 20 40 60 80 100 120 140 160 180
Time in sec
0
0.05
0.1
0.15
0.2
0.25
mL/sec
P(t) vs t and r(t) vs t
P(t)
r(t)
ΔV = 0.2 mL:
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
6MATLAB Homework
0 20 40 60 80 100 120 140 160 180
Time in sec
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
mL/sec
P(t) vs t and r(t) vs t
P(t)
r(t)
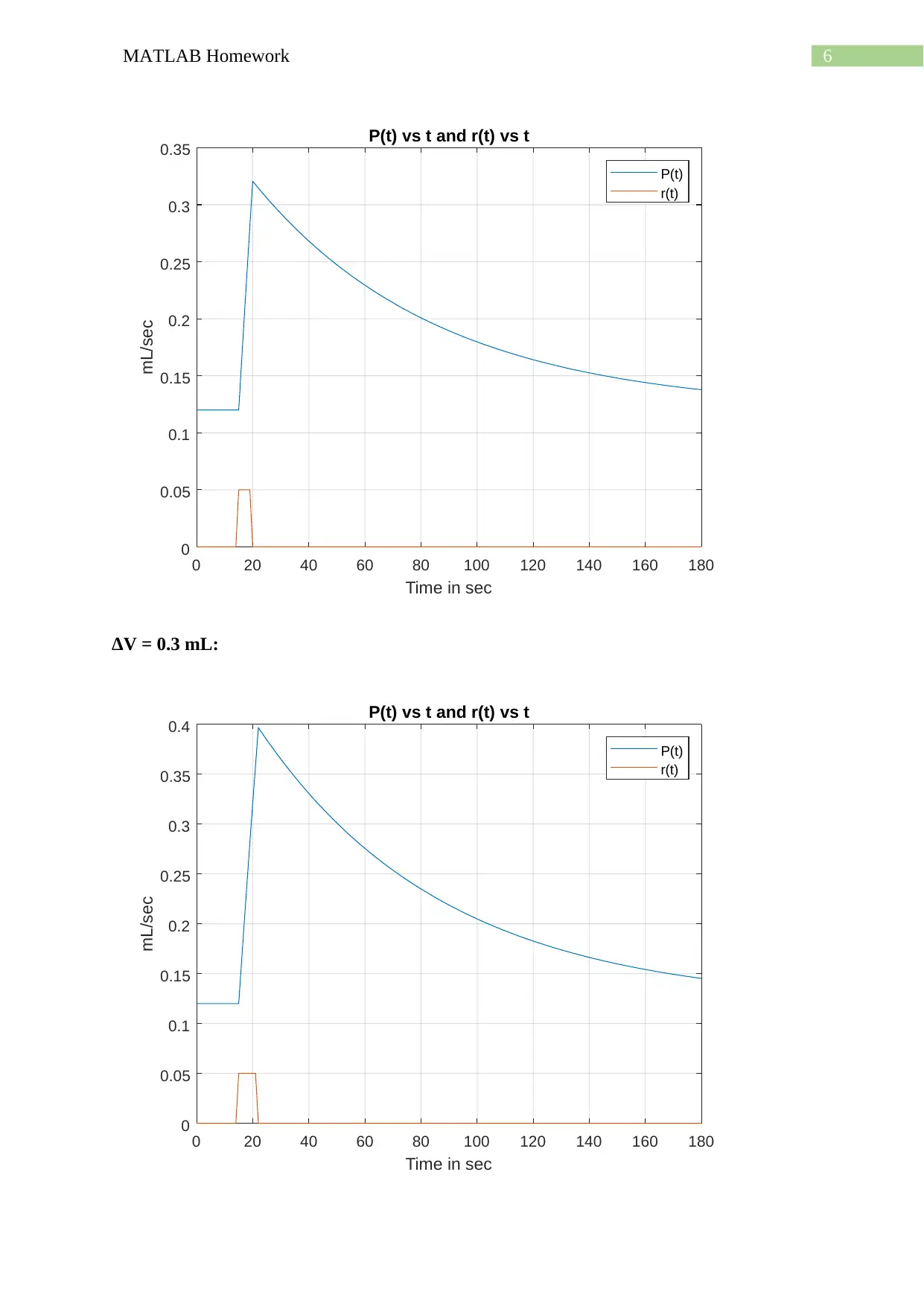
ΔV = 0.3 mL:
0 20 40 60 80 100 120 140 160 180
Time in sec
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
mL/sec
P(t) vs t and r(t) vs t
P(t)
r(t)
0 20 40 60 80 100 120 140 160 180
Time in sec
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
mL/sec
P(t) vs t and r(t) vs t
P(t)
r(t)
ΔV = 0.3 mL:
0 20 40 60 80 100 120 140 160 180
Time in sec
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
mL/sec
P(t) vs t and r(t) vs t
P(t)
r(t)
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
7MATLAB Homework
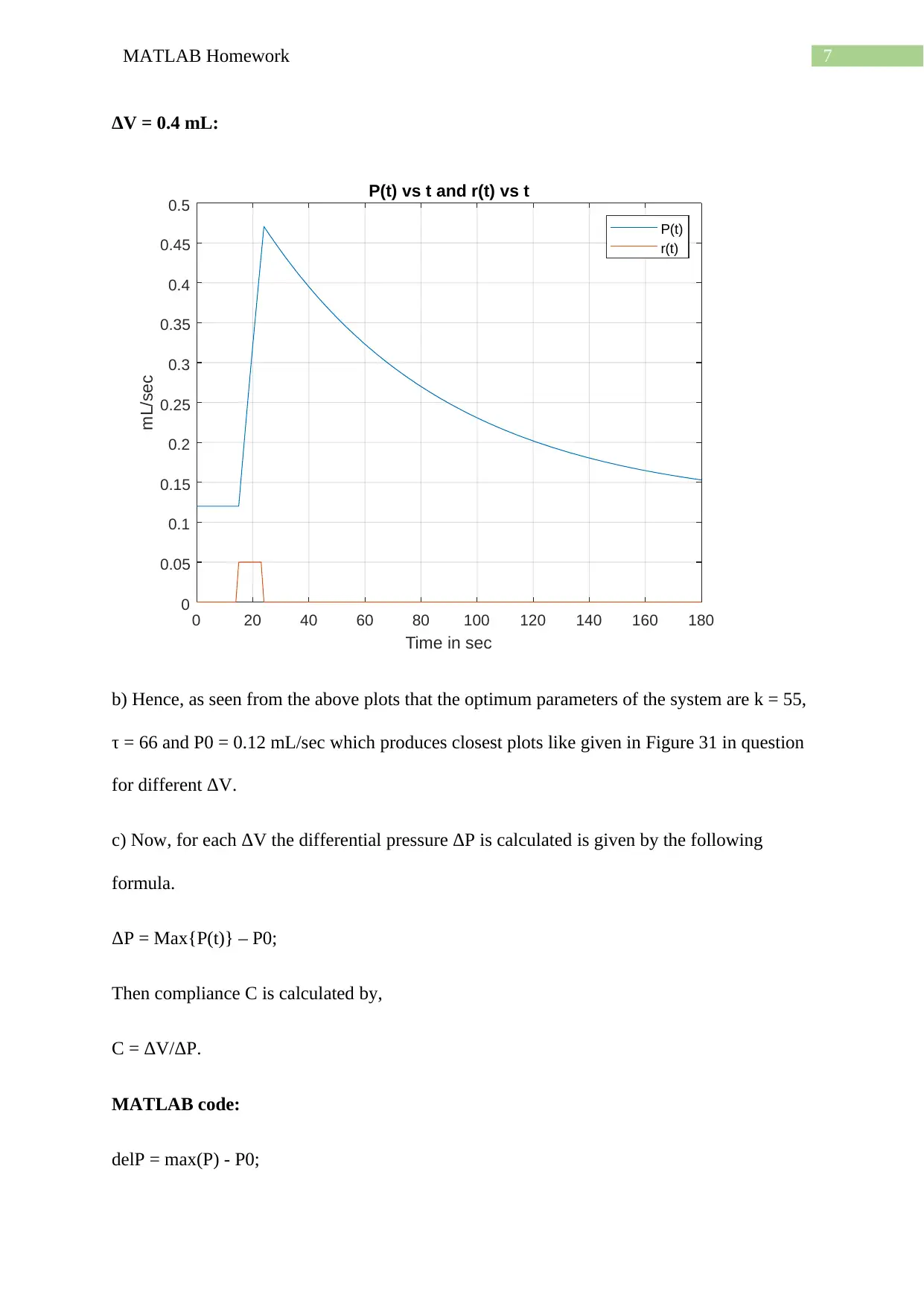
ΔV = 0.4 mL:
0 20 40 60 80 100 120 140 160 180
Time in sec
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
0.5
mL/sec
P(t) vs t and r(t) vs t
P(t)
r(t)
b) Hence, as seen from the above plots that the optimum parameters of the system are k = 55,
τ = 66 and P0 = 0.12 mL/sec which produces closest plots like given in Figure 31 in question
for different ΔV.
c) Now, for each ΔV the differential pressure ΔP is calculated is given by the following
formula.
ΔP = Max{P(t)} – P0;
Then compliance C is calculated by,
C = ΔV/ΔP.
MATLAB code:
delP = max(P) - P0;
ΔV = 0.4 mL:
0 20 40 60 80 100 120 140 160 180
Time in sec
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
0.5
mL/sec
P(t) vs t and r(t) vs t
P(t)
r(t)
b) Hence, as seen from the above plots that the optimum parameters of the system are k = 55,
τ = 66 and P0 = 0.12 mL/sec which produces closest plots like given in Figure 31 in question
for different ΔV.
c) Now, for each ΔV the differential pressure ΔP is calculated is given by the following
formula.
ΔP = Max{P(t)} – P0;
Then compliance C is calculated by,
C = ΔV/ΔP.
MATLAB code:
delP = max(P) - P0;

8MATLAB Homework
delv = 0.1;
C = delv/delP;
fprintf('At delV =%.1f mL delP = %.2f mL/sec and Compliance C = %.2f mL/mmHg\
n',delv,delP,C)
delP = max(P) - P0;
delv = 0.2;
C = delv/delP;
fprintf('At delV =%.1f mL delP = %.2f mL/sec and Compliance C = %.2f mL/mmHg\
n',delv,delP,C)
delP = max(P) - P0;
delv = 0.3;
C = delv/delP;
fprintf('At delV =%.1f mL delP = %.2f mL/sec and Compliance C = %.2f mL/mmHg\
n',delv,delP,C)
delP = max(P) - P0;
delv = 0.4;
C = delv/delP;
fprintf('At delV =%.1f mL delP = %.2f mL/sec and Compliance C = %.2f mL/mmHg\
n',delv,delP,C)
Output:
At delV =0.1 mL delP = 0.12 mL/sec and Compliance C = 0.82 mL/mmHg
delv = 0.1;
C = delv/delP;
fprintf('At delV =%.1f mL delP = %.2f mL/sec and Compliance C = %.2f mL/mmHg\
n',delv,delP,C)
delP = max(P) - P0;
delv = 0.2;
C = delv/delP;
fprintf('At delV =%.1f mL delP = %.2f mL/sec and Compliance C = %.2f mL/mmHg\
n',delv,delP,C)
delP = max(P) - P0;
delv = 0.3;
C = delv/delP;
fprintf('At delV =%.1f mL delP = %.2f mL/sec and Compliance C = %.2f mL/mmHg\
n',delv,delP,C)
delP = max(P) - P0;
delv = 0.4;
C = delv/delP;
fprintf('At delV =%.1f mL delP = %.2f mL/sec and Compliance C = %.2f mL/mmHg\
n',delv,delP,C)
Output:
At delV =0.1 mL delP = 0.12 mL/sec and Compliance C = 0.82 mL/mmHg
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

9MATLAB Homework
At delV =0.2 mL delP = 0.20 mL/sec and Compliance C = 1.00 mL/mmHg
At delV =0.3 mL delP = 0.28 mL/sec and Compliance C = 1.08 mL/mmHg
At delV =0.4 mL delP = 0.35 mL/sec and Compliance C = 1.14 mL/mmHg
Hence, it can be seen that the compliance C is largest when ΔV =0.4 mL.
9.2:
MATLAB code:
load('eog_trimmed.mat');
figure(1)
plot(t,eog)
xlabel('time t in secs')
ylabel('EOG signal amplitude')
grid on
title('EOG signal emplitude vs time')
meaneog = mean(eog);
poweog = (1/length(eog))*sum((eog - meaneog).^2);
fprintf('Mean value of EOG signal is %.4f V\n',meaneog)
fprintf('Power of the EOG signal is %.4f V^2\n',poweog)
fs = 1/(t(2)-t(1)); % calculating sampling rate
eogdft = fft(eog); N = length(eog); % number of data point in EOG signal
psdeog = (1/(fs*N))*abs(eogdft).^2; % power spectral density of eog signal
At delV =0.2 mL delP = 0.20 mL/sec and Compliance C = 1.00 mL/mmHg
At delV =0.3 mL delP = 0.28 mL/sec and Compliance C = 1.08 mL/mmHg
At delV =0.4 mL delP = 0.35 mL/sec and Compliance C = 1.14 mL/mmHg
Hence, it can be seen that the compliance C is largest when ΔV =0.4 mL.
9.2:
MATLAB code:
load('eog_trimmed.mat');
figure(1)
plot(t,eog)
xlabel('time t in secs')
ylabel('EOG signal amplitude')
grid on
title('EOG signal emplitude vs time')
meaneog = mean(eog);
poweog = (1/length(eog))*sum((eog - meaneog).^2);
fprintf('Mean value of EOG signal is %.4f V\n',meaneog)
fprintf('Power of the EOG signal is %.4f V^2\n',poweog)
fs = 1/(t(2)-t(1)); % calculating sampling rate
eogdft = fft(eog); N = length(eog); % number of data point in EOG signal
psdeog = (1/(fs*N))*abs(eogdft).^2; % power spectral density of eog signal
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

10MATLAB Homework
freq = 0:(fs/N):fs;freq = freq(1:length(freq)-1); % frequency range
figure(2)
plot(freq,psdeog)
xlabel('Frequency (Hz)')
ylabel('Power/Frequency (dB/Hz)')
set(gca,'Xlim',[0,1])
grid on
title('Power spectrum of EOG signal')
Outputs:
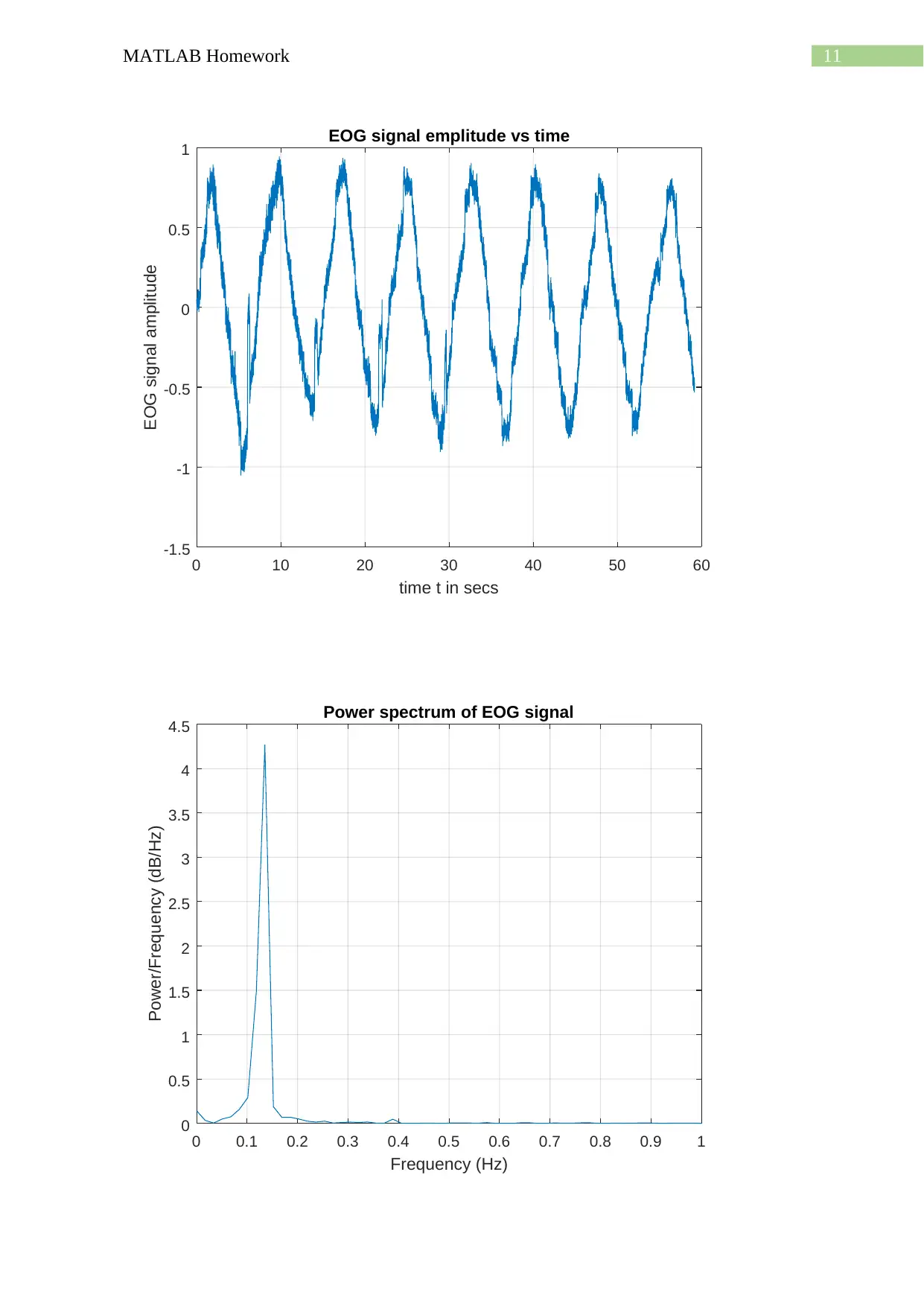
Mean value of EOG signal is 0.0492 V
Power of the EOG signal is 0.2398 V^2
The maximum frequency at which the power spectrum of the EOG reaches its maximum
value is fmax = 0.1352 Hz.
freq = 0:(fs/N):fs;freq = freq(1:length(freq)-1); % frequency range
figure(2)
plot(freq,psdeog)
xlabel('Frequency (Hz)')
ylabel('Power/Frequency (dB/Hz)')
set(gca,'Xlim',[0,1])
grid on
title('Power spectrum of EOG signal')
Outputs:
Mean value of EOG signal is 0.0492 V
Power of the EOG signal is 0.2398 V^2
The maximum frequency at which the power spectrum of the EOG reaches its maximum
value is fmax = 0.1352 Hz.
11MATLAB Homework
0 10 20 30 40 50 60
time t in secs
-1.5
-1
-0.5
0
0.5
1
EOG signal amplitude
EOG signal emplitude vs time
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Frequency (Hz)
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
Power/Frequency (dB/Hz)
Power spectrum of EOG signal
0 10 20 30 40 50 60
time t in secs
-1.5
-1
-0.5
0
0.5
1
EOG signal amplitude
EOG signal emplitude vs time
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Frequency (Hz)
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
Power/Frequency (dB/Hz)
Power spectrum of EOG signal
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 13
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.