Matrices and Interest Rates: Analysis of Financial Problems

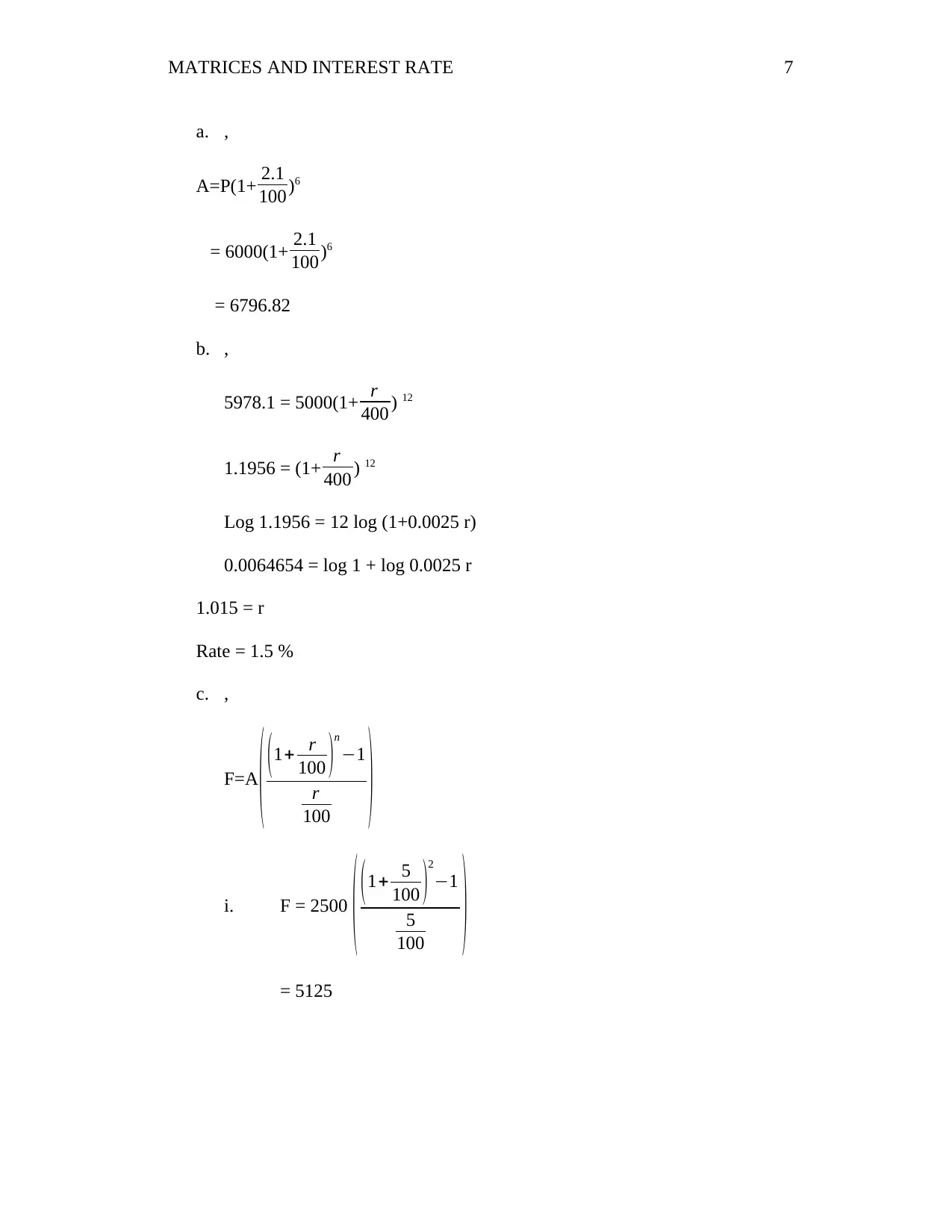
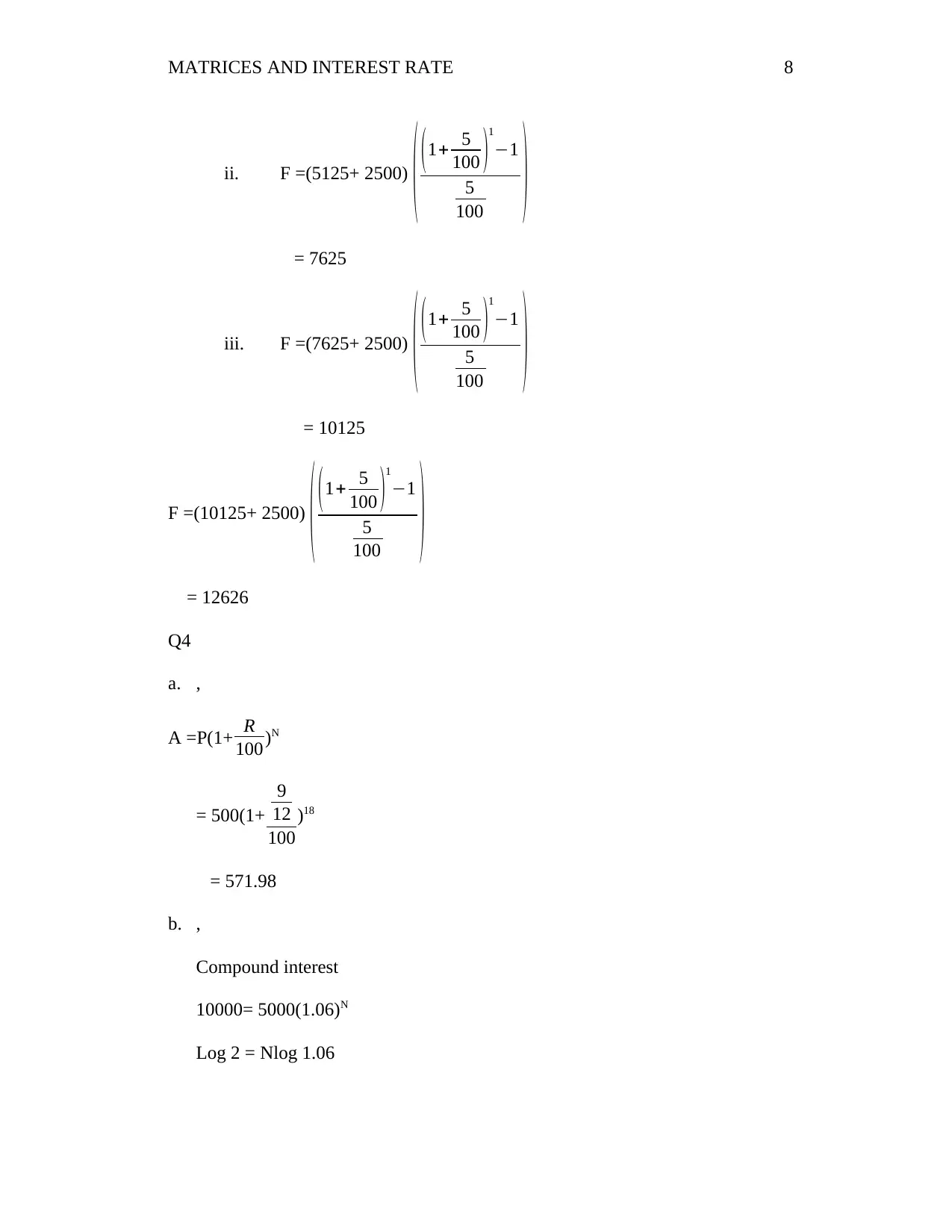
This assignment solution covers various aspects of matrices and interest rates, including matrix operations, solving linear equations using Gaussian elimination and Cramer's rule, and financial calculations such as compound interest. The solution demonstrates the application of matrices in solving financial problems, including calculating future values and determining interest rates. The assignment includes detailed step-by-step solutions for each problem, providing a comprehensive understanding of the concepts and methodologies involved. The solution also provides examples of arithmetic progressions and their applications. This document is a helpful resource for students studying finance and mathematics, providing practical examples of how to solve real-world problems.

Running Head: MATRICES AND INTEREST RATES
MATRICES AND INTEREST RATES
Name
Institute of Affiliation
Date

MATRICES AND INTEREST RATE 2
Question 1
i. ,
A=
[1 0
3 −5 ] , B= [−2 1
4 −3 ]
A +B = [ −2 1
4 −3 ] + [ 1 0
3 −5 ]
= [−1 1
7 −8 ]
ii. ,
2A - 3B =2 [ −2 1
4 −3 ] -3 [ 1 0
3 −5 ]
= [−4 2
8 −6 ] - [−3 0
−9 −15 ]
= [ −1 2
17 9 ]
iii. ,
AB= [−2 1
4 −3 ] . [1 0
3 −5 ]
= [ −2 1
−26 18 ]
iv. ,
AB+BA = [−2 1
4 −3 ] . [1 0
3 −5 ] +. [1 0
3 −5 ] .[−2 1
4 −3 ]
= [ −1 −4
−31 33 ]
b. ,
A= [ 3 2
−1 1 ]

MATRICES AND INTEREST RATE 3
B= [ 0 4
−2 8 ]
X=2A -B
= 2 [ 3 2
−1 1 ] - [ 0 4
−2 8 ]
= [ −2 1
−56 39 ]
c. ,
i.
A= [ 3 2
1 6 ]
Det A= (3 x 6) – (1 x 2)
=16
ii.
A−1 = 1
16 [ 6 −2
−1 3 ]
= [ 0.3750 −0.1250
−0.0625 0.1875 ]
iii. ,
AX=[ 5 6
7 2 ]
X= A−1
[ 5 6
7 2 ]
= [ 0.3750 −0.1250
−0.0625 0.1875 ]. [5 6
7 2 ]
= 1.5000 0.5000
2.5000 0.5000

MATRICES AND INTEREST RATE 4
v. ,
YA=[ 5 6
7 2 ]
Y= A−1
[ 5 6
7 2 ]
= 0 1
0 .5000 −0.5000
Question 2
a. ,
X+3y = -10
3x+2y = 5
.x = -3y-10
3(-3y-10) + 2y = 5
-9y -30 + 2y = 5
-7y = 35
Y=-5
X= -3(-5) -10
= 5
b. ,
3x +2y = 9
4x -3y=12
12x + 8y = 36
12x -9y = 36
17y =0
Y=0

MATRICES AND INTEREST RATE 5
3x +0 = 9
X=3
c. ,
x1−4 x2 + x3=0
2 x1 −3 x2 +7 x3=0
x1−2 x2 =0
[1 −4 1
2 −3 7
1 −2 0 ] { x1
x2
x3
} = {
0
0
0 }
Gaussian elimination
[1 −4 1 ¿ 0
2 −3 7 ¿ 0
1 −2 0 ¿ 0 ]
d. 2x+y = 5
x-y= 1
[2 1
1 −1 ] { x
y } = [5
1 ]
Det a = (-1*2)-(1*1)
= -3
Inv a = 1
−3 [ −1 −1
−1 2 ]
= [ 0.3750 −0.1250
−0.0625 0.1875 ]
{ x
y }=¿ [ 0.3750 −0.1250
−0.0625 0.1875 ][ 5
1 ]
= [ 2
1 ]

MATRICES AND INTEREST RATE 6
e. ,
f. 2x+y = 5
x-y= 1
[ 2 1
1 −1 ] { x
y } = [ 5
1 ]
Augmented matrix is as follows
[ 2 1 ¿5
1 −1 ¿ 1 ]
g. , crammers rule
For y y= [ 2 5
1 1 ]
Det y = ( 2∗1 )−(5∗1)
= -3
For x [5 1
1 −1 ]
Det x = 5*-1 – 1*1
= -6
X= detx/det
= -6/-2
= 2
Y= dety/det
= -3/-3
= 1
Question 3

MATRICES AND INTEREST RATE 7
a. ,
A=P(1+ 2.1
100)6
= 6000(1+ 2.1
100)6
= 6796.82
b. ,
5978.1 = 5000(1+ r
400 ) 12
1.1956 = (1+ r
400 ) 12
Log 1.1956 = 12 log (1+0.0025 r)
0.0064654 = log 1 + log 0.0025 r
1.015 = r
Rate = 1.5 %
c. ,
F=A
( (1+ r
100 )n
−1
r
100 )
i. F = 2500
( (1+ 5
100 )2
−1
5
100 )
= 5125

MATRICES AND INTEREST RATE 8
ii. F =(5125+ 2500)
( (1+ 5
100 )1
−1
5
100 )
= 7625
iii. F =(7625+ 2500)
( (1+ 5
100 )1
−1
5
100 )
= 10125
F =(10125+ 2500)
( (1+ 5
100 )1
−1
5
100 )
= 12626
Q4
a. ,
A =P(1+ R
100)N
= 500(1+
9
12
100
)18
= 571.98
b. ,
Compound interest
10000= 5000(1.06)N
Log 2 = Nlog 1.06

MATRICES AND INTEREST RATE 9
N= log 2
log 1.06
= 11.89 years
c. ,
i. ,
a= 5
ii. ,
d= 11-5 = 17-11
= 6
iii. ,
The 15th term = a + d(15-1)
= 5 + ( 6 *14)
= 89