LB5230 - Strategic Resource Management for Casino Revenue Growth
VerifiedAdded on 2023/06/03
|7
|1576
|125
Report
AI Summary
This report focuses on maximizing the revenue of a casino recently acquired by Holiday Entertainment Corporation (HEC) through strategic decision-making. Three different strategies are evaluated using linear programming in Excel Solver: a base model, an alternative 1 model, and an alternative 2 model. The base model establishes a baseline with given revenue, expenses, and space constraints, determining the optimal number of pokies, gamers, show guests, and high rollers. Alternative 1 explores reducing the buffet dining area and removing limits on gamers and high rollers while maintaining or exceeding the base model's revenue. Alternative 2 investigates mixed guest types to maximize income, compromising dining areas for more space and setting a minimum income target. The analysis reveals that Alternative 2 yields the highest revenue, making it the recommended strategy for HEC to implement in their casino.

INDIVIDUAL TASK COVER SHEET
Student
Please sign, date and attach cover sheet to front of written assessment task OR
Submit as a separate document for non-written assessment task.
A cover sheet is to be completed for each assessment task.
SUBJECT CODE LB5230
STUDENT FAMILY NAME Student Given Name JCU Student Number
Kalra Chirag 1 3 3 0 7 3 9 6
ASSESSMENT TITLE Managing Strategic Resources and Operations
DUE DATE 27-04-2018
LECTURER NAME Dr. Max Boudan
TUTOR NAME Dwight K.Lemke
Student Declaration
1. This assignment is my original work and no part has been copied/ reproduced from any other person’s work or from
any other source, except where acknowledgement has been made (see Learning, Teaching and Assessment Policy
5.1).
2. This work has not been submitted for any other course/subject (see Learning, Teaching and Assessment Policy 5.9).
3. This assignment has not been written for me by anyone or by any organisation.
4. I hold a copy of this assignment and can produce a copy if requested.
5. This work may be used for the purposes of moderation and identifying plagiarism.
6. I give permission for a copy of this marked assignment to be retained by the College for benchmarking and course
review and accreditation purposes.
Learning, Teaching and Assessment Policy 5.1. A student who submits work containing plagiarised material for assessment
will be subject to the provisions of the Student Academic Misconduct Requirements.
Note definition of plagiarism and self-plagiarism in Learning, Teaching and Assessment Policy:
Plagiarism: reproduction without acknowledgement of another person’s words, work or expressed thoughts from any source.
The definition of words, works and thoughts includes such representations as diagrams, drawings, sketches, pictures, objects,
text, lecture hand-outs, artistic works and other such expressions of ideas, but hereafter the term ‘work’ is used to embrace all
of these. Plagiarism comprises not only direct copying of aspects of another person’s work but also the reproduction, even if
slightly rewritten or adapted, of someone else’s ideas. In both cases, someone else’s work is presented as the student’s own.
Under the Australian Copyright Act 1968 a copyright owner can take legal action in the courts against a party who has infringed
their copyright.
Self-Plagiarism: the use of one’s own previously assessed material being resubmitted without acknowledgement or citing of
the original.
Student Signature
Chirag Kalra Submission date 27 / 04 / 2018
ASSESSMENT TASK No _1A______________
Student
Please sign, date and attach cover sheet to front of written assessment task OR
Submit as a separate document for non-written assessment task.
A cover sheet is to be completed for each assessment task.
SUBJECT CODE LB5230
STUDENT FAMILY NAME Student Given Name JCU Student Number
Kalra Chirag 1 3 3 0 7 3 9 6
ASSESSMENT TITLE Managing Strategic Resources and Operations
DUE DATE 27-04-2018
LECTURER NAME Dr. Max Boudan
TUTOR NAME Dwight K.Lemke
Student Declaration
1. This assignment is my original work and no part has been copied/ reproduced from any other person’s work or from
any other source, except where acknowledgement has been made (see Learning, Teaching and Assessment Policy
5.1).
2. This work has not been submitted for any other course/subject (see Learning, Teaching and Assessment Policy 5.9).
3. This assignment has not been written for me by anyone or by any organisation.
4. I hold a copy of this assignment and can produce a copy if requested.
5. This work may be used for the purposes of moderation and identifying plagiarism.
6. I give permission for a copy of this marked assignment to be retained by the College for benchmarking and course
review and accreditation purposes.
Learning, Teaching and Assessment Policy 5.1. A student who submits work containing plagiarised material for assessment
will be subject to the provisions of the Student Academic Misconduct Requirements.
Note definition of plagiarism and self-plagiarism in Learning, Teaching and Assessment Policy:
Plagiarism: reproduction without acknowledgement of another person’s words, work or expressed thoughts from any source.
The definition of words, works and thoughts includes such representations as diagrams, drawings, sketches, pictures, objects,
text, lecture hand-outs, artistic works and other such expressions of ideas, but hereafter the term ‘work’ is used to embrace all
of these. Plagiarism comprises not only direct copying of aspects of another person’s work but also the reproduction, even if
slightly rewritten or adapted, of someone else’s ideas. In both cases, someone else’s work is presented as the student’s own.
Under the Australian Copyright Act 1968 a copyright owner can take legal action in the courts against a party who has infringed
their copyright.
Self-Plagiarism: the use of one’s own previously assessed material being resubmitted without acknowledgement or citing of
the original.
Student Signature
Chirag Kalra Submission date 27 / 04 / 2018
ASSESSMENT TASK No _1A______________
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Table of Contents
Introduction:...............................................................................................................................................3
Base model:................................................................................................................................................3
Alternative 1 model:...................................................................................................................................4
Alternative 2 model:...................................................................................................................................6
Conclusion:................................................................................................................................................7
Introduction:...............................................................................................................................................3
Base model:................................................................................................................................................3
Alternative 1 model:...................................................................................................................................4
Alternative 2 model:...................................................................................................................................6
Conclusion:................................................................................................................................................7
Introduction:
In this assignment the main objective is to maximize the revenue of the casino recently owned
by Holiday Entertainment Corporation (HEC) by choosing a specific strategy. Hence, a total of 3
strategies are evaluated by the method of optimization by using Linear Programming in excel solver
and then the best strategy is chosen. The three models that are evaluated are base model, alternative 1
and alternative 2 model. In all the models the optimum number of pokies, gamers, show guests and
high rollers that will generate the maximum income are calculated with some constraints as specified
below.
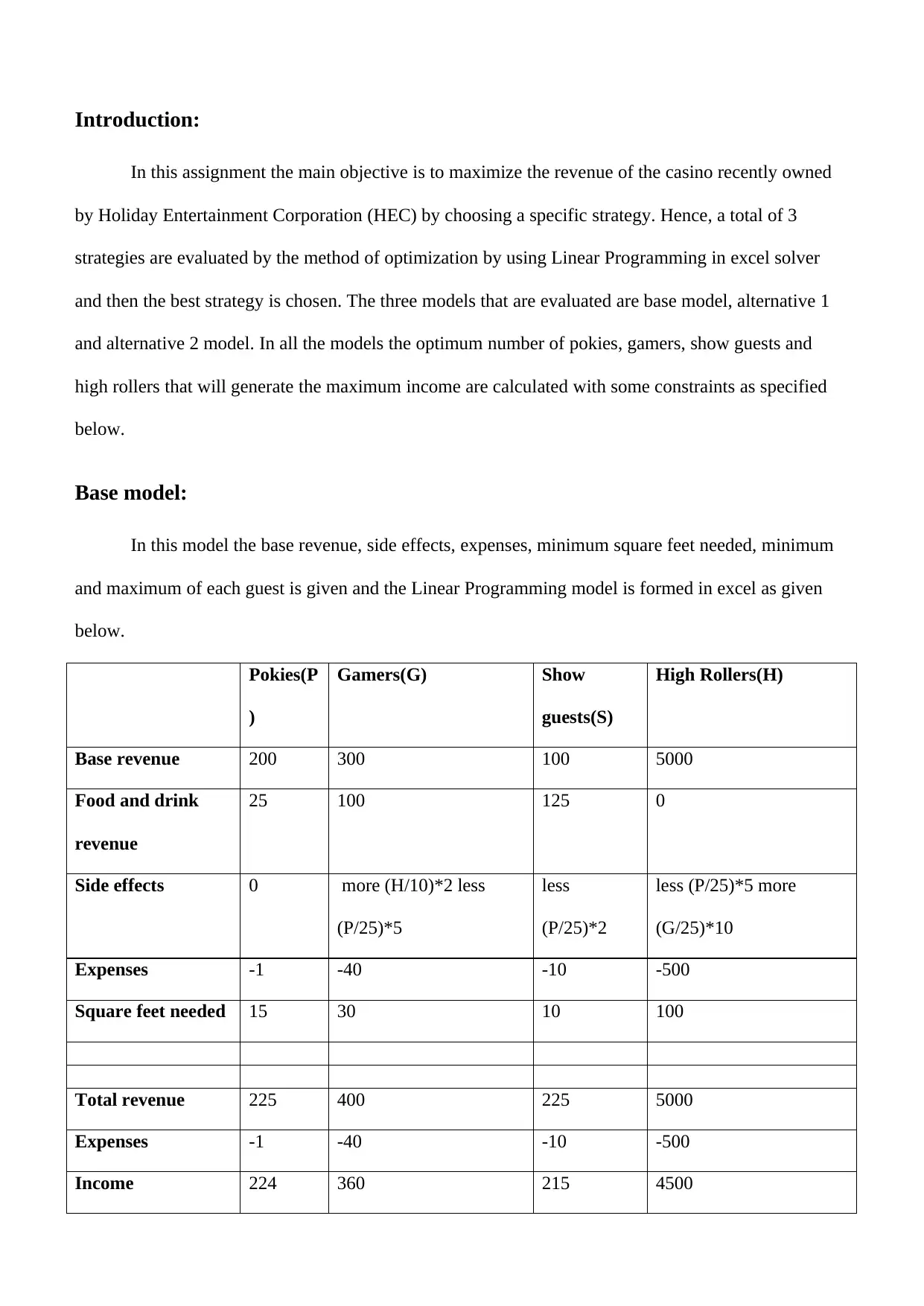
Base model:
In this model the base revenue, side effects, expenses, minimum square feet needed, minimum
and maximum of each guest is given and the Linear Programming model is formed in excel as given
below.
Pokies(P
)
Gamers(G) Show
guests(S)
High Rollers(H)
Base revenue 200 300 100 5000
Food and drink
revenue
25 100 125 0
Side effects 0 more (H/10)*2 less
(P/25)*5
less
(P/25)*2
less (P/25)*5 more
(G/25)*10
Expenses -1 -40 -10 -500
Square feet needed 15 30 10 100
Total revenue 225 400 225 5000
Expenses -1 -40 -10 -500
Income 224 360 215 4500
In this assignment the main objective is to maximize the revenue of the casino recently owned
by Holiday Entertainment Corporation (HEC) by choosing a specific strategy. Hence, a total of 3
strategies are evaluated by the method of optimization by using Linear Programming in excel solver
and then the best strategy is chosen. The three models that are evaluated are base model, alternative 1
and alternative 2 model. In all the models the optimum number of pokies, gamers, show guests and
high rollers that will generate the maximum income are calculated with some constraints as specified
below.
Base model:
In this model the base revenue, side effects, expenses, minimum square feet needed, minimum
and maximum of each guest is given and the Linear Programming model is formed in excel as given
below.
Pokies(P
)
Gamers(G) Show
guests(S)
High Rollers(H)
Base revenue 200 300 100 5000
Food and drink
revenue
25 100 125 0
Side effects 0 more (H/10)*2 less
(P/25)*5
less
(P/25)*2
less (P/25)*5 more
(G/25)*10
Expenses -1 -40 -10 -500
Square feet needed 15 30 10 100
Total revenue 225 400 225 5000
Expenses -1 -40 -10 -500
Income 224 360 215 4500
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Objective Function 224*P + 360*G + 215*S + 4500*H + H/5 - P/5 - 2*P/25 - P/5 + 2*G/5
MAXIMIZE 5588*P/25 + 1802*G/5 + 215*S + 22501*H/5
Constraints
P*15 + G*30 + S*10 + H*100 <= (50000- 5000 -5000)
P + G + S + H <= 1850
Additional
constraints
600 <= P <= 800
400 <= G <= 800
300 <= S <= 800
20 <= H <= 60
The optimum number of guests satisfying all the constraints are
Pokies = 600, Guests = 655, Show guests = 535 and High rollers = 60
And the maximized revenue is $755211.
Alternative 1 model:
In this model the conditions of base model is considered along with the condition that the buffet
dining area can be reduced from 5000 square feet to 1500 square feet and the maximum number of
gamers and high rollers can be removed such that the revenue generated is not less than the same in
base model. The LP which is formulated in excel solver is given below.
Pokies(P
)
Gamers(G) Show
guests(S)
High Rollers(H)
Base revenue 200 300 100 5000
Food and drink 25 100 125 0
MAXIMIZE 5588*P/25 + 1802*G/5 + 215*S + 22501*H/5
Constraints
P*15 + G*30 + S*10 + H*100 <= (50000- 5000 -5000)
P + G + S + H <= 1850
Additional
constraints
600 <= P <= 800
400 <= G <= 800
300 <= S <= 800
20 <= H <= 60
The optimum number of guests satisfying all the constraints are
Pokies = 600, Guests = 655, Show guests = 535 and High rollers = 60
And the maximized revenue is $755211.
Alternative 1 model:
In this model the conditions of base model is considered along with the condition that the buffet
dining area can be reduced from 5000 square feet to 1500 square feet and the maximum number of
gamers and high rollers can be removed such that the revenue generated is not less than the same in
base model. The LP which is formulated in excel solver is given below.
Pokies(P
)
Gamers(G) Show
guests(S)
High Rollers(H)
Base revenue 200 300 100 5000
Food and drink 25 100 125 0
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
revenue
Side effects 0 more (H/10)*2 less
(P/25)*5
less
(P/25)*2
less (P/25)*5 more
(G/25)*10
Expenses -1 -40 -10 -500
Square feet needed 15 30 10 100
Total revenue 225 400 225 5000
Expenses -1 -40 -10 -500
Income 224 360 215 4500
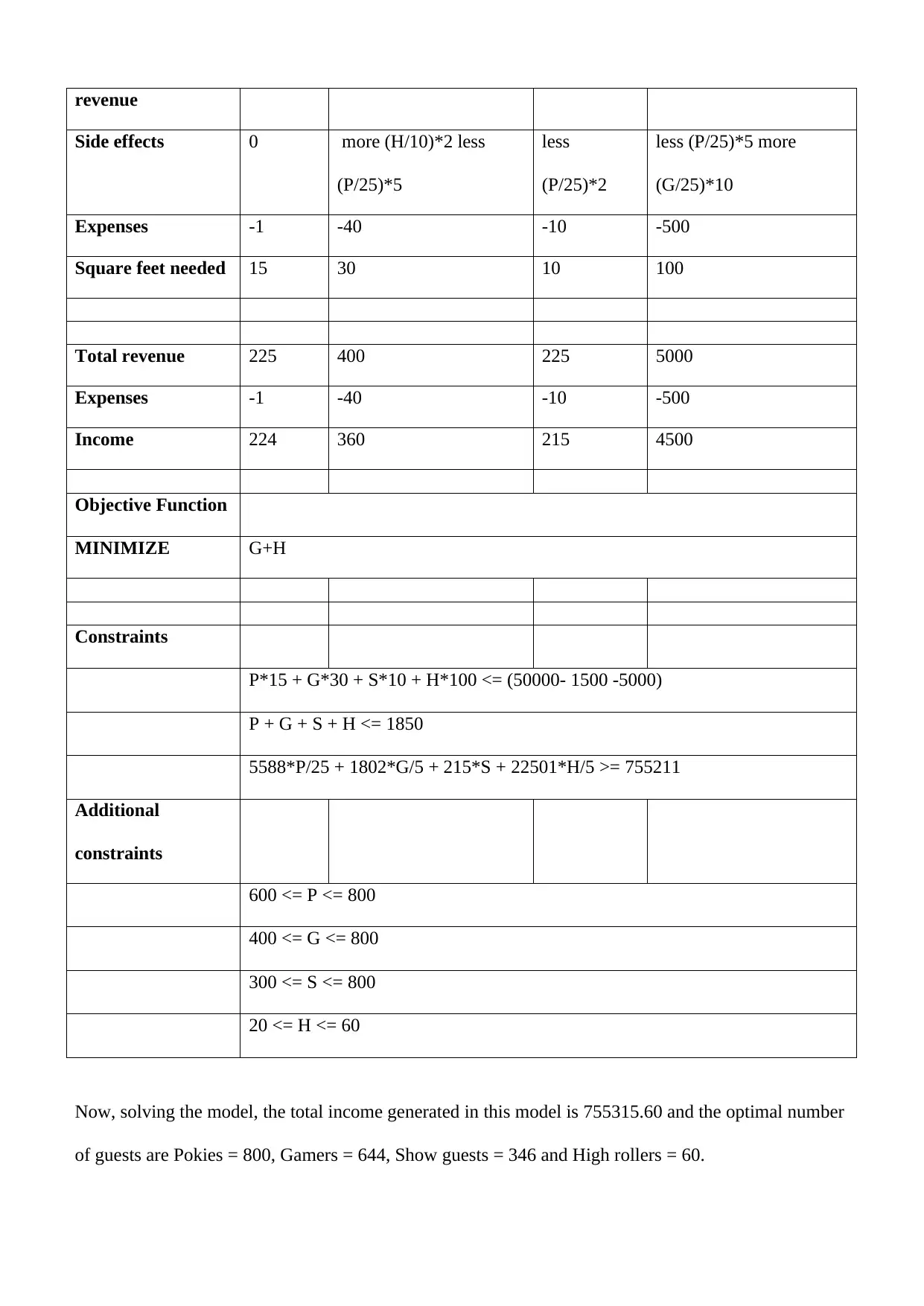
Objective Function
MINIMIZE G+H
Constraints
P*15 + G*30 + S*10 + H*100 <= (50000- 1500 -5000)
P + G + S + H <= 1850
5588*P/25 + 1802*G/5 + 215*S + 22501*H/5 >= 755211
Additional
constraints
600 <= P <= 800
400 <= G <= 800
300 <= S <= 800
20 <= H <= 60
Now, solving the model, the total income generated in this model is 755315.60 and the optimal number
of guests are Pokies = 800, Gamers = 644, Show guests = 346 and High rollers = 60.
Side effects 0 more (H/10)*2 less
(P/25)*5
less
(P/25)*2
less (P/25)*5 more
(G/25)*10
Expenses -1 -40 -10 -500
Square feet needed 15 30 10 100
Total revenue 225 400 225 5000
Expenses -1 -40 -10 -500
Income 224 360 215 4500
Objective Function
MINIMIZE G+H
Constraints
P*15 + G*30 + S*10 + H*100 <= (50000- 1500 -5000)
P + G + S + H <= 1850
5588*P/25 + 1802*G/5 + 215*S + 22501*H/5 >= 755211
Additional
constraints
600 <= P <= 800
400 <= G <= 800
300 <= S <= 800
20 <= H <= 60
Now, solving the model, the total income generated in this model is 755315.60 and the optimal number
of guests are Pokies = 800, Gamers = 644, Show guests = 346 and High rollers = 60.
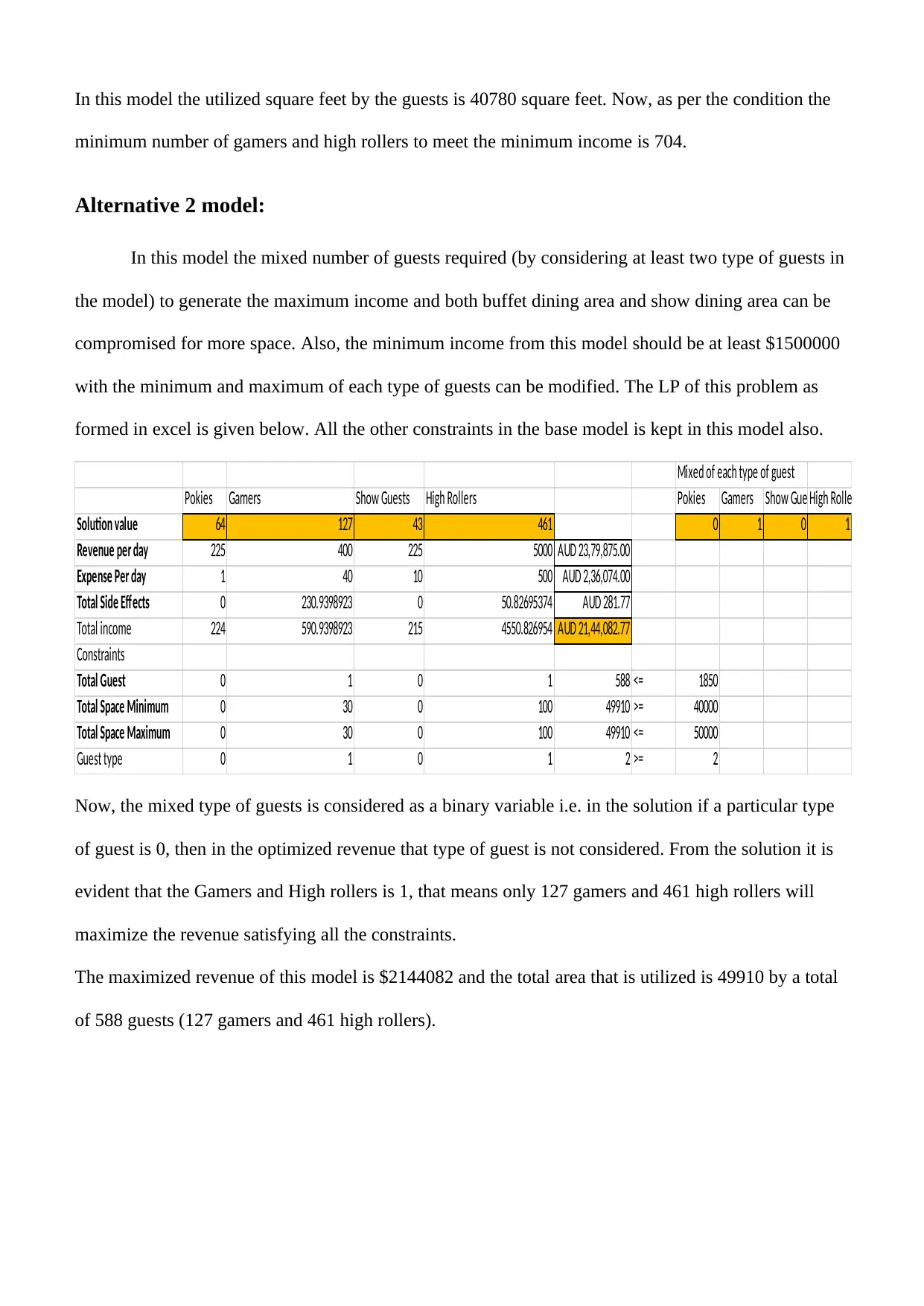
In this model the utilized square feet by the guests is 40780 square feet. Now, as per the condition the
minimum number of gamers and high rollers to meet the minimum income is 704.
Alternative 2 model:
In this model the mixed number of guests required (by considering at least two type of guests in
the model) to generate the maximum income and both buffet dining area and show dining area can be
compromised for more space. Also, the minimum income from this model should be at least $1500000
with the minimum and maximum of each type of guests can be modified. The LP of this problem as
formed in excel is given below. All the other constraints in the base model is kept in this model also.
Mixed of each type of guest
Pokies Gamers Show Guests High Rollers Pokies Gamers Show GuestsHigh Rollers
Solution value 64 127 43 461 0 1 0 1
Revenue per day 225 400 225 5000 AUD 23,79,875.00
Expense Per day 1 40 10 500 AUD 2,36,074.00
Total Side Effects 0 230.9398923 0 50.82695374 AUD 281.77
Total income 224 590.9398923 215 4550.826954 AUD 21,44,082.77
Constraints
Total Guest 0 1 0 1 588 <= 1850
Total Space Minimum 0 30 0 100 49910 >= 40000
Total Space Maximum 0 30 0 100 49910 <= 50000
Guest type 0 1 0 1 2 >= 2
Now, the mixed type of guests is considered as a binary variable i.e. in the solution if a particular type
of guest is 0, then in the optimized revenue that type of guest is not considered. From the solution it is
evident that the Gamers and High rollers is 1, that means only 127 gamers and 461 high rollers will
maximize the revenue satisfying all the constraints.
The maximized revenue of this model is $2144082 and the total area that is utilized is 49910 by a total
of 588 guests (127 gamers and 461 high rollers).
minimum number of gamers and high rollers to meet the minimum income is 704.
Alternative 2 model:
In this model the mixed number of guests required (by considering at least two type of guests in
the model) to generate the maximum income and both buffet dining area and show dining area can be
compromised for more space. Also, the minimum income from this model should be at least $1500000
with the minimum and maximum of each type of guests can be modified. The LP of this problem as
formed in excel is given below. All the other constraints in the base model is kept in this model also.
Mixed of each type of guest
Pokies Gamers Show Guests High Rollers Pokies Gamers Show GuestsHigh Rollers
Solution value 64 127 43 461 0 1 0 1
Revenue per day 225 400 225 5000 AUD 23,79,875.00
Expense Per day 1 40 10 500 AUD 2,36,074.00
Total Side Effects 0 230.9398923 0 50.82695374 AUD 281.77
Total income 224 590.9398923 215 4550.826954 AUD 21,44,082.77
Constraints
Total Guest 0 1 0 1 588 <= 1850
Total Space Minimum 0 30 0 100 49910 >= 40000
Total Space Maximum 0 30 0 100 49910 <= 50000
Guest type 0 1 0 1 2 >= 2
Now, the mixed type of guests is considered as a binary variable i.e. in the solution if a particular type
of guest is 0, then in the optimized revenue that type of guest is not considered. From the solution it is
evident that the Gamers and High rollers is 1, that means only 127 gamers and 461 high rollers will
maximize the revenue satisfying all the constraints.
The maximized revenue of this model is $2144082 and the total area that is utilized is 49910 by a total
of 588 guests (127 gamers and 461 high rollers).
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Conclusion:
Now, comparing the three models above namely base model, alternative 1 model and the
alternative 2 model it is seen that the income is maximum in the alternative 2 model and hence the best
strategy for maximizing the income from the casino is to employ the alternative 2 model by Holiday
Entertainment Corporation.
Now, comparing the three models above namely base model, alternative 1 model and the
alternative 2 model it is seen that the income is maximum in the alternative 2 model and hence the best
strategy for maximizing the income from the casino is to employ the alternative 2 model by Holiday
Entertainment Corporation.
1 out of 7
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





