MCE226L, Mini-Project

This document explains the Mittag-Leffler function with parameters α, β and its approximation using C programming. It includes a flowchart and C program for the same.

Running head: MCE226L, Mini-Project
Type equation here .
MCE226L, Mini-Project
Name of the Student
Name of the University
Author Note

1MCE226L, Mini-Project
The Mittag-Leffler function with parameters α, β are given by the following expression.
M L ( α , β ) ( z )=∑
k=0
∞ zk
Γ ( α∗k+ β )
The Γ symbol is the gamma function which is defined by,
Γ ( n)=(n−1)!
The infinite sum of M-L function is approximated by certain number of terms in which the
error between current and next iteration is less than the tolerance which is En =0.0001. The
values of α, β are considered positive integers here. The values of M-L function for different
z in a user-defined range are printed using C programming.
Flowchart of algorithm:

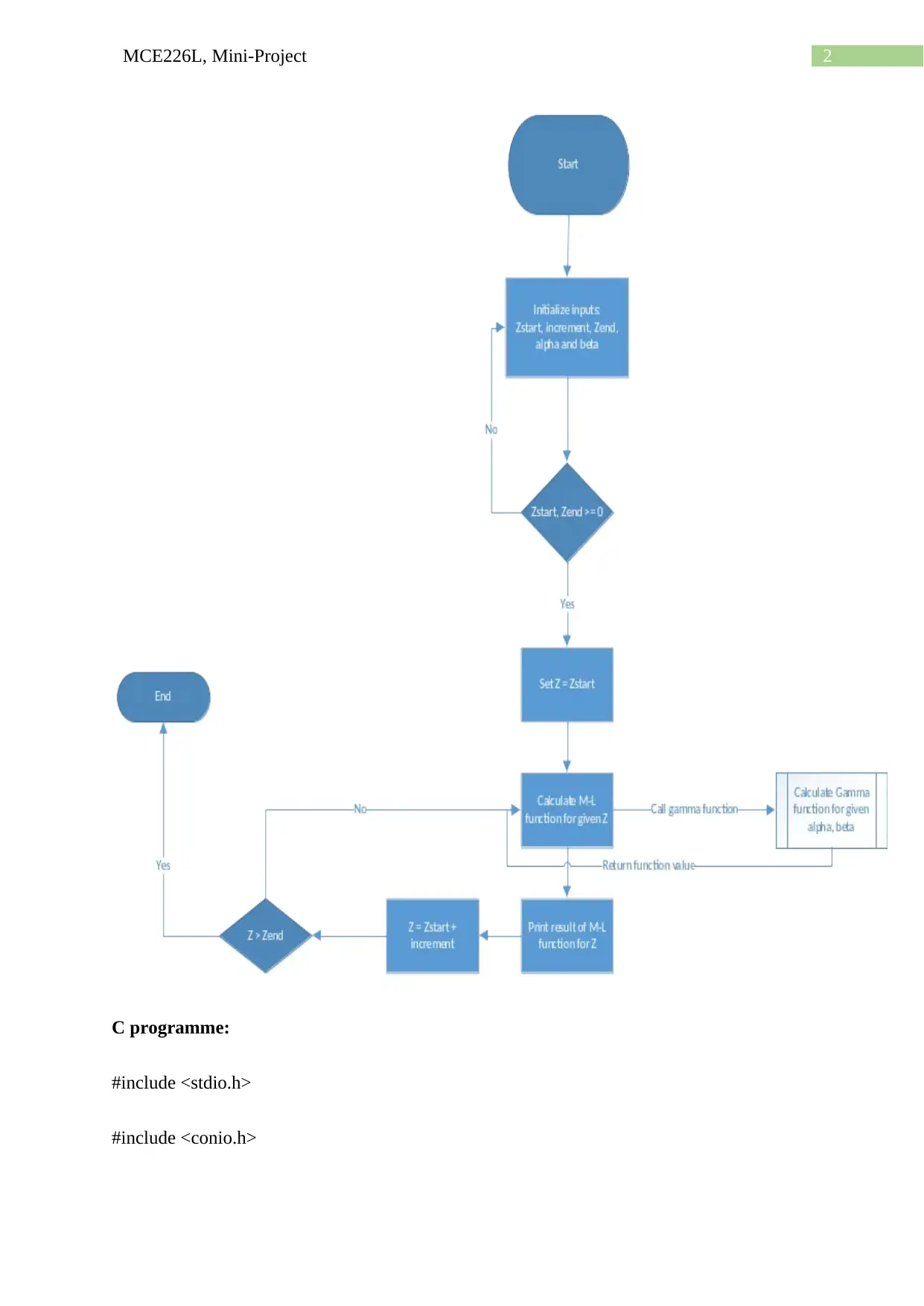
2MCE226L, Mini-Project
C programme:
#include <stdio.h>
#include <conio.h>

3MCE226L, Mini-Project
#include <math.h>
#include <stdlib.h>
int gammafunc(int num);
int main()
{
// initialization of paramters
float zstart;
float zend;
float inc;
float z;
int alpha;
int beta;
printf("Enter positive value of starting z: ");
scanf("%f",&zstart);
while (zstart<0)
{

4MCE226L, Mini-Project
printf("You must enter positive value of starting z: ");
scanf("%f",&zstart);
}
printf("Enter positive value of ending z: ");
scanf("%f",&zend);
while (zend<0)
{
printf("You must enter positive value of ending z: ");
scanf("%f",&zend);
}
printf("Enter positive value of increment: ");
scanf("%f",&inc);
printf("Enter value of alpha which is integer: ");
scanf("%d",&alpha);
printf("Enter value of beta which is integer: ");
scanf("%d",&beta);

5MCE226L, Mini-Project
for (z=zstart;z<zend;z=z+inc)
{
float out1; int k;float out2; k=0;
out1= 0;
out2 = pow(z,k)/gammafunc(alpha*(k) + beta);
// Calculation loop
while (fabs(out2 - out1)>=0.0001) // tolerance is 1e-4
{
out1 = out1 + pow(z,k)/gammafunc(alpha*k + beta);
out2 = out1 + pow(z,k+1)/gammafunc(alpha*(k+1) + beta);
k=k+1;
}
printf("The value of the Mittag-Leffler function for the input %.4f is %.4f \n",z,out2);
}
return 0;
}
int gammafunc(int num) // function definition
{

6MCE226L, Mini-Project
{
int fact=1,i;
for (i=1;i<=num-1;i++)
{
fact = fact*i;
}
return fact;
} // return statement
}
Sample Output:

7MCE226L, Mini-Project