Fatigue Curve Fitting for Steel Material Specimens

This assignment deals with fitting two models to a sample S-N curve data for steel material specimens. The best model is obtained from the plot and numerical results of the model. The predictor has the p value less than 0.05 (significance level) and hence the predictor number of cycles Nf is significant with confidence interval [4.13,5.57].

Running head: MECH2450 ENGINEERING COMPUTATIONS 2
MECH2450 ENGINEERING COMPUTATIONS 2
Name of the Student
Name of the University
Author Note

1MECH2450 ENGINEERING COMPUTATIONS 2
Introduction:
The fatigue characteristics of a material is commonly described by its fatigue limit or
through the failure curves like the S-N curve, Wöhler curve or fatigue curve. The relation
between the amplitude of cyclic stress and the number of cycles needed for the failure. In the
horizontal axis of the S-N curve the number of cycles Nf (either in logarithmic or in linear
scale) is taken and in the vertical axis the maximum stress amplitude is displayed in either
logarithmic or in linear scale. The different S-N curves for different materials are generally
derived from different fatigue tests of the materials. In the different tests a constant amplitude
of cyclic stress is applied to a series of the specimens of the material until breakdown or
failure occurs. In a few cases the test is intentionally stopped after reaching a specific number
of cycles usually considered very large (typically Nf>10^6). Often times the fatigue curves
are given by Kt=1 which is un-notched specimens that describes the fatigue characteristics of
materials. Now, in this assignment a sample S-N data is collected for steel material specimens
from the web and then that data is fitted by two curve fitting methods. One method is a non-
linear regression and the other method is invented by Kim and Zhang for fatigue curve fitting
and two methods are compared by both numerical testing and graphical overview. Also, the
best fitted model for the collected S-N data is concluded based on the results of graphical and
numerical testing which is obtained through MATLAB coding.
Methodology:
Now, the sample collected S-N curve data as total of 14 data points in two columns.
In the first column the number of cycles to failure is given and in the second column the
stress amplitude in kPa is given.
Now, the data is loaded in MATLAB and then the number of cycles Nf is converted to 10
base log scale and then the stress amplitude is expressed as a function of log(Nf) by least

2MECH2450 ENGINEERING COMPUTATIONS 2
square method (Gan et al., 2017). Now, in the Kim and Zhang method the formula for S-N
fatigue curve model is given below.
σ max=σuT ¿ ¿
N0=¿ initial cycle number corresponding to ultimate tensile strength σ uT ~ 0.5.
α , β = model parameters.
σ uTfor steel = 7000000 kPa.
σ max = maximum stress amplitude in kPa
Now, the model parameters are estimated by an approximate model of the above which is
log Δ DfT
Δ N f
≈ log α + β log σmax (1)
where, DfT = 1− σ max
σuT
= fatigue damage at tensile fatigue failure.
Δ operators are difference between ith and i+1th entries.
Now, equation (1) is fitted with least square model from which log α and β are estimated and
the parameters are computed (Burhan & Kim, 2018). Then the two models are fitted with the
given data and the accuracy of fitting is displayed by the outputs of the models.
Additionally, the confidence intervals of the slope coefficients and prediction intervals of the
mean maximum stress amplitude is compared.
Results and Discussion:
The output of the MATLAB script modelfit in which the two models are fitted are shown
below.
Output:

3MECH2450 ENGINEERING COMPUTATIONS 2
logmod =
Linear regression model:
y ~ 1 + x1
Estimated Coefficients:
Estimate SE tStat pValue
___________ __________ _______ __________
(Intercept) 2.5103e+06 4.3667e+05 5.7488 9.1812e-05
x1 -3.7431e+05 88174 -4.2451 0.0011371
Number of observations: 14, Error degrees of freedom: 12
Root Mean Squared Error: 8.1e+05
R-squared: 0.6, Adjusted R-Squared 0.567
F-statistic vs. constant model: 18, p-value = 0.00114

4MECH2450 ENGINEERING COMPUTATIONS 2
The confidence interval of b = -374306.91 for logarithimic least square is [-566420.90,-
182192.91]
The prediction interval of mean maximum stress amplitude = 900700.00 is [-
865025.76,2666425.76]
KZmodel =
Linear regression model:
y ~ 1 + x1
Estimated Coefficients:
Estimate SE tStat pValue
________ _______ _______ __________
(Intercept) -32.593 1.8253 -17.857 5.217e-10
x1 4.8488 0.32899 14.738 4.7519e-09
Number of observations: 14, Error degrees of freedom: 12
Root Mean Squared Error: 0.811

5MECH2450 ENGINEERING COMPUTATIONS 2
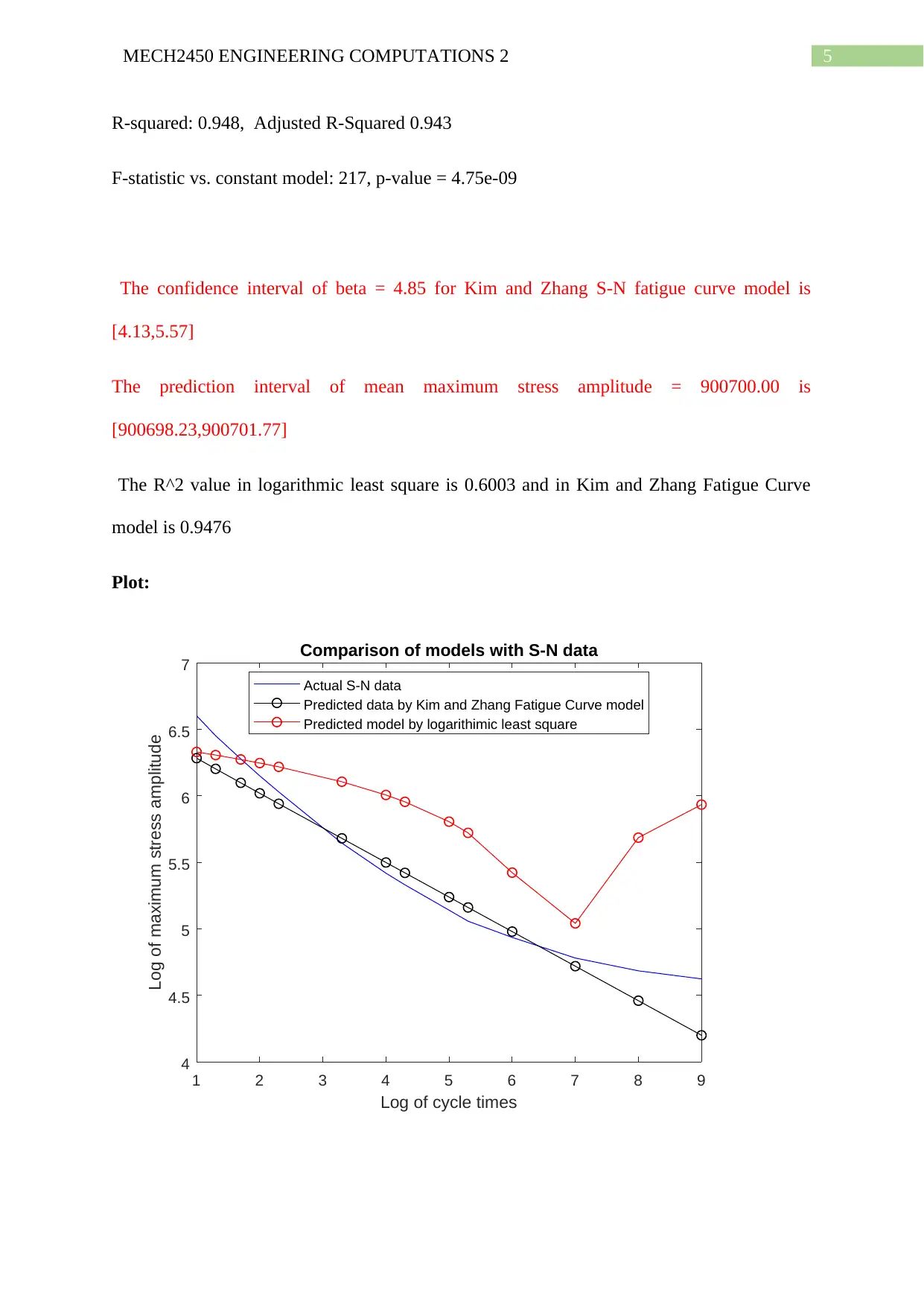
R-squared: 0.948, Adjusted R-Squared 0.943
F-statistic vs. constant model: 217, p-value = 4.75e-09
The confidence interval of beta = 4.85 for Kim and Zhang S-N fatigue curve model is
[4.13,5.57]
The prediction interval of mean maximum stress amplitude = 900700.00 is
[900698.23,900701.77]
The R^2 value in logarithmic least square is 0.6003 and in Kim and Zhang Fatigue Curve
model is 0.9476
Plot:
1 2 3 4 5 6 7 8 9
Log of cycle times
4
4.5
5
5.5
6
6.5
7
Log of maximum stress amplitude
Comparison of models with S-N data
Actual S-N data
Predicted data by Kim and Zhang Fatigue Curve model
Predicted model by logarithimic least square

6MECH2450 ENGINEERING COMPUTATIONS 2
From the above output it can be seen that the Non-linear logarithmic fitted model only
explains 56.7% of the data from the R^2 value and the Kim and Zhang model explains 94.8%
of the variation in dependent maximum stress amplitude by its predictor number of cycles.
This is also evident from the plot that the Kim and Zhang model fitted data is close to the
original S-N data. Hence, the best model which explains the sample S-N data is the Kim and
Zhang model. The predictor has the p value less than 0.05 (significance level) and hence the
predictor number of cycles Nf is significant with confidence interval [4.13,5.57]. Also, the
mean stress amplitude = 900700.00 Kpa has the prediction interval by K-Z method is
[900698.23,900701.77] which is very small and thus K-Z model is an appropriate fit.
Conclusion:
In conclusion it can be stated that the objective of the assignment which is fitting two
models to a sample S-N curve data has been successfully completed and the best model is
obtained from the plot and numerical results of the model. It can also be noted that the Kim
and Zhang model is not an absolute fit to the data as at N0 the maximum applied stress is not
equal to the ultimate tensile stress of steel.

7MECH2450 ENGINEERING COMPUTATIONS 2
References:
Burhan, I., & Kim, H. (2018). SN Curve Models for Composite Materials Characterisation:
An Evaluative Review. Journal of Composites Science, 2(3), 38.
Gan, M., Chen, C. P., Chen, G. Y., & Chen, L. (2017). On some separated algorithms for
separable nonlinear least squares problems. IEEE transactions on cybernetics, 48(10),
2866-2874.

8MECH2450 ENGINEERING COMPUTATIONS 2
Appendix:
MATLAB code:
sndata = readtable('SNdata.xlsx','ReadVariableNames',1);
%% Logarithimic least square fit
Nf = log10([sndata{:,1}]); sigmamax = [sndata{:,2}];
logmod = fitlm(Nf,sigmamax)
coeff = logmod.Coefficients.Estimate; a = coeff(1); b = coeff(2);
sigmamaxpredlin = abs(a + b.*Nf);
cilogmod = coefCI(logmod);
tcrit = abs(tinv(0.05/2,length(Nf)-2));
fprintf('\n The confidence interval of b = %.2f for logarithimic least square is [%.2f,%.2f]\
n',b,cilogmod(2,1),cilogmod(2,2))
ypredlow = mean(sigmamax) - tcrit*sqrt(logmod.MSE); ypredhigh = mean(sigmamax) +
tcrit*sqrt(logmod.MSE); % prediction interval = ybar +/- tcrit*sqrt(MSE)
fprintf('The prediction interval of mean maximum stress amplitude = %.2f is [%.2f,
%.2f]',mean(sigmamax),ypredlow,ypredhigh)
%% Kim and Zhang S-N fatigue curve model fitting
sigmauT = 7000000; % ultimate tensile strength of steel in kPa
N0 = 0.5; % initial number of cylces is approximately 0.5

9MECH2450 ENGINEERING COMPUTATIONS 2
Nf = [N0;sndata{:,1}]; sigmamax = [sigmauT;sndata{:,2}];
Dft = 1 - sigmamax./sigmauT;
for i=1:length(Dft)-1
delDft(i) = Dft(i+1) - Dft(i);
delNf(i) = Nf(i+1)-Nf(i);
ydata(i) = log10(delDft(i)/delNf(i));
end
xdata = log10(sigmamax(2:end));
ydata = ydata';
KZmodel = fitlm(xdata,ydata)
coeff = KZmodel.Coefficients.Estimate;
alpha = 10^(coeff(1)); beta = coeff(2);
Nf = sndata{:,1}; sigmamax = sndata{:,2};
sigmamaxpredKZ = sigmauT.*(alpha*(beta-1).*(Nf-N0)./((sigmauT)^(-beta)) + 1).^(1/(1-
beta));

10MECH2450 ENGINEERING COMPUTATIONS 2
ciKZmod = coefCI(KZmodel);
fprintf('\n The confidence interval of beta = %.2f for Kim and Zhang S-N fatigue curve
model is [%.2f,%.2f] \n',beta,ciKZmod(2,1),ciKZmod(2,2))
ypredlow = mean(sigmamax) - tcrit*sqrt(KZmodel.MSE); ypredhigh = mean(sigmamax) +
tcrit*sqrt(KZmodel.MSE); % prediction interval = ybar +/- tcrit*sqrt(MSE)
fprintf('The prediction interval of mean maximum stress amplitude = %.2f is [%.2f,
%.2f]',mean(sigmamax),ypredlow,ypredhigh)
%% Models comparison with real S-N data
plot(log10(Nf),log10(sigmamax),'b-',log10(Nf),log10(sigmamaxpredKZ),'ko-',log10(Nf),log1
0(sigmamaxpredlin),'ro-')
legend('Actual S-N data','Predicted data by Kim and Zhang Fatigue Curve model','Predicted
model by logarithimic least square','Location','best')
xlabel('Log of cycle times')
ylabel('Log of maximum stress amplitude')
title('Comparison of models with S-N data')
fprintf('\n The R^2 value in logarithimic least square is %.4f and in Kim and Zhang Fatigue
Curve model is %.4f \n',logmod.Rsquared.Ordinary,KZmodel.Rsquared.Ordinary)

11MECH2450 ENGINEERING COMPUTATIONS 2