Mechanical Engineering

Mechanical Engineering

Table of Contents
Activity 1:........................................................................................................................................1
Activity 2.........................................................................................................................................7
Activity 3.......................................................................................................................................12
Activity 4.......................................................................................................................................15
Activity 5.......................................................................................................................................16
Activity 6.......................................................................................................................................17
Activity 7.......................................................................................................................................18

Activity 1:
a) Conversion of numbers into binary, hexadecimal, octal and decimal equivalents
(i) 10101101112
Solution:
Binary to decimal:
= 1 x 29 + 0 x 28 + 1 x 27 + 0 x 26 + 1 x 25 + 1 x 24 + 0 x 23 + 1 x 22 + 1x 21 + 1 x 20
= 512 + 0 + 128 + 0 + 32 + 16 + 0 + 4 + 2 + 1
= 69510
Binary to octal:
10101101112 = 25678
Binary to hexadecimal:
So,
10101101112 = 2B78
(ii) 53278
1

Solution:
Octal to decimal:
= 5 x 83 + 3 x 82 + 2 x 81 + 7 x 80
= 5 x 512 + 3 x 64 + 2 x 16 + 7 x 1
= 279110
Octal to binary
53278 = 1010110101112
Octal to hexadecimal
53278 = 1010110101112
0111 = 7
1101 = D
1010 = A
So, 53278 = 7DA16
(iii) 429A16
Solution: A = 10
Hexadecimal to Octal:
429A16 =
4 – 0100
2 – 0010
9 – 1001
A – 1010
So, 100001010011010
Now, regrouping them –
100 – 4
001 – 1
010 – 2
011 – 3
010 – 2
So, 429A16 = 412328
Hexadecimal to Binary:
2

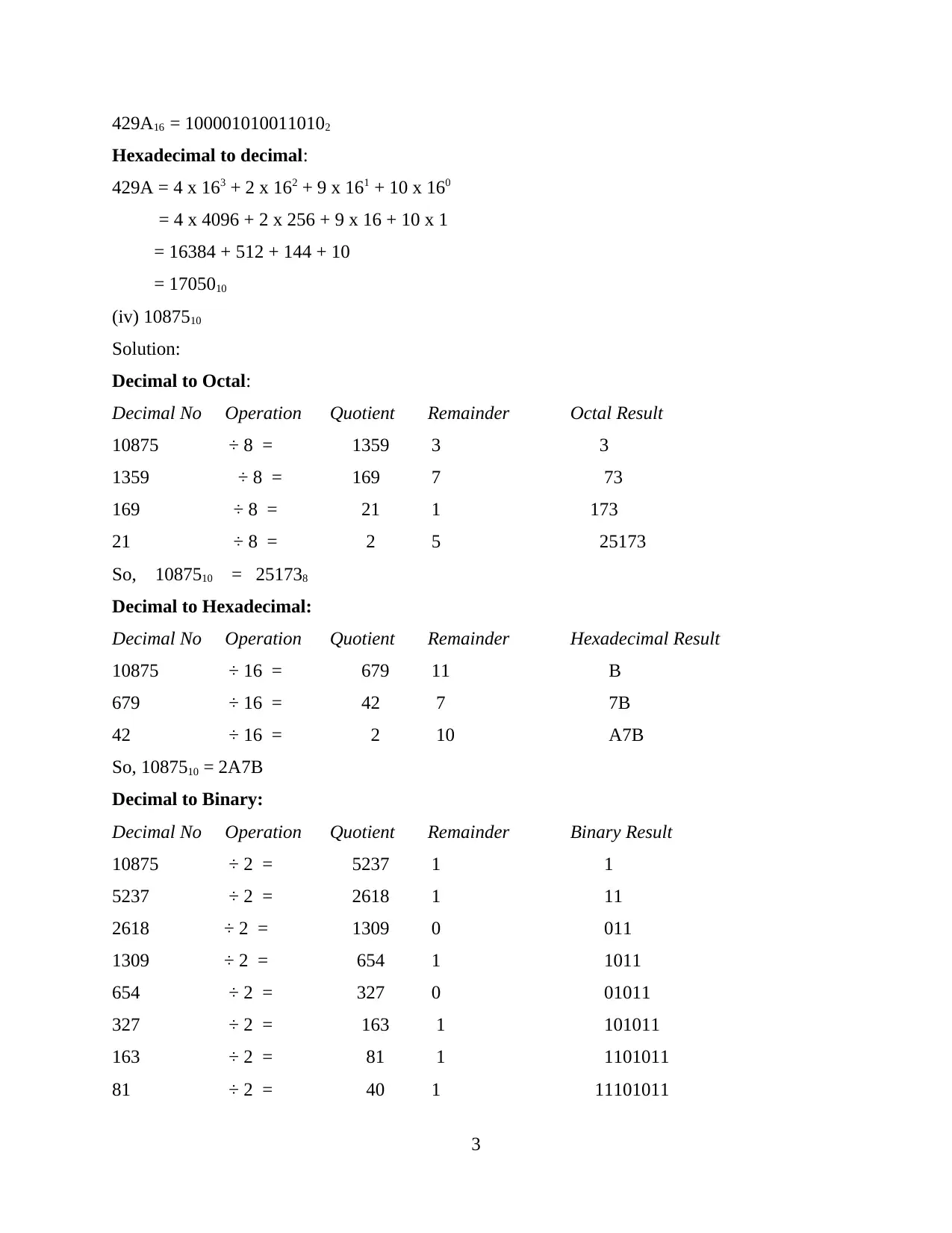
429A16 = 1000010100110102
Hexadecimal to decimal:
429A = 4 x 163 + 2 x 162 + 9 x 161 + 10 x 160
= 4 x 4096 + 2 x 256 + 9 x 16 + 10 x 1
= 16384 + 512 + 144 + 10
= 1705010
(iv) 1087510
Solution:
Decimal to Octal:
Decimal No Operation Quotient Remainder Octal Result
10875 ÷ 8 = 1359 3 3
1359 ÷ 8 = 169 7 73
169 ÷ 8 = 21 1 173
21 ÷ 8 = 2 5 25173
So, 1087510 = 251738
Decimal to Hexadecimal:
Decimal No Operation Quotient Remainder Hexadecimal Result
10875 ÷ 16 = 679 11 B
679 ÷ 16 = 42 7 7B
42 ÷ 16 = 2 10 A7B
So, 1087510 = 2A7B
Decimal to Binary:
Decimal No Operation Quotient Remainder Binary Result
10875 ÷ 2 = 5237 1 1
5237 ÷ 2 = 2618 1 11
2618 ÷ 2 = 1309 0 011
1309 ÷ 2 = 654 1 1011
654 ÷ 2 = 327 0 01011
327 ÷ 2 = 163 1 101011
163 ÷ 2 = 81 1 1101011
81 ÷ 2 = 40 1 11101011
3

40 ÷ 2 = 20 0 011101011
20 ÷ 2 = 10 0 0011101011
10 ÷ 2 = 5 0 00011101011
5 ÷ 2 = 2 1 101001111011
2 ÷ 2 = 1 0 10101001111011
So,
1087510 = 101010011110112
b) Add and multiple the following numbers
(i) 101110012 and 111010102
Solution:
Addition rules –
0 + 0 = 0
0 + 1 = 1 + 0 = 1
1 + 1 = 10
10111001
+ 11101010
110100011
Multiplication rules –
0 x 0 = 0
0 x 1 = 1 x 0 = 0
1 x 1 = 1
So, 10111001
x 11101010
1010100100011010
(ii) 21378 and 15418
Solution: Firstly, convert the numbers from octal into binary form –
21378 = 100010111112
15418 = 11011000012
Addition –
10001011111
+ 01101100001
4

11111000000
So, addition of 21378 and 15418 is 37008 (111110000002)
Similarly, multiplication of 21378 and 15418
10001011111
x 01101100001
11101100010011111111
So, multiplication of 21378 and 15418 is 35423778 (111011000100111111112)
(iii) B41E16 and 253B16
Solution:
Convert the hexadecimal numbers into binary
B41E16 = 1011010000011110
253B16 = 10010100111011
1011010000011110
+ 10010100111011
11000110101011001
So, addition of B41E16 and 253B16 is18D59
Multiplication:
1011010000011110
x 10010100111011
11010001100011101100011101010
So, multiplication of B41E16 and 253B16 is 1A31D8EA16
(iv) 356210 and 264310
Solution:
Convert decimal numbers into binary numbers as –
5

356210 = 1101111010102
264310 = 1010010100112
Addition of both numbers –
110111101010
+ 101001010011
1100000111101
So, addition of 356210 and 264310 is 620510 (11000001111012)
Now, multiplication –
110111101010
x 101001010011
100100110100100000001100
So, multiplication of 356210 and 264310 is 965223610 (11000001111012)
6

Activity 2
(a) Given,
Resistance of resistor R = 12 Ω
Inductance of coil L = 0.1 H
Capacitance C = 150 μF = 150 x 10-6 F
Amplitude of AC Voltage Source Um = 220 V
Resistor, coil and capacitor are connected in series
To determine Phase angle ø?
Current Flowing in the circuit Im ?
Figure 1: Phasor Diagram
(i) Impedance Z can be calculated by taking rectangular triangle as shown in above phasor
diagram in following way –
7

Using Pythagorean Theorem –
Z2 = R2 + (XL – XC)2
Frequency (f) = 1 / 2 √LCℼ
= 41.09
Here, XL = ωL
= 2ℼfL
= 2 x 41.09 x 0.1 = 25.80 Ωℼ
and XC = 1/ ωC
= 1/ 2ℼfC
= 1/ 2ℼ x 41.09 x 150 x 10-6
= 25.84 Ω
So, Impedance in rectangular form –
Z = R + j (XL – XC)
= 12 + j (25.80 – 25.84)
= 12 – j 0.4 Ω
Impedance in polar form –
Z = 12.01 (-1.91 ) Ω⁰
(ii) Impedance at resonance,
At resonance XL = XC
Therefore,
Impedance at resonance in rectangular form
Z = R + j. 0
= 12 Ω
Impedance at resonance in polar form
Z = 12 (0 ) Ω⁰
(iii) Current Flowing in rectangular form –
I = V / Z
= 220 / 12 – j 0.4
In polar form –
8

I = V / Z
= 220 / 12.01 (-1.91 )⁰
(b) Given,
Resistance of resistor R1 = 1k Ω, R2 = 3k Ω, R3 = 5k Ω,
Inductance of coil L = 100 mH = 10 x 10-3 H
Capacitance C = 50 μF = 50 x 10-6 F
Amplitude of AC Voltage Source Um = 240 V
Resistor, coil and capacitor are connected in series
To determine Total Impedance (Z)?
Admittance (Y)
Current Flowing in the circuit Im ? Phase relative to applied voltage ?
Firstly,
As series is connected in parallel, therefore,
1 = 1 + 1 + 1
R R1 R2 R3
= 1 + 1 + 1
1 3 5
= 23/ 15
Or, R = 15/23 = 0.652k Ω = 652 Ω
Frequency (f) = 1 / (2 √LC)ℼ
= 71.18
XL = ωL
= 2ℼfL
= 2 x 71.18 xℼ 100 x 10-3 = 44.70 Ω
and XC = 1/ ωC
= 1/ 2ℼfC
= 1/ 2ℼ x 71.18 x 50 x 10-6
= 44.74 Ω
So, Impedance in the circuit can be calculated by –
Z = 1 .
9

√ 1 + 1 - 1 2
R2 XL XC
= 1 .
√1/6522 + (1/44.70 – 1/44.74)2
= 653.59 Ω
Admittance (Y) = 1 / Z = 0.0015
Current (I) = V/Z
= 240 / 653.59
= 0.367A
Impedance in rectangular form –
1 = 1 + 1 + 1
Z Z1 Z2 Z3
Here,
Z1 = R1 + j (XL – XC)
= 1000 + j (44.70 – 44.74)
= 1000 – 0.4j
1 = 1000 + 0.4j
Z1 1000000.16
Z2 = R2 + j (XL – XC)
= 3000 + j (44.70 – 44.74)
= 3000 – 0.4j
1 = 3000 + 0.4j
Z2 9000000.16
Z3 = R3 + j (XL – XC)
= 5000 + j (44.70 – 44.74)
= 5000 – 0.4j
1 = 5000 + 0.4j
Z1 25000000.16
So,
1 = 1 + 1 + 1
10

Z Z1 Z2 Z3
= 1000 + 0.4j + 3000 + 0.4j + 5000 + 0.4j
1000000.16 9000000.16 25000000.16
11

Activity 3
a) Given, Z1 = 1 + j2
Z2 = 4 – j3
Z3 = -5-j
Solution:
Polar form representation of above complex numbers are –
General polar form of z = (a + jb)
Z = r (cos Ɵ + sin Ɵ)
Where,
r = √a2 + b2
and, Ɵ = tan-1 (b/a)
So, above complex numbers can be represented in following way –
Z1 = 1 + j2
r = √12 + 22 = √5
while, Ɵ = tan-1 (2/1) ≈ 1.11 radian
so,
Z1 = √5 (cos 1.11 + sin 1.11)
Z2 = 4 – j3
r = √42 + 32 = 5
while, Ɵ = tan-1 (-3/4) ≈ 2.50 radian
so,
Z2 = 5 (cos 2.50 + sin 2.50)
Z3 = -5 – j
r = √52 + 12 = √26
while, Ɵ = tan-1 (1/5) ≈ 0.19 ≈ -2.95 radian
so,
Z1 = √26 (cos 2.95 – sin 2.95)
12

b) Z = Z1 + Z1. Z2 – Z3/Z1 in rectangular form
Solution:
Z1. Z2 = (1 + j.2) (4 – j3)
= 4 – j.3 + j.8 – j2 6
= 4 – j.3 + j.8 + 6
= 10 + 5j
Z3/Z1 = (– 5 – j) / (1 + j.2)
Rationalise the denominator –
Z3 = -5 – j x 1 – j.2
Z1 1 + j.2 1 – j.2
So, = (-5 + 10.j – j – 2)
1 – (-2)
= -7 + 9j = -7/3 + j.3
3
Now, Z = Z1 + Z1. Z2 – Z3/Z1
= (1 + j.2) + (10 + 5j) – 7/3 + j.3
= 1 + 10 + 7/3 + j.2 + 5.j – j.3
Z = 40/3 + j.4 (in rectangular form)
c) (-2.5 + j4.2) into exponential form
Complex No. in exponential form –
Z = r ejƟ
Here, r = √a2 + b2
and, Ɵ = tan-1 (b/a)
so, exponential form of (-2.5 + j4.2) can be calculated in following manner –
r = √(-2.5)2 + (4.2)2
= √ 6.25 + 1764
= √1780.25 = 42.19
and, Ɵ = tan-1 (-4.2/2.5) ≈ -1.03 or, 2.11
so, Z = 42.19 ej.2.11
13

d) Z = 4 e1.5 -j.2
Solution: Z = 4 . e1.5 . ej.2
= 4 x 4.48 . ej.2
= 17.92 ej.2
So, in polar form –
Z = r (cos Ɵ + sin Ɵ)
On comparing from above equation, r = 17.92 and Ɵ = 2
So, Z = r (cos Ɵ + sin Ɵ)
= 17.92 (cos 2 + sin 2)
14

Activity 4
De Moivre’s Theorem to determine two square roots of (3 – j4)
Solution: Firstly, express given complex number into polar form as –
Z = (3 – j4)
Here, Absolute value r = √a2 + b2
= √32 + 42 = √25 = 5
and, Argument Ɵ = tan-1 (-4/3) ≈ -53⁰
so, Z = r1/n (cos Ɵ/n + sin Ɵ/n)
For first square root, at r = 2
Z = 51/2 (cos 53 /2 – j sin 53 /2)⁰ ⁰
= 51/2 (cos 26.5 – j sin 26.5)
= 2.23 (0.89 – j 0.98)
Z = (1.98 – j 0.98)
To determine second square root of given complex number, add 360 to Ɵ⁰
Z = 51/2 (cos 413 /2 – j sin 413 /2)⁰ ⁰
= 51/2 (cos 206.5 – j sin 206.5)
= 2.23 (-0.89 + j 0.98)
Z = (-1.98 + j 0.98)
15

Activity 5
De Moivre’s Theorem to prove sin4 Ɵ = ⅛ (cos 4Ɵ – 4 cos 2Ɵ + 3)
Solution: Using De Moivre’s Theorem,
2 j sin Ɵ = (z – 1/z)
or,
(2 j sin Ɵ)4 = (z – 1/z)4
using binomial expression –
8 sin4 Ɵ = (z4 + 1/z4) – 2 (z2 + 1/z2) + 3
taking, (z + 1/z) = 2 cos Ɵ
8 sin4 Ɵ = cos 4 Ɵ – 2 (2cos 2Ɵ) + 3
or,
sin4 Ɵ = ⅛ (cos 4Ɵ – 4 cos 2Ɵ + 3) Hence Proved.
16

Activity 6
Calculate the determinant of
3.1 2.4 6.4
-1.6 3.8 -1.9
5.3 3.4 -4.8
Solution:
Let A = a11 a12 a13
a21 a22 a23
a31 a31 a33
then, value of determinant A can be calculated as
A = a11 ( a22 x a33 – a23 x a31) – a12 ( a21 x a33 – a23 x a31) +a13 (a21 x a31 - a22 x a31)
So,
3.1 2.4 6.4
-1.6 3.8 -1.9
5.3 3.4 -4.8
So,
A = [ 3.1(3.8x-4.8 – (-1.9x3.4)) –2.4 (-1.6x-4.8 – (-1.9x5.3)) + 6.4 (-1.6x3.4 – 3.8x5.3) ]
= 3.1 (-11.78) – 2.4 (17.75) + 6.4 (-25.58)
= -242.49 Answer.
17

Activity 7
Linear Equations –
5T1 + 5T2 + 5T3 = 7.0
T1 + 2T2 + 4T3 = 2.4
4T1 + 2T2 = 4.0
Then Augmented matrix of above linear equation -
5 5 5 T1 = 7.0
A = 1 2 4 T2 = 2.4
4 2 0 T3 = 4.0
Now, using Gaussian Elimination method,
5 5 5 7.0
1 2 4 2.4
4 2 0 4.0
Taking row matrix formula –
R1 →- R⅕ 1
-1 -1 -1 -1.4
1 2 4 2.4
4 2 0 4.0
R2 → R2 + R1
-1 -1 -1 -1.4
0 1 3 1.0
4 2 0 4.0
R3 → ½ R3
-1 -1 -1 -1.4
0 1 3 1.0
2 1 0 2.0
R1 → R1 + R3
1 0 -1 0.6
0 1 3 1.0
2 1 0 2.0
18

R3 → R3 – R1
1 0 -1 0.6
0 1 3 1.0
1 1 1 1.4
R3 ↔ R1
1 1 1 1.4
0 1 3 1.0
1 0 -1 0.6
R1 → R1 – R2
1 0 -2 0.4
0 1 3 1.0
1 0 -1 0.6
R2 → R2 + R1
1 0 -2 0.4
0 1 1 1.4
1 0 -1 0.6
R3 → R3 – R1
1 0 -2 0.4
0 1 1 1.4
0 0 1 0.2
R1 → R1 +2 R3
1 0 0 0.8
0 1 1 1.4
0 0 1 0.2
R2 → R2 – R3
1 0 0 0.8
0 1 0 1.2
0 0 1 0.2
So, T1 = 1.0 , T1 = 1.2 , T3 = 0.2
19

20