Mechanical Vibration Assignment - Analysis of Vibrating Systems

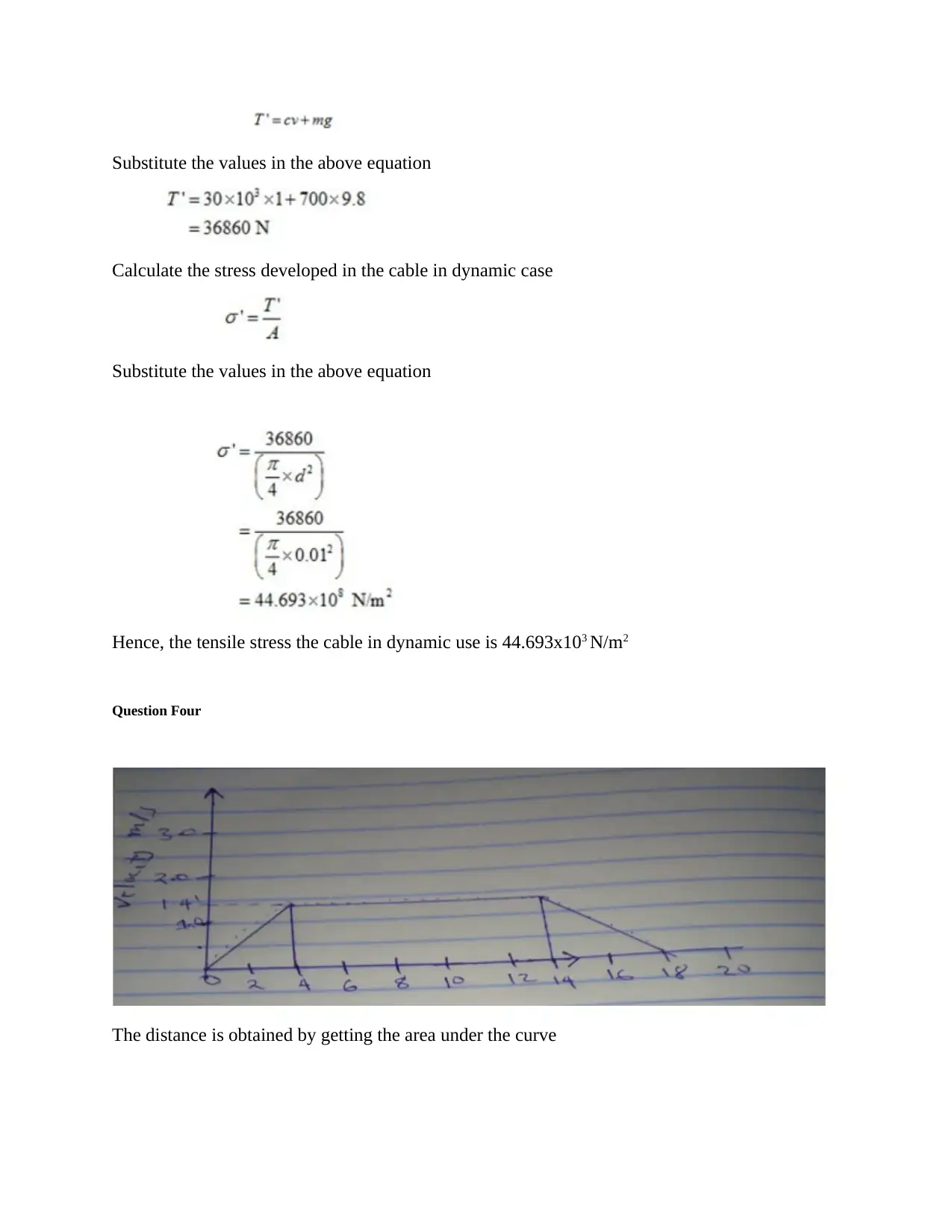
This document presents a comprehensive solution to a mechanical vibration assignment, addressing several key concepts in mechanical engineering. The solution begins with an analysis of energy loss during the impact of a steel ball on a table, considering the coefficient of restitution and the role o...Read More

MECHANICAL VIBRATION
Name of Student
Institution Affiliation

Question one
When the steel ball is falling from a height H, it will have the potential energy of me that is
changed into kinetic energy (Graneau, 2016). Where the ball will touch the table top, its velocity
is given by the following equation (Cracknell, 2014).
Mgh= ½ MV2
V = √2 gh
And when the horizontal table top is fixed and the coefficient of the substitution zero then the
ball will bounce back to the same height (Rhodrigez, 2015). But while the spring with stiffness
constant K plays a very significant role (Serway, 2014). The energy is lost due to expansion and
contraction of the spring when the ball collides with the top of the table (Schampauy, 2012).
If we consider;
E= V 2−V 1
U 1−U 2= coefficient of restitution
Where; U1= initial velocity (velocity of the ball)
U2=velocity of the top table (Taylor, 2014).
V1= Velocity of the ball after collision
V2= Velocity of the table top after the collision (Piombino, 2013).
e= V 2−V 1
U 1
The velocity the ball after collision even where v =velocity of the steel ball after the collision
(Erbele, 2015)

And so on
The total distance covered before stopping
The velocity of the ball decreases due to the loss of energy because of the spring
Question two

Total work done= Kinetic Energy
Question three
From the data given above
Calculate the load acting on the cable in static condition
Mg=T
Substitute the values in the above equation
700 x 9.8=T
T= 6860N
Calculate the elongation in the cable
\ Here, E is the young’s modulus of the steel and A is the cross-
sectional area of the cable.
Substitute the values in above equation
Calculate the stiffness of the cable

Substitute the values in the above equation
Calculate the frequency of the passenger
Substitute the values in the above equation
Hence, the frequency of the passenger is 38.68-1
In static condition, the tension in the cable is T=6860N
Calculate the tensile stress developed in the cable
Substitute the values in above equation
Hence, the tensile stress in the cable in static case is 44.693x108 N/m2
Calculate the tension in the string in the case of dynamic

Substitute the values in the above equation
Calculate the stress developed in the cable in dynamic case
Substitute the values in the above equation
Hence, the tensile stress the cable in dynamic use is 44.693x103 N/m2
Question Four
The distance is obtained by getting the area under the curve

The curve being a trapezium
Question Five

Question five

Question Six
Two blades aircraft can be considered as Bifilar suspension system as shown in the figure
Similarly, three blades aircraft propeller can be considered as trifillen suspension.
Then tension in each wire = w
3

If it is displaced by some small angleƟ
Accelerating torque= Restoring torque
This is similar in Both case hence moment of inertia does not depend on number of wires

Question seven

Question eight

References
Cracknell, D. (2014). Forces of inertia on the object . Leicester : Springer .
Erbele, F. (2015). Uncorvering student idea in science . Washington : NSTA.
Graneau, P. (2016). Newtomiam electrodymics . Chicago: World Scientific .
Piombino, N. (2013). Transistion objects on vibration . Colorado : CRC press.
Rhodrigez, J. (2015). Collage physice : Obtaining the inertia of objects . Stoke : Springer .
Schampauy, D. (2012). The textbook of the inertia of an object . Colorado: Colorado Press.
Serway, R. (2014). College Physics on free fall . London: Springer.
Taylor, C. (2014). Object on free fall . Amsterdam : CRC press.