Electrical Circuit Analysis and Simulation
VerifiedAdded on 2020/05/16
|21
|1576
|140
AI Summary
This assignment focuses on analyzing an electrical circuit using theoretical calculations and practical measurements. It involves determining node potentials, resistance values between pins, and simulating the circuit's behavior under different conditions. Students apply their knowledge of circuit theory to solve problems related to voltage division, current flow, and Ohm's Law. The assignment also includes a comparison between theoretical and measured results, providing insight into the accuracy of calculations and experimental techniques.
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

1
PHYSICS WITH MEDICAL PHYSICS
Name of Student
Institution Affiliation
PHYSICS WITH MEDICAL PHYSICS
Name of Student
Institution Affiliation
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
2
LAB WORK
PART A
A2
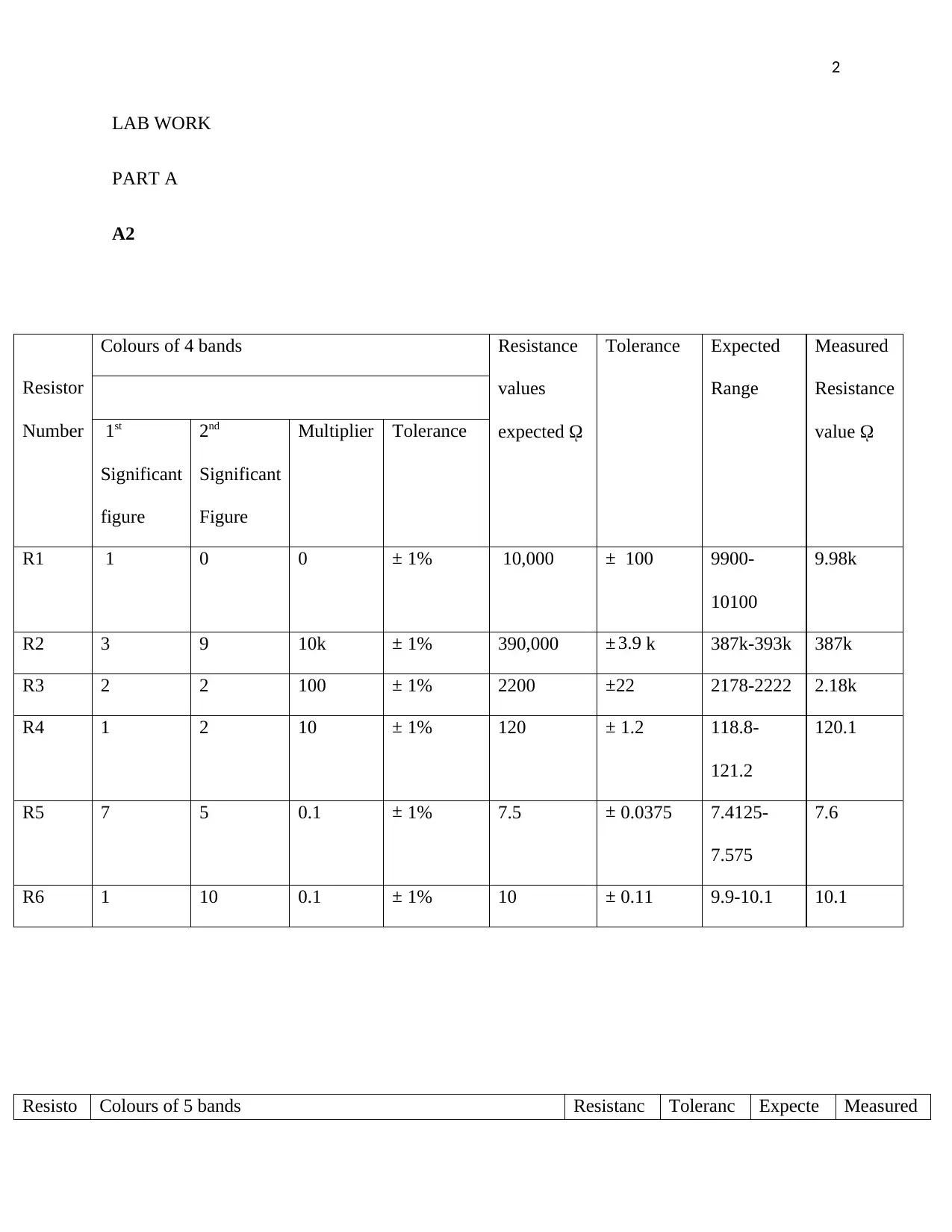
Resistor
Number
Colours of 4 bands Resistance
values
expected ῼ
Tolerance Expected
Range
Measured
Resistance
value ῼ1st
Significant
figure
2nd
Significant
Figure
Multiplier Tolerance
R1 1 0 0 ± 1% 10,000 ± 100 9900-
10100
9.98k
R2 3 9 10k ± 1% 390,000 ± 3.9 k 387k-393k 387k
R3 2 2 100 ± 1% 2200 ±22 2178-2222 2.18k
R4 1 2 10 ± 1% 120 ± 1.2 118.8-
121.2
120.1
R5 7 5 0.1 ± 1% 7.5 ± 0.0375 7.4125-
7.575
7.6
R6 1 10 0.1 ± 1% 10 ± 0.11 9.9-10.1 10.1
Resisto Colours of 5 bands Resistanc Toleranc Expecte Measured
LAB WORK
PART A
A2
Resistor
Number
Colours of 4 bands Resistance
values
expected ῼ
Tolerance Expected
Range
Measured
Resistance
value ῼ1st
Significant
figure
2nd
Significant
Figure
Multiplier Tolerance
R1 1 0 0 ± 1% 10,000 ± 100 9900-
10100
9.98k
R2 3 9 10k ± 1% 390,000 ± 3.9 k 387k-393k 387k
R3 2 2 100 ± 1% 2200 ±22 2178-2222 2.18k
R4 1 2 10 ± 1% 120 ± 1.2 118.8-
121.2
120.1
R5 7 5 0.1 ± 1% 7.5 ± 0.0375 7.4125-
7.575
7.6
R6 1 10 0.1 ± 1% 10 ± 0.11 9.9-10.1 10.1
Resisto Colours of 5 bands Resistanc Toleranc Expecte Measured
3
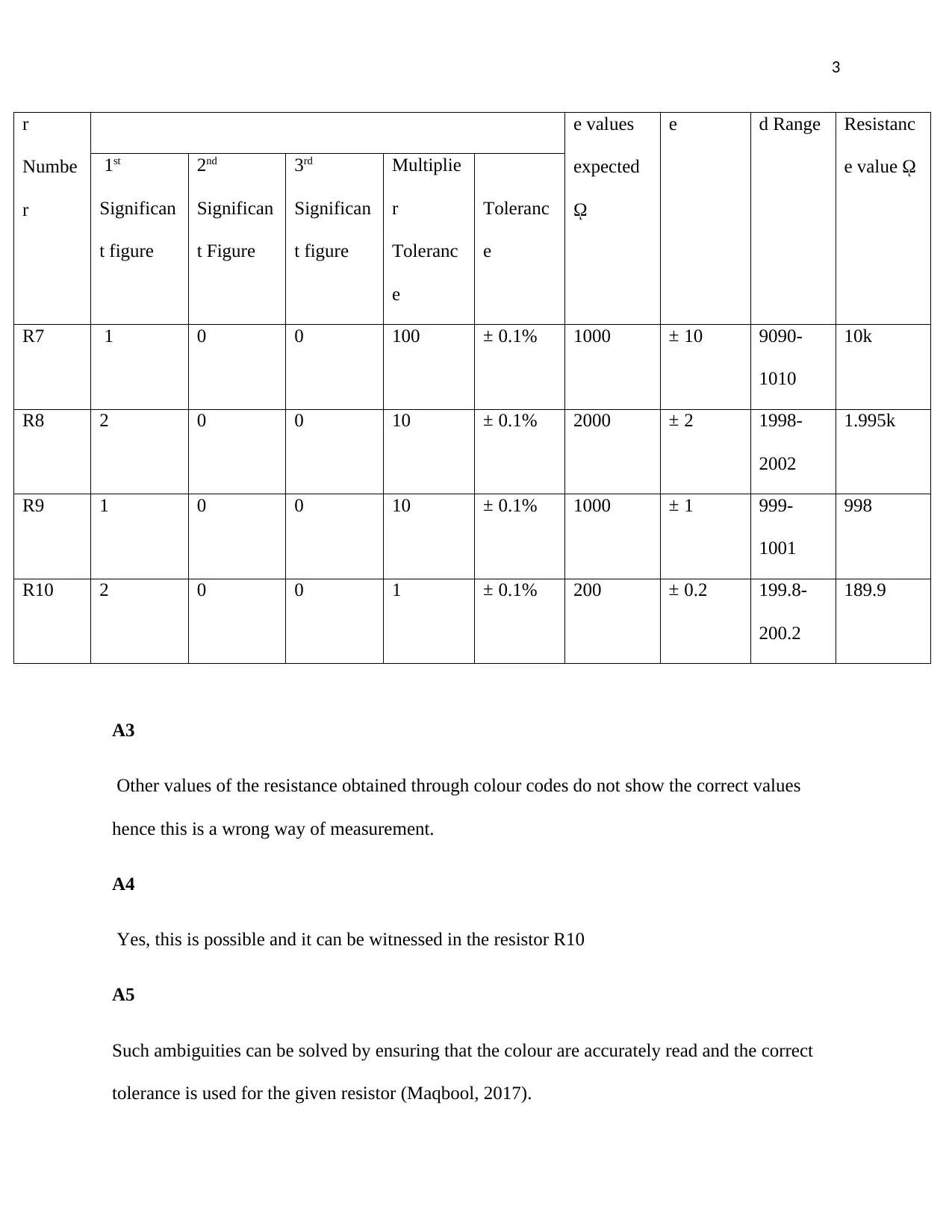
r
Numbe
r
e values
expected
ῼ
e d Range Resistanc
e value ῼ1st
Significan
t figure
2nd
Significan
t Figure
3rd
Significan
t figure
Multiplie
r
Toleranc
e
Toleranc
e
R7 1 0 0 100 ± 0.1% 1000 ± 10 9090-
1010
10k
R8 2 0 0 10 ± 0.1% 2000 ± 2 1998-
2002
1.995k
R9 1 0 0 10 ± 0.1% 1000 ± 1 999-
1001
998
R10 2 0 0 1 ± 0.1% 200 ± 0.2 199.8-
200.2
189.9
A3
Other values of the resistance obtained through colour codes do not show the correct values
hence this is a wrong way of measurement.
A4
Yes, this is possible and it can be witnessed in the resistor R10
A5
Such ambiguities can be solved by ensuring that the colour are accurately read and the correct
tolerance is used for the given resistor (Maqbool, 2017).
r
Numbe
r
e values
expected
ῼ
e d Range Resistanc
e value ῼ1st
Significan
t figure
2nd
Significan
t Figure
3rd
Significan
t figure
Multiplie
r
Toleranc
e
Toleranc
e
R7 1 0 0 100 ± 0.1% 1000 ± 10 9090-
1010
10k
R8 2 0 0 10 ± 0.1% 2000 ± 2 1998-
2002
1.995k
R9 1 0 0 10 ± 0.1% 1000 ± 1 999-
1001
998
R10 2 0 0 1 ± 0.1% 200 ± 0.2 199.8-
200.2
189.9
A3
Other values of the resistance obtained through colour codes do not show the correct values
hence this is a wrong way of measurement.
A4
Yes, this is possible and it can be witnessed in the resistor R10
A5
Such ambiguities can be solved by ensuring that the colour are accurately read and the correct
tolerance is used for the given resistor (Maqbool, 2017).

4
A6
Most values measured were falling within the expected range expect for some resistors like
resistor R 5, the discrepancy witnessed R5 may be due to poor reading of the colours and
inaccurate using of the tolerance for the colour codes (Hose, 2015).
SECTION B.
Pre-Lab work.
B1
The Computer tomography scanner X-ray unlike the normal conventional X-ray, it uses a
motorised x-ray source which rotates around the circular opening of a denut-shaped structure
usually referred to gantly. During the time of application the patient lies on the bed which moves
slowly through the gantly while the X-ray tube rotates around the patient while shooting very
narrow X-ray beams through the body (Maqbool, 2017). The connection of the resistors can be
used in controlling how the X-ray tube rotates by controlling the current which flows to it.
B2
RAB R1 + R2
RBC R2+R3
RCD R3 +R4
RAD R1 +R4
RAC R1 +R3
A6
Most values measured were falling within the expected range expect for some resistors like
resistor R 5, the discrepancy witnessed R5 may be due to poor reading of the colours and
inaccurate using of the tolerance for the colour codes (Hose, 2015).
SECTION B.
Pre-Lab work.
B1
The Computer tomography scanner X-ray unlike the normal conventional X-ray, it uses a
motorised x-ray source which rotates around the circular opening of a denut-shaped structure
usually referred to gantly. During the time of application the patient lies on the bed which moves
slowly through the gantly while the X-ray tube rotates around the patient while shooting very
narrow X-ray beams through the body (Maqbool, 2017). The connection of the resistors can be
used in controlling how the X-ray tube rotates by controlling the current which flows to it.
B2
RAB R1 + R2
RBC R2+R3
RCD R3 +R4
RAD R1 +R4
RAC R1 +R3
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

5
RBD R2 +R4
B3
RAB = R1 + R2
RBC = R2+R3
RCD = R3 +R4
RAD = R1 +R4
RAC = R1 +R3
RBD = R2 +R4
Solving simultaneously;
R1= R2 - RAB
R4 = R2 - RBD
R1 = (R3 - RBC) - RAB
R2 = R3 - RBC
R2 = (R4 - RCD)- RBC
R3 = R4 - RCD
R3 = (R2 - RBD) - RCD
R4 = R2 - RBD
R4 = R2 - RBD
RBD R2 +R4
B3
RAB = R1 + R2
RBC = R2+R3
RCD = R3 +R4
RAD = R1 +R4
RAC = R1 +R3
RBD = R2 +R4
Solving simultaneously;
R1= R2 - RAB
R4 = R2 - RBD
R1 = (R3 - RBC) - RAB
R2 = R3 - RBC
R2 = (R4 - RCD)- RBC
R3 = R4 - RCD
R3 = (R2 - RBD) - RCD
R4 = R2 - RBD
R4 = R2 - RBD

6
R4 = (R3 - RBC) - RBD
B4
Phantom X Phantom Y
RAB 4 Ω 3Ω
RBC 3 Ω 4Ω
RCD 4 Ω 5Ω
RAC 2Ω 3Ω
RAD 4Ω 5Ω
RBD 3Ω 2Ω
B5
RAB = 4 Ω
RBC = 3 Ω
RCD = 4 Ω
RAC = 2Ω
RAD = 4Ω
RBD = 3Ω
R1 = (RCD - RBC) + RAB
= 4 Ω - 3 Ω + 4Ω
R4 = (R3 - RBC) - RBD
B4
Phantom X Phantom Y
RAB 4 Ω 3Ω
RBC 3 Ω 4Ω
RCD 4 Ω 5Ω
RAC 2Ω 3Ω
RAD 4Ω 5Ω
RBD 3Ω 2Ω
B5
RAB = 4 Ω
RBC = 3 Ω
RCD = 4 Ω
RAC = 2Ω
RAD = 4Ω
RBD = 3Ω
R1 = (RCD - RBC) + RAB
= 4 Ω - 3 Ω + 4Ω

7
R1 = 5 Ω
R2 = (RBC + RCD) - RAB
=3 Ω + 4 Ω - 4 Ω
R2 = 3 Ω
R3 = (RBC - RBD) + RCD
R3 = 3 Ω - 3Ω +4 Ω
=4 Ω
R4 = (RCD + RBC) - RBD
R4= 4 Ω + 3 Ω - 3Ω
=4 Ω
B6
R1 = (RCD - RBC) + RAB
R1 = 5Ω - 4Ω + 3Ω
R1= 4Ω
R1 = 5 Ω
R2 = (RBC + RCD) - RAB
=3 Ω + 4 Ω - 4 Ω
R2 = 3 Ω
R3 = (RBC - RBD) + RCD
R3 = 3 Ω - 3Ω +4 Ω
=4 Ω
R4 = (RCD + RBC) - RBD
R4= 4 Ω + 3 Ω - 3Ω
=4 Ω
B6
R1 = (RCD - RBC) + RAB
R1 = 5Ω - 4Ω + 3Ω
R1= 4Ω
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

8
R2 = (RBC + RCD) - RAB
= 4Ω + 5Ω -3Ω
= 6Ω
R3 = (RBC - RBD) + RCD
=4Ω - 5Ω
= 5Ω
R4 = (RCD + RBC) - RBD
=5Ω + 4Ω -2Ω
= 7 Ω
B7
RAB = RW.(RX +RY +RZ)
RW + RX + RY + RZ
RBC =RX.( RW +RY +RZ)
RX + RW+ RY + RZ
RCD = RY.( RW +RX +RZ)
RY + RW+ RX + RZ
R2 = (RBC + RCD) - RAB
= 4Ω + 5Ω -3Ω
= 6Ω
R3 = (RBC - RBD) + RCD
=4Ω - 5Ω
= 5Ω
R4 = (RCD + RBC) - RBD
=5Ω + 4Ω -2Ω
= 7 Ω
B7
RAB = RW.(RX +RY +RZ)
RW + RX + RY + RZ
RBC =RX.( RW +RY +RZ)
RX + RW+ RY + RZ
RCD = RY.( RW +RX +RZ)
RY + RW+ RX + RZ

9
RAD = RZ.( RW +RX +RY
RZ + RW+ RX + RY
RAC =RX.( RW +RY +RZ)
RX + RW+ RY + RZ
RCD = RX.( RW +RY +RZ)
RY + RW+ RX + RZ
B9
RAD = RZ.( RW +RX +RY
RZ + RW+ RX + RY
RAC =RX.( RW +RY +RZ)
RX + RW+ RY + RZ
RCD = RX.( RW +RY +RZ)
RY + RW+ RX + RZ
B9

10
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

11
B10
Ensuring a good test.
First one is required to test the resistance on the components and not in the test in the circuit.
Once the resistance of a component is measured while in the circuit there is a great possibility of
getting in correct data (Hose, 2015).
Only the components which are turned off are to be tested.
B10
Ensuring a good test.
First one is required to test the resistance on the components and not in the test in the circuit.
Once the resistance of a component is measured while in the circuit there is a great possibility of
getting in correct data (Hose, 2015).
Only the components which are turned off are to be tested.

12
All the capacitors in the circuit which are to be tested should be discharged before testing. The
discharged capacitors can absorb charge from the multimeter’s current which will result in a
momentary fluctuations of the results.
One should check for the diodes in the circuit. And determine the resistance which is recorded.
B11
Phantom z
RAB 3 Ω
RBC 6Ω
RCD 4 Ω
RAC 3 Ω
RAD 4 Ω
RBD 3 Ω
B12
R1 = (RCD - RBC) + RAB
= 4 Ω - 3 Ω + 4Ω
R1 = 5 Ω
R2 = (RBC + RCD) - RAB
=3 Ω + 4 Ω - 4 Ω
All the capacitors in the circuit which are to be tested should be discharged before testing. The
discharged capacitors can absorb charge from the multimeter’s current which will result in a
momentary fluctuations of the results.
One should check for the diodes in the circuit. And determine the resistance which is recorded.
B11
Phantom z
RAB 3 Ω
RBC 6Ω
RCD 4 Ω
RAC 3 Ω
RAD 4 Ω
RBD 3 Ω
B12
R1 = (RCD - RBC) + RAB
= 4 Ω - 3 Ω + 4Ω
R1 = 5 Ω
R2 = (RBC + RCD) - RAB
=3 Ω + 4 Ω - 4 Ω

13
R2 = 3 Ω
R3 = (RBC - RBD) + RCD
R3 = 3 Ω - 3Ω +4 Ω
=4 Ω
R4 = (RCD + RBC) - RBD
R4= 4 Ω + 3 Ω - 3Ω
=4 Ω
SECTION C
C1
From V0= I1R1+I2R2 …………..
But I1= V 1
Rt
V0= V 1 R 1
Rt + V 2 R 2
Rt + ……………………
V0 = [ V 1
R1 + V 2
R 2 + V 3
R 3 ] × ( R1+R2+R3) ………………………………………………… i
R2 = 3 Ω
R3 = (RBC - RBD) + RCD
R3 = 3 Ω - 3Ω +4 Ω
=4 Ω
R4 = (RCD + RBC) - RBD
R4= 4 Ω + 3 Ω - 3Ω
=4 Ω
SECTION C
C1
From V0= I1R1+I2R2 …………..
But I1= V 1
Rt
V0= V 1 R 1
Rt + V 2 R 2
Rt + ……………………
V0 = [ V 1
R1 + V 2
R 2 + V 3
R 3 ] × ( R1+R2+R3) ………………………………………………… i
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

14
The above equation I can be rearranged to the below equation through dividing by the reciprocal
V0= [ V 1
R 1 + V 2
R 2 + V 3
R 3 + … VN
RN ]
[ 1
R 1 + 1
R 2 + 1
R3 +… 1
RN ]
V0= [ V 1
R 1 + V 2
R 2 + V 3
R 3 + … VN
RN ]
[ 1
R 1 + 1
R 2 + 1
R3 +… 1
RN ]
C2
From V0= [ V 1
R 1 + V 2
R 2 + V 3
R 3 +… VN
RN ]
[ 1
R 1 + 1
R 2 + 1
R3 +… 1
RN ] we are able to solve this problem, the value of R is taken
to be the same for all.
V0= [ V 1
R + V 2
R + V 3
R + … VN
RN ]
[ 1
R 1 + 1
R 2 + 1
R3 +… 1
RN ]
The above equation I can be rearranged to the below equation through dividing by the reciprocal
V0= [ V 1
R 1 + V 2
R 2 + V 3
R 3 + … VN
RN ]
[ 1
R 1 + 1
R 2 + 1
R3 +… 1
RN ]
V0= [ V 1
R 1 + V 2
R 2 + V 3
R 3 + … VN
RN ]
[ 1
R 1 + 1
R 2 + 1
R3 +… 1
RN ]
C2
From V0= [ V 1
R 1 + V 2
R 2 + V 3
R 3 +… VN
RN ]
[ 1
R 1 + 1
R 2 + 1
R3 +… 1
RN ] we are able to solve this problem, the value of R is taken
to be the same for all.
V0= [ V 1
R + V 2
R + V 3
R + … VN
RN ]
[ 1
R 1 + 1
R 2 + 1
R3 +… 1
RN ]

15
V0= [ 1
R (V 1+V 2+ V 3+ … VN) ]
[ 1
R (1+1+1+… 1) ]
V0= V 1+V 2+V 3
1+1+1
V0 = V 1+V 2+V 3
3
Therefore when the value of the resistor are the same then the output voltage is the average
voltage.
C3
V0= [ 1
R (V 1+V 2+ V 3+ … VN) ]
[ 1
R (1+1+1+… 1) ]
V0= V 1+V 2+V 3
1+1+1
V0 = V 1+V 2+V 3
3
Therefore when the value of the resistor are the same then the output voltage is the average
voltage.
C3

16
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

17
C4
There are two resistor in each loop hence
Vx= VA
R 1 + VC
R 1 + VD
R 1 + VE
R 1 + VF
R 1
The value of the resistance is equal in each loop hence
Vx =
1
R [ V
5 + V
5 + V
5 + V
5 + V
5 ]
2
R [ 1+1+1+1+1 ]
Vx= [ 3 V
5 + 2V
5 ]
2(5)
C4
There are two resistor in each loop hence
Vx= VA
R 1 + VC
R 1 + VD
R 1 + VE
R 1 + VF
R 1
The value of the resistance is equal in each loop hence
Vx =
1
R [ V
5 + V
5 + V
5 + V
5 + V
5 ]
2
R [ 1+1+1+1+1 ]
Vx= [ 3 V
5 + 2V
5 ]
2(5)

18
Vx= V
10
C5
The value of voltage is the potential difference between the two points
VGA= ++ V
2 -0 = + V
2 volts
VGB = +Vx – 0 =+ Vx volts
VGC =-Vx – 0 = -Vx volts
VGE = - Vx – 0 = -Vx volts
VGF = +Vx – 0 =+ Vx volts
VGD = -+ V
2 -0 = −V
2 volts
C6
For resistance connected in parallel
Vx= V
10
C5
The value of voltage is the potential difference between the two points
VGA= ++ V
2 -0 = + V
2 volts
VGB = +Vx – 0 =+ Vx volts
VGC =-Vx – 0 = -Vx volts
VGE = - Vx – 0 = -Vx volts
VGF = +Vx – 0 =+ Vx volts
VGD = -+ V
2 -0 = −V
2 volts
C6
For resistance connected in parallel

19
1
RT = 1
R 1 + 1
R 2
But R1 = R and R2 = x.R
Therefore; 1
RT = 1
R + 1
x . R
1
RT = xR + R
R (xR)
1
RT = R
R [ x+ 1
xR ]
1
RT = [ x +1
xR ]
RT= xR
1+ x
RT= [ x
1+ x ] R
C7
1
RT = 1
R 1 + 1
R 2
But R1 = R and R2 = x.R
Therefore; 1
RT = 1
R + 1
x . R
1
RT = xR + R
R (xR)
1
RT = R
R [ x+ 1
xR ]
1
RT = [ x +1
xR ]
RT= xR
1+ x
RT= [ x
1+ x ] R
C7
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

20
C8
Vy = VR
RT
And Vy = ½( VR
2 )
¿ ¿
But since there are six similar loops the above equation will appear as below
Vy= V . x
4 x +6
This can be further reduced as below;
Vy= Vx
2(2 x +3)
c9.
R2 x Calculated Vy The value of Vy decreases as the
100 KΩ 5 0.192 V
C8
Vy = VR
RT
And Vy = ½( VR
2 )
¿ ¿
But since there are six similar loops the above equation will appear as below
Vy= V . x
4 x +6
This can be further reduced as below;
Vy= Vx
2(2 x +3)
c9.
R2 x Calculated Vy The value of Vy decreases as the
100 KΩ 5 0.192 V

21
scaling factor x is reduced25 KΩ 1 0.1 V
1 KΩ 0.5 0.0625 V
200 Ω 0.1 0.015625 V
100 Ω 0.05 0.00161 V
c10.
R2 % decrease in Vy The value of Vy decreases as compared to the
initial uniform situation for each of the
different values of R
2 KΩ 0
1 KΩ 0.9
200 Ω 3.0
100 Ω 8.0
c11.
R = 2 kΩ
One triangular element has 3 resistors in parallel
Therefore equivalent resistance RT= x
1+ x × R
Thus RT = 3
1+ 3 ×2
=0.75 × 2
= 1.5 kΩ
The above calculation is almost similar to the measured value
scaling factor x is reduced25 KΩ 1 0.1 V
1 KΩ 0.5 0.0625 V
200 Ω 0.1 0.015625 V
100 Ω 0.05 0.00161 V
c10.
R2 % decrease in Vy The value of Vy decreases as compared to the
initial uniform situation for each of the
different values of R
2 KΩ 0
1 KΩ 0.9
200 Ω 3.0
100 Ω 8.0
c11.
R = 2 kΩ
One triangular element has 3 resistors in parallel
Therefore equivalent resistance RT= x
1+ x × R
Thus RT = 3
1+ 3 ×2
=0.75 × 2
= 1.5 kΩ
The above calculation is almost similar to the measured value
1 out of 21
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.