MU123 Discovering Mathematics: TMA 04 - Applied Math Problems
VerifiedAdded on 2023/06/11
|9
|1422
|422
Homework Assignment
AI Summary
This assignment solution for MU123 Discovering Mathematics TMA 04 covers a range of mathematical concepts and applications. It includes solving a quadratic equation representing the trajectory of a tennis ball, determining x and y intercepts, finding the vertex, and sketching the trajectory. It also involves solving quadratic equations, analyzing transportation data using statistical measures and histograms, applying trigonometric principles to calculate lengths and angles, and correcting trigonometric solutions. The document concludes with a reflection on the algebraic skills learned and how to improve confidence and accuracy in mathematical problem-solving. Desklib offers a vast collection of similar solved assignments and past papers to aid students in their studies.

MU123 Discovering mathematics
Faculty of Science, Technology, Engineering and Mathematics
TMA 04
1. Trajectory of a tennis
a) Given the trajectory is a parabola with the following equation
y=−x2
8 + 11 x
8 +3
2 (1.1)
i) The parabola n-shaped, since a< 0 if the equation is given in the form of
equation (1.2) below
y=a x2 +bx +c (1.2)
ii) The x-intercept, y=0, thus equation (1.1) is given as:
−x2
8 +11 x
8 + 3
2 =0x=−b ± √b2−4 ac
2 a ¿
−11
8 ± √ ( 11
8 )
2
−4 ×− 1
8 × 3
2
−2
8
∴ x=12∨x=−1
Thus the x-intercepts are (12, 0) and (-1, 0); considering the tennis ball, the x-
intercept (the position where the ball hits the ground) is 12.
iii) The y-intercept is when x=0, if x is replaced by zero in equation (1.1), then the y-
intercept is 3
2
iv) Rewriting equation (1.1) in the form of a ( x−h )2+k by use of completing square,
gives −1
8 ( x −11
2 )
2
+ 169
32 (1.3)
Faculty of Science, Technology, Engineering and Mathematics
TMA 04
1. Trajectory of a tennis
a) Given the trajectory is a parabola with the following equation
y=−x2
8 + 11 x
8 +3
2 (1.1)
i) The parabola n-shaped, since a< 0 if the equation is given in the form of
equation (1.2) below
y=a x2 +bx +c (1.2)
ii) The x-intercept, y=0, thus equation (1.1) is given as:
−x2
8 +11 x
8 + 3
2 =0x=−b ± √b2−4 ac
2 a ¿
−11
8 ± √ ( 11
8 )
2
−4 ×− 1
8 × 3
2
−2
8
∴ x=12∨x=−1
Thus the x-intercepts are (12, 0) and (-1, 0); considering the tennis ball, the x-
intercept (the position where the ball hits the ground) is 12.
iii) The y-intercept is when x=0, if x is replaced by zero in equation (1.1), then the y-
intercept is 3
2
iv) Rewriting equation (1.1) in the form of a ( x−h )2+k by use of completing square,
gives −1
8 ( x −11
2 )
2
+ 169
32 (1.3)
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
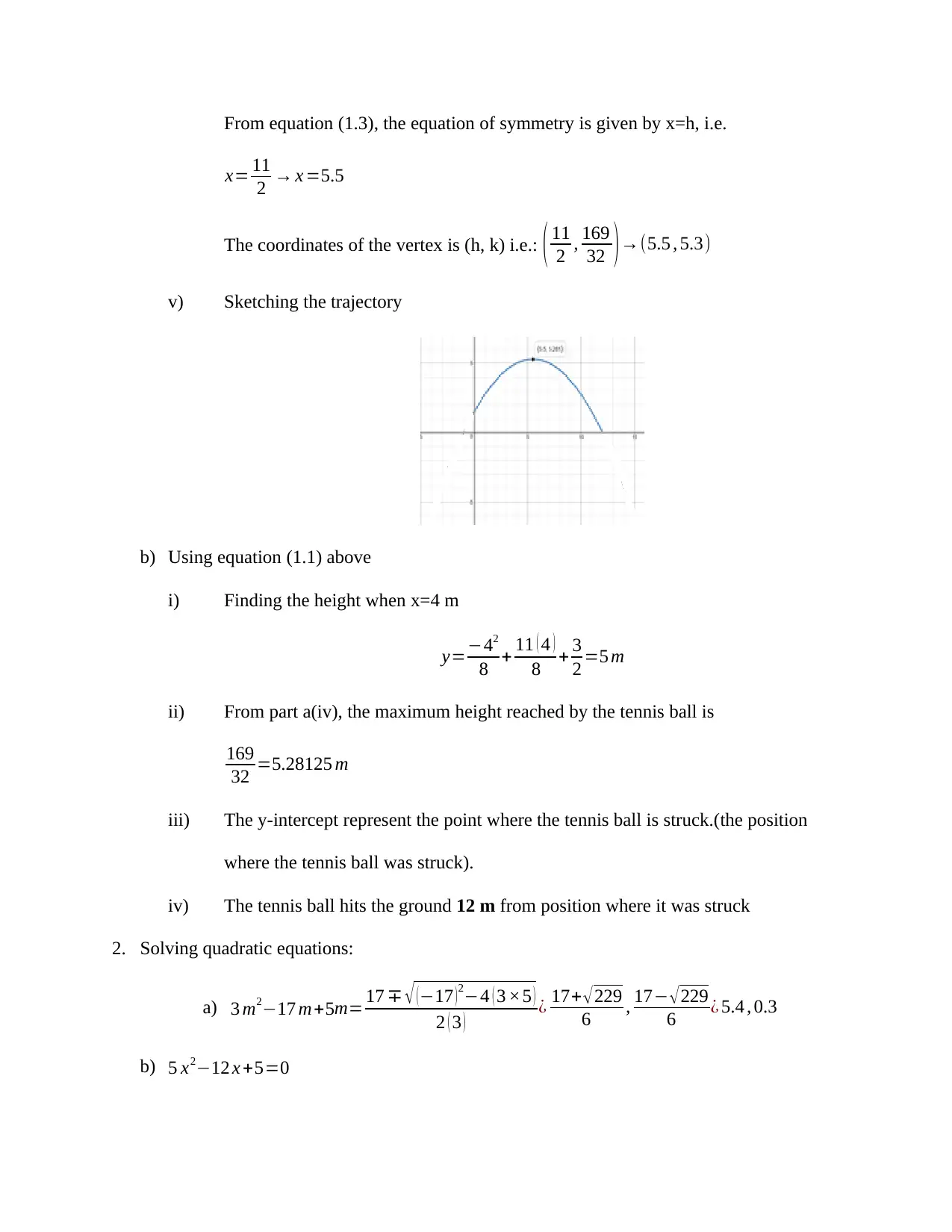
From equation (1.3), the equation of symmetry is given by x=h, i.e.
x= 11
2 → x =5.5
The coordinates of the vertex is (h, k) i.e.: ( 11
2 , 169
32 )→(5.5 , 5.3)
v) Sketching the trajectory
b) Using equation (1.1) above
i) Finding the height when x=4 m
y=−42
8 + 11 ( 4 )
8 + 3
2 =5 m
ii) From part a(iv), the maximum height reached by the tennis ball is
169
32 =5.28125 m
iii) The y-intercept represent the point where the tennis ball is struck.(the position
where the tennis ball was struck).
iv) The tennis ball hits the ground 12 m from position where it was struck
2. Solving quadratic equations:
a) 3 m2−17 m+5m= 17 ∓ √ (−17 )2−4 ( 3 ×5 )
2 ( 3 ) ¿ 17+ √229
6 , 17− √229
6 ¿ 5.4 , 0.3
b) 5 x2−12 x +5=0
x= 11
2 → x =5.5
The coordinates of the vertex is (h, k) i.e.: ( 11
2 , 169
32 )→(5.5 , 5.3)
v) Sketching the trajectory
b) Using equation (1.1) above
i) Finding the height when x=4 m
y=−42
8 + 11 ( 4 )
8 + 3
2 =5 m
ii) From part a(iv), the maximum height reached by the tennis ball is
169
32 =5.28125 m
iii) The y-intercept represent the point where the tennis ball is struck.(the position
where the tennis ball was struck).
iv) The tennis ball hits the ground 12 m from position where it was struck
2. Solving quadratic equations:
a) 3 m2−17 m+5m= 17 ∓ √ (−17 )2−4 ( 3 ×5 )
2 ( 3 ) ¿ 17+ √229
6 , 17− √229
6 ¿ 5.4 , 0.3
b) 5 x2−12 x +5=0

i) Discriminant D= ( −12 ) 2− ( 4 × 5 ×5 ) =44
ii) Since D>0, the solution has two (2) distinct real roots
iii) The graph is U-shaped, and cutting x-axis in two different points
c) x2−18 x−9
i) In completed-square form.
x2−18 x+ ( 18
2 )
2
=9+( 18
2 )
2
( x−9 ) 2=90
ii) Solving
x−9=± √ 90=± 3 √10 x=9 ± 3 √ 10x=9+3 √10 , x=9−3 √10
iii) The vertex of ( x−9 )2−90 is (9, -90)
3. Transportation
a) Entering the given data into two lists in Data-plotter (Here Excel is used)
Public Transport Private Transport
23 30
25 32
25 33
25 34
26 33
26 36
29 37
30 34
31 37
31 36
32 39
33 38
33 41
34 44
34 38
36 41
36 40
37 45
42 45
43 44
ii) Since D>0, the solution has two (2) distinct real roots
iii) The graph is U-shaped, and cutting x-axis in two different points
c) x2−18 x−9
i) In completed-square form.
x2−18 x+ ( 18
2 )
2
=9+( 18
2 )
2
( x−9 ) 2=90
ii) Solving
x−9=± √ 90=± 3 √10 x=9 ± 3 √ 10x=9+3 √10 , x=9−3 √10
iii) The vertex of ( x−9 )2−90 is (9, -90)
3. Transportation
a) Entering the given data into two lists in Data-plotter (Here Excel is used)
Public Transport Private Transport
23 30
25 32
25 33
25 34
26 33
26 36
29 37
30 34
31 37
31 36
32 39
33 38
33 41
34 44
34 38
36 41
36 40
37 45
42 45
43 44
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

b) From the data above:
i) The average travel time of Public Transport is less than the average travel tim of
Private Transport. The average travel time for Public transport is 31.55 while that
of Private Transport is 37.88 (Values are as depicted by data plotter used)
ii) The data is more spread out for using Public Transport than using Private
Transport. Since the standard deviation of Public Transport is 5.6145956 while
that of Private Transport is 4.49883025. (Values are as depicted by data plotter
used)
c) Data are skewed; skewed to the left since the mean/average is less that the medium.
There is a small different between the average and the medium. Furthermore, the data is
left skewed because the medium is closer to the third quartile than in the first quartile.
d) Histogram creating
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
20
25
30
35
40
45
Company Transport
Public Transport Private Transport
i) The average travel time of Public Transport is less than the average travel tim of
Private Transport. The average travel time for Public transport is 31.55 while that
of Private Transport is 37.88 (Values are as depicted by data plotter used)
ii) The data is more spread out for using Public Transport than using Private
Transport. Since the standard deviation of Public Transport is 5.6145956 while
that of Private Transport is 4.49883025. (Values are as depicted by data plotter
used)
c) Data are skewed; skewed to the left since the mean/average is less that the medium.
There is a small different between the average and the medium. Furthermore, the data is
left skewed because the medium is closer to the third quartile than in the first quartile.
d) Histogram creating
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
20
25
30
35
40
45
Company Transport
Public Transport Private Transport
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

e) In the histogram, the travel time for Private Transport takes longer time than that of
Public Transport can be seen more clearly as compared to box plot.
4. Trigonometry.
a) Using figure 1:Length of side marked with x
cos ( 39 )= x
26 x=26 cos (39 )=20.205795 cm=20 cm
b) QR =32.4 cm, PQ=28.3 cm
x=∠ QRP=arctan ( 28.3
32.4 )∠QRP=41.1328 °=41°
c) Using figure 2
i) Angle ABC
Using cosine rule:
cos ( B ) =a2+ c2−b2
2 ac = 4.62 + 9.32−12.22
2 × 4.6× 9.3 =−0.51501
∠ ABC=cos−1 (−0.51501 )=120.9977¿ 121°
ii) Area of triangle ABC
Using Heron’s formula
A= √ p ( p−a ) ( p−b ) ( p−c ) p= 9.3+12.2+4.6
2 = 26.1
2 =13.05
A= √13.05 ( 8.45 ) ( 0.85 ) ( 3.75 )=351.4935938c m2¿ 351 c m2
Public Transport can be seen more clearly as compared to box plot.
4. Trigonometry.
a) Using figure 1:Length of side marked with x
cos ( 39 )= x
26 x=26 cos (39 )=20.205795 cm=20 cm
b) QR =32.4 cm, PQ=28.3 cm
x=∠ QRP=arctan ( 28.3
32.4 )∠QRP=41.1328 °=41°
c) Using figure 2
i) Angle ABC
Using cosine rule:
cos ( B ) =a2+ c2−b2
2 ac = 4.62 + 9.32−12.22
2 × 4.6× 9.3 =−0.51501
∠ ABC=cos−1 (−0.51501 )=120.9977¿ 121°
ii) Area of triangle ABC
Using Heron’s formula
A= √ p ( p−a ) ( p−b ) ( p−c ) p= 9.3+12.2+4.6
2 = 26.1
2 =13.05
A= √13.05 ( 8.45 ) ( 0.85 ) ( 3.75 )=351.4935938c m2¿ 351 c m2
d) Degree and Rad
i) 48 ° = 48
180 π rad = 4 π
15 rad
ii) Area of the sector
A=1
2 ( θ r2 )= 1
2 × 4
15 π ×6.82 =19.368966 c m2
¿ 19 c m2 ¿ 2 sf
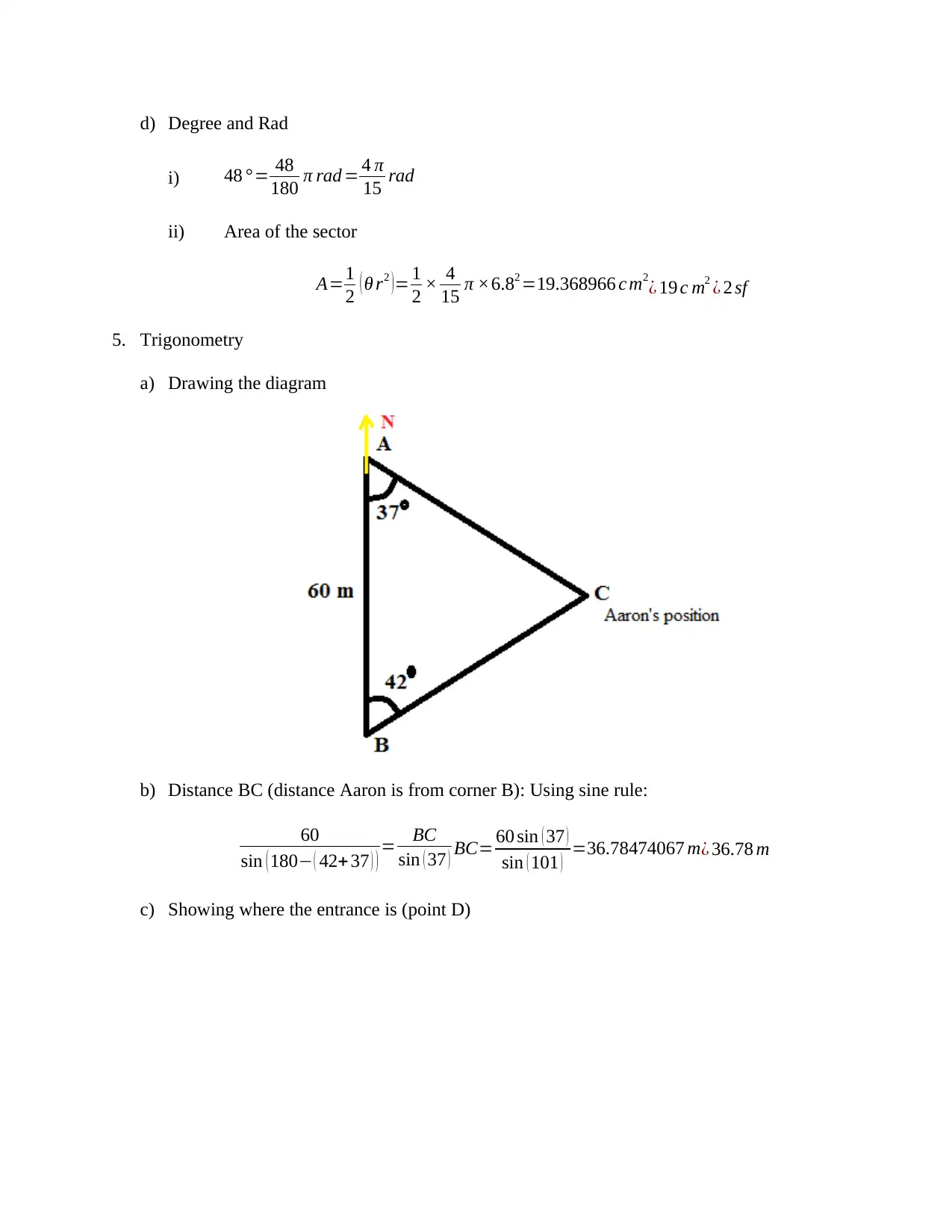
5. Trigonometry
a) Drawing the diagram
b) Distance BC (distance Aaron is from corner B): Using sine rule:
60
sin ( 180− ( 42+ 37 ) ) = BC
sin ( 37 ) BC= 60 sin ( 37 )
sin ( 101 ) =36.78474067 m¿ 36.78 m
c) Showing where the entrance is (point D)
i) 48 ° = 48
180 π rad = 4 π
15 rad
ii) Area of the sector
A=1
2 ( θ r2 )= 1
2 × 4
15 π ×6.82 =19.368966 c m2
¿ 19 c m2 ¿ 2 sf
5. Trigonometry
a) Drawing the diagram
b) Distance BC (distance Aaron is from corner B): Using sine rule:
60
sin ( 180− ( 42+ 37 ) ) = BC
sin ( 37 ) BC= 60 sin ( 37 )
sin ( 101 ) =36.78474067 m¿ 36.78 m
c) Showing where the entrance is (point D)
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
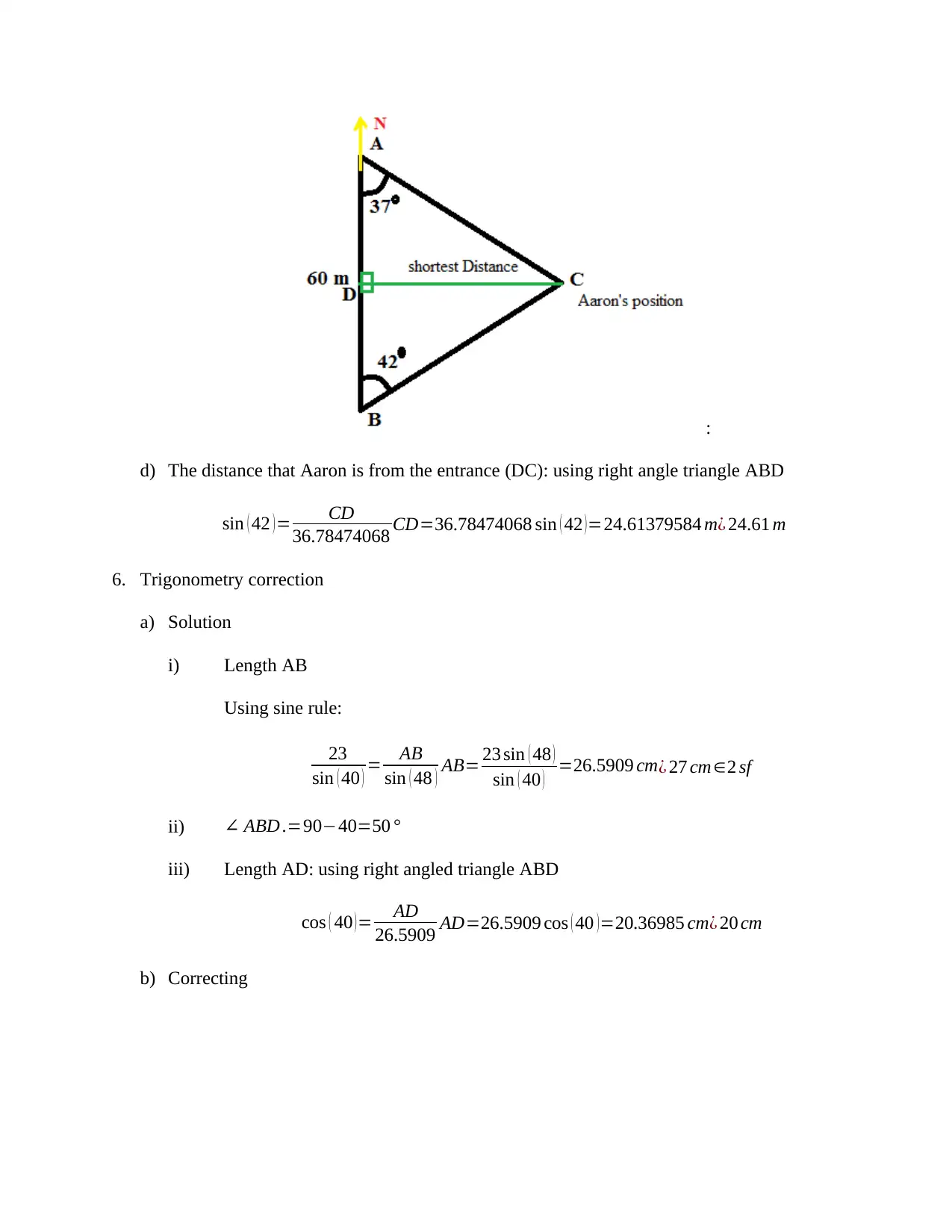
:
d) The distance that Aaron is from the entrance (DC): using right angle triangle ABD
sin ( 42 ) = CD
36.78474068 CD=36.78474068 sin ( 42 ) =24.61379584 m¿ 24.61 m
6. Trigonometry correction
a) Solution
i) Length AB
Using sine rule:
23
sin ( 40 ) = AB
sin ( 48 ) AB= 23 sin ( 48 )
sin ( 40 ) =26.5909 cm ¿ 27 cm ∈2 sf
ii) ∠ ABD .=90−40=50 °
iii) Length AD: using right angled triangle ABD
cos ( 40 )= AD
26.5909 AD=26.5909 cos ( 40 ) =20.36985 cm¿ 20 cm
b) Correcting
d) The distance that Aaron is from the entrance (DC): using right angle triangle ABD
sin ( 42 ) = CD
36.78474068 CD=36.78474068 sin ( 42 ) =24.61379584 m¿ 24.61 m
6. Trigonometry correction
a) Solution
i) Length AB
Using sine rule:
23
sin ( 40 ) = AB
sin ( 48 ) AB= 23 sin ( 48 )
sin ( 40 ) =26.5909 cm ¿ 27 cm ∈2 sf
ii) ∠ ABD .=90−40=50 °
iii) Length AD: using right angled triangle ABD
cos ( 40 )= AD
26.5909 AD=26.5909 cos ( 40 ) =20.36985 cm¿ 20 cm
b) Correcting
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

7. Themes met in MU123
a) The chosen in this part is algebraic skills. Knowing the rules and the laws governing the
relationships in calculation, it becomes easier and simple in calculation. For example in
the topic of trigonometry, I can work well and confidently. On the other hand, working
with data sometimes become challenging if the given data is very large. This require high
performing computer software to handle the data. Furthermore, during data transfer,
errors may arise resulting to wrong calculations. One is also able to check/verify the work
a) The chosen in this part is algebraic skills. Knowing the rules and the laws governing the
relationships in calculation, it becomes easier and simple in calculation. For example in
the topic of trigonometry, I can work well and confidently. On the other hand, working
with data sometimes become challenging if the given data is very large. This require high
performing computer software to handle the data. Furthermore, during data transfer,
errors may arise resulting to wrong calculations. One is also able to check/verify the work

b) Steps that can help to work confidently are:
i) Use of high accuracy computer software. This may help to reduce calculation
error especially when large data is used
ii) Use of software that are capable of tracking the initial data and the final data used,
to reduce the error of data transfer
c) An example where I verified my work is when determining the adjacent length of a right
angled triangle (Question 4(a)). Two (2) methods can be used to verify the length, i.e. the
Pythagoras theorem or by use Sine rule. Both method should arrive to same answer.
i) Use of high accuracy computer software. This may help to reduce calculation
error especially when large data is used
ii) Use of software that are capable of tracking the initial data and the final data used,
to reduce the error of data transfer
c) An example where I verified my work is when determining the adjacent length of a right
angled triangle (Question 4(a)). Two (2) methods can be used to verify the length, i.e. the
Pythagoras theorem or by use Sine rule. Both method should arrive to same answer.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 9
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.



