Predicting Summer Rainfall: Multiple Regression Analysis of Crop Data

This assignment presents a multiple regression analysis conducted using MS-Excel to predict the relationship between summer rainfall, growing season rainfall, and wheat yield. The analysis aims to determine the impact of growing season rainfall and wheat yield on summer rainfall. The student u...Read More

Running head: MULTIPLE REGRESSION ANALYSIS 1
Does the Amount of Rainfall for Growing Season and Wheat Yield Affect Summer Rainfall
significantly?
Student Name
Institution

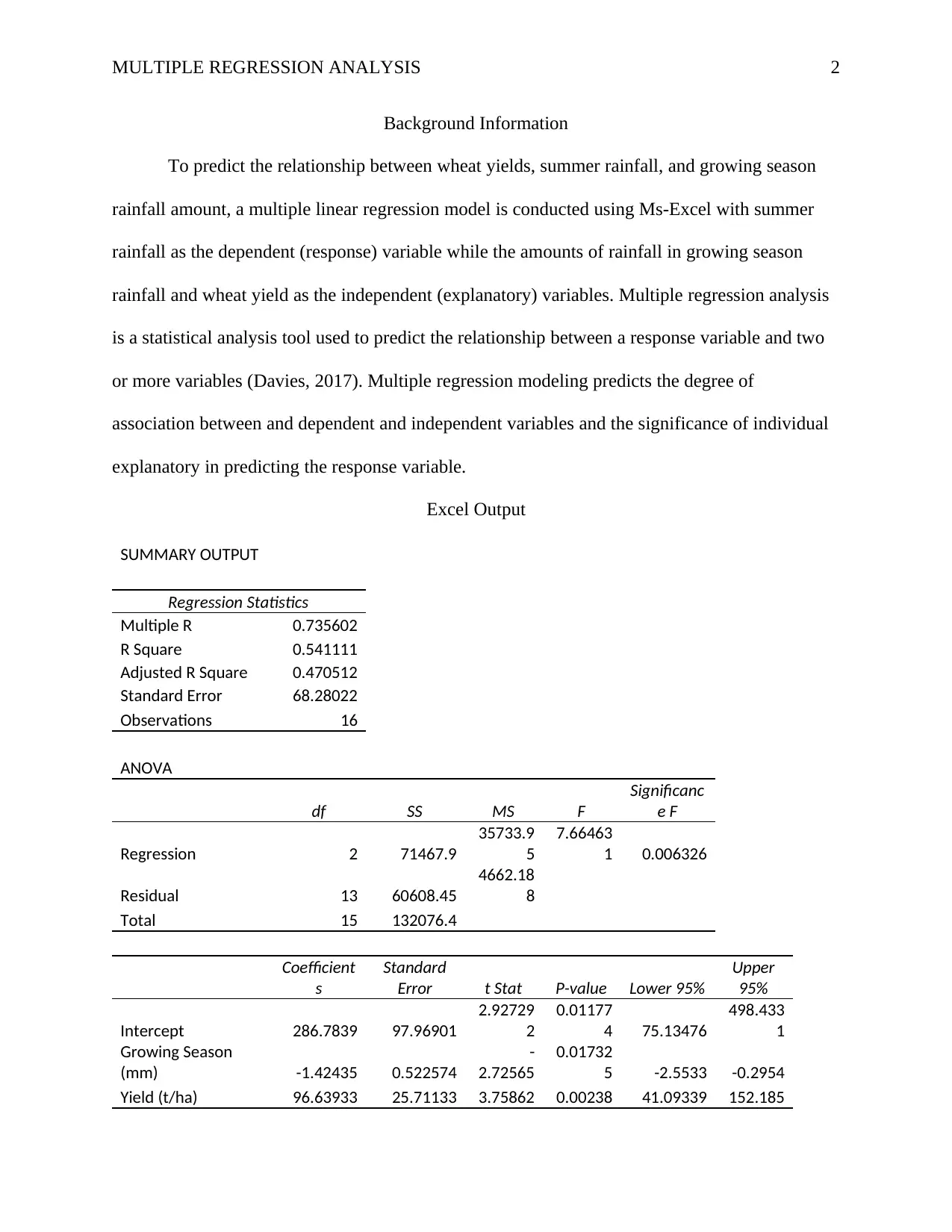
MULTIPLE REGRESSION ANALYSIS 2
Background Information
To predict the relationship between wheat yields, summer rainfall, and growing season
rainfall amount, a multiple linear regression model is conducted using Ms-Excel with summer
rainfall as the dependent (response) variable while the amounts of rainfall in growing season
rainfall and wheat yield as the independent (explanatory) variables. Multiple regression analysis
is a statistical analysis tool used to predict the relationship between a response variable and two
or more variables (Davies, 2017). Multiple regression modeling predicts the degree of
association between and dependent and independent variables and the significance of individual
explanatory in predicting the response variable.
Excel Output
SUMMARY OUTPUT
Regression Statistics
Multiple R 0.735602
R Square 0.541111
Adjusted R Square 0.470512
Standard Error 68.28022
Observations 16
ANOVA
df SS MS F
Significanc
e F
Regression 2 71467.9
35733.9
5
7.66463
1 0.006326
Residual 13 60608.45
4662.18
8
Total 15 132076.4
Coefficient
s
Standard
Error t Stat P-value Lower 95%
Upper
95%
Intercept 286.7839 97.96901
2.92729
2
0.01177
4 75.13476
498.433
1
Growing Season
(mm) -1.42435 0.522574
-
2.72565
0.01732
5 -2.5533 -0.2954
Yield (t/ha) 96.63933 25.71133 3.75862 0.00238 41.09339 152.185

MULTIPLE REGRESSION ANALYSIS 3
9 8 3
Results
The coefficients of the fitted regression model are 286.7839, -1.42435, and 96.63933 for
constants(y-intercept), growing season rainfall, and wheat yield respectively. Therefore, summer
rainfall can be predicted using the equation: summer rainfall = 286.7839 -1.42435*growing
season rainfall + 96.63933 *wheat yield. Moreover, the correlation coefficient and the coefficient
of determination of growing season rainfall and wheat yield are 0.735602 and 0.541111,
respectively. Also, the observed p-value for the fitted regression model is 0.006326 at 5%
significance value. The corresponding p-values for individual variables (growing season rainfall
and wheat yield) are 0.017325 and 0.00238, respectively.
Interpretation
Since the correlation coefficient between the explanatory and response variable is 0.7356,
then there exists a 73.56% linear relation between wheat yield, summer, and growing season
rainfall. Additionally, the model explains 54.11% sample variation of the summer rainfall by
growing season rainfall and wheat yield. Generally, the fitted regression model is statistically
significant at a 5% significance value since the observed p-value (0.006) is less than 0.05. Also,
the independent variables summer and growing season rainfall are statistically independent since
their corresponding p-values are less than 0.05 at 5% significance level.
Conclusion
The amount of rainfall for season growing and wheat yield affect summer rainfall
significantly. Moreover, the fitted regression model predicts summer rainfall sufficiently.

MULTIPLE REGRESSION ANALYSIS 4
Reference
Davies, A. (2017) Understanding Statistics : An Introduction. Washington,
D.C.:Libertarianism.org Press. Available at:http://search.ebscohost.com/login.aspx?
direct=true&db=nlebk&AN=1667844&site=eds-live (Accessed: 17 July 2019