Short Title: Kaplan-Meier Survival Analysis

The provided content consists of a hypothetical cohort of 10 persons followed for up to 24 months after treatment between January 2004 and January 2006. The data includes information on death, censored observations, and time-to-death from treatment (in months). The assignment requires the calculation of the 2-year cumulative probability of death using both Kaplan-Meier and life table methods.

Name Gomez, Andrew
Homework 2: Measures of occurrence and morality, Kaplan Meier (Epi I, fall 2017)
Please show your work! Please email to [e-mail] and [e-mail] by
Monday 9/11 by 11am CT.
The risk is a proportion, not a rate. Proportions do not have any units (or at least, the units
cancel out, as in “4 out of 5 dentists prefer Trident gum”. Rates always have time in the
denominator, as in “55 miles per hour.”
Risk is the number of people who develop disease, divided by the number of people “at risk” of
that disease over a period of time. More exactly, cumulative incidence is a measure of risk. You
can think of it as a percentage (proportion per 100 people), but sometimes it is too rare for
percentage to be useful; in this case it might be the number of cases per 100,000 or per million.
People are “at risk” if they can develop the disease. For example, men are not at risk for
ovarian cancer, because they lack ovaries (however, men are at risk for breast cancer, because
men do have breasts; it just isn’t as common). Usually, our goal is just to calculate the risk, but
to compare risk in two groups: those exposed to some risk factor, and those not exposed.
In this 2x2 table, we put the disease status or mortality along the top (columns), and the
exposure status or risk factor along the side (rows). In this simple case, we’ll use a classic
example: smoking and lung cancer. As in the Wickham study (from Rothman’s Epidemiology:
An Introduction), there were 20 years of follow-up between smoking assessment and the end of
the study; subjects could develop lung cancer at any point over the followup period.
Developed
lung cancer
Didn’t develop
lung cancer
Total number
“at risk” of lung
cancer
Person smoked 750 4,250 5,000
Person did not
smoke
250 9,750 10,000
Total 1,000 14,000 15,000
Answer the following 4 questions related to this hypothetical study.
1. What is the proportion of smokers in the population (at the beginning of the study)? That is,
what percentage smokes?
Solution
Proportion of Smokers= No . of Smokers
Total Population = 5000
15000∗100 %=33.33 %
2. What proportion of the total population develops lung cancer (over the 20 years of follow-
up)?
Solution

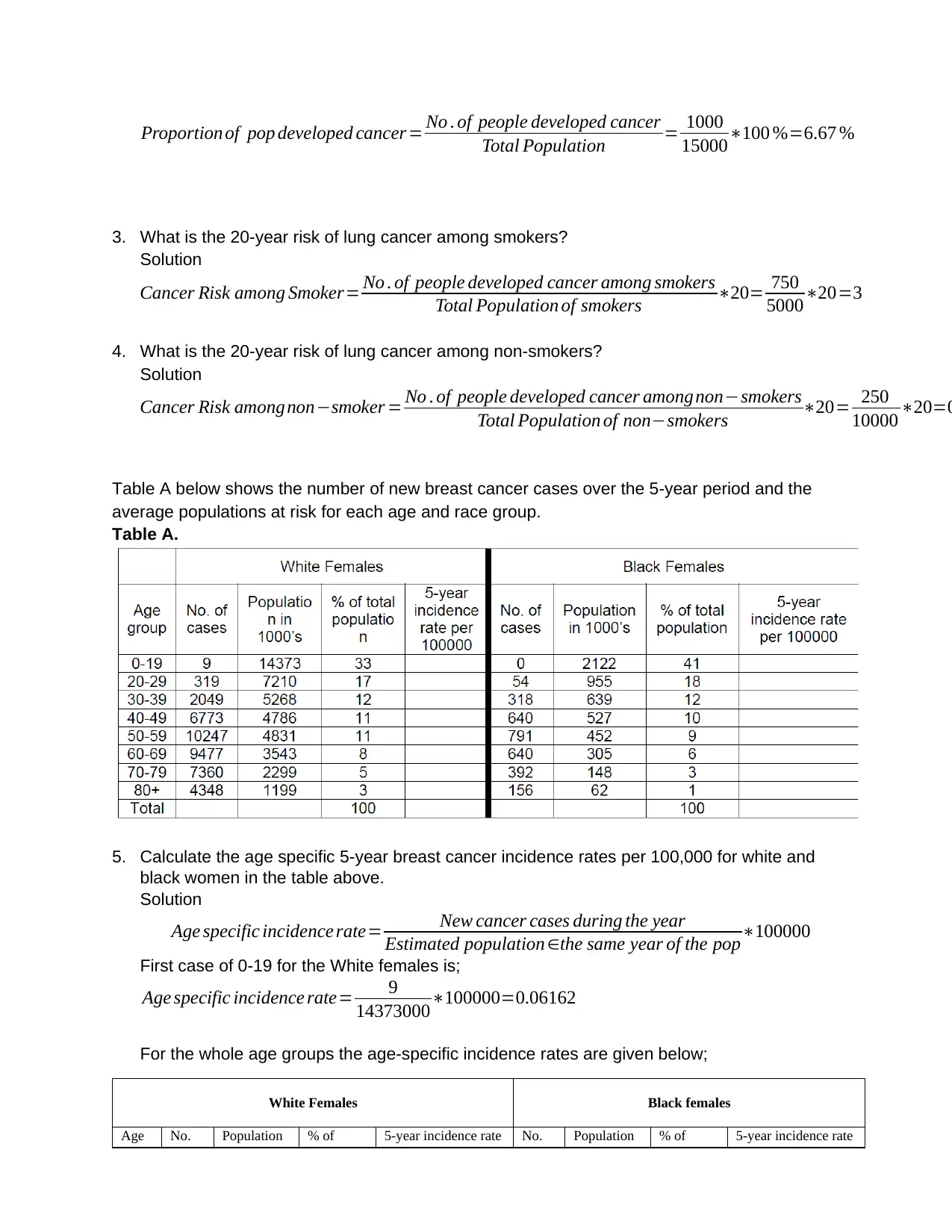
Proportion of pop developed cancer = No . of people developed cancer
Total Population = 1000
15000∗100 %=6.67 %
3. What is the 20-year risk of lung cancer among smokers?
Solution
Cancer Risk among Smoker= No . of people developed cancer among smokers
Total Population of smokers ∗20= 750
5000∗20=3
4. What is the 20-year risk of lung cancer among non-smokers?
Solution
Cancer Risk among non−smoker = No . of people developed cancer amongnon−smokers
Total Population of non−smokers ∗20= 250
10000 ∗20=0
Table A below shows the number of new breast cancer cases over the 5-year period and the
average populations at risk for each age and race group.
Table A.
5. Calculate the age specific 5-year breast cancer incidence rates per 100,000 for white and
black women in the table above.
Solution
Age specific incidence rate= New cancer cases during the year
Estimated population ∈the same year of the pop∗100000
First case of 0-19 for the White females is;
Age specific incidence rate= 9
14373000∗100000=0.06162
For the whole age groups the age-specific incidence rates are given below;
White Females Black females
Age No. Population % of 5-year incidence rate No. Population % of 5-year incidence rate

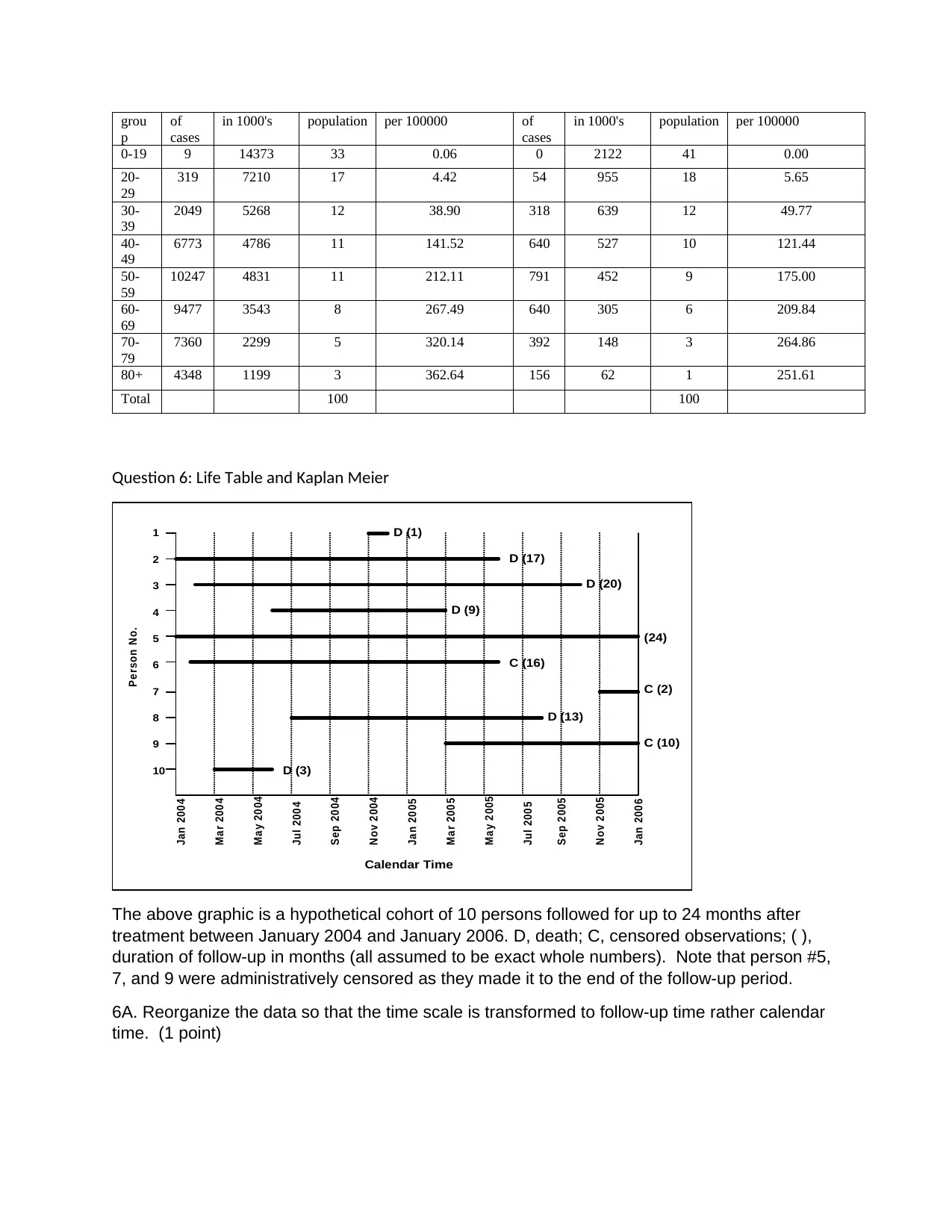
grou
p
of
cases
in 1000's population per 100000 of
cases
in 1000's population per 100000
0-19 9 14373 33 0.06 0 2122 41 0.00
20-
29
319 7210 17 4.42 54 955 18 5.65
30-
39
2049 5268 12 38.90 318 639 12 49.77
40-
49
6773 4786 11 141.52 640 527 10 121.44
50-
59
10247 4831 11 212.11 791 452 9 175.00
60-
69
9477 3543 8 267.49 640 305 6 209.84
70-
79
7360 2299 5 320.14 392 148 3 264.86
80+ 4348 1199 3 362.64 156 62 1 251.61
Total 100 100
Question 6: Life Table and Kaplan Meier
Person No.
1
2
3
4
5
6
7
8
9
10
Jan 2004
Mar 2004
May 2004
Jul 2004
Sep 2004
Nov 2004
Jan 2005
Mar 2005
May 2005
Jul 2005
Sep 2005
Nov 2005
Jan 2006
Calendar Time
D (1)
D (17)
D (20)
D (9)
C (16)
C (2)
C (10)
(24)
D (13)
D (3)
The above graphic is a hypothetical cohort of 10 persons followed for up to 24 months after
treatment between January 2004 and January 2006. D, death; C, censored observations; ( ),
duration of follow-up in months (all assumed to be exact whole numbers). Note that person #5,
7, and 9 were administratively censored as they made it to the end of the follow-up period.
6A. Reorganize the data so that the time scale is transformed to follow-up time rather calendar
time. (1 point)

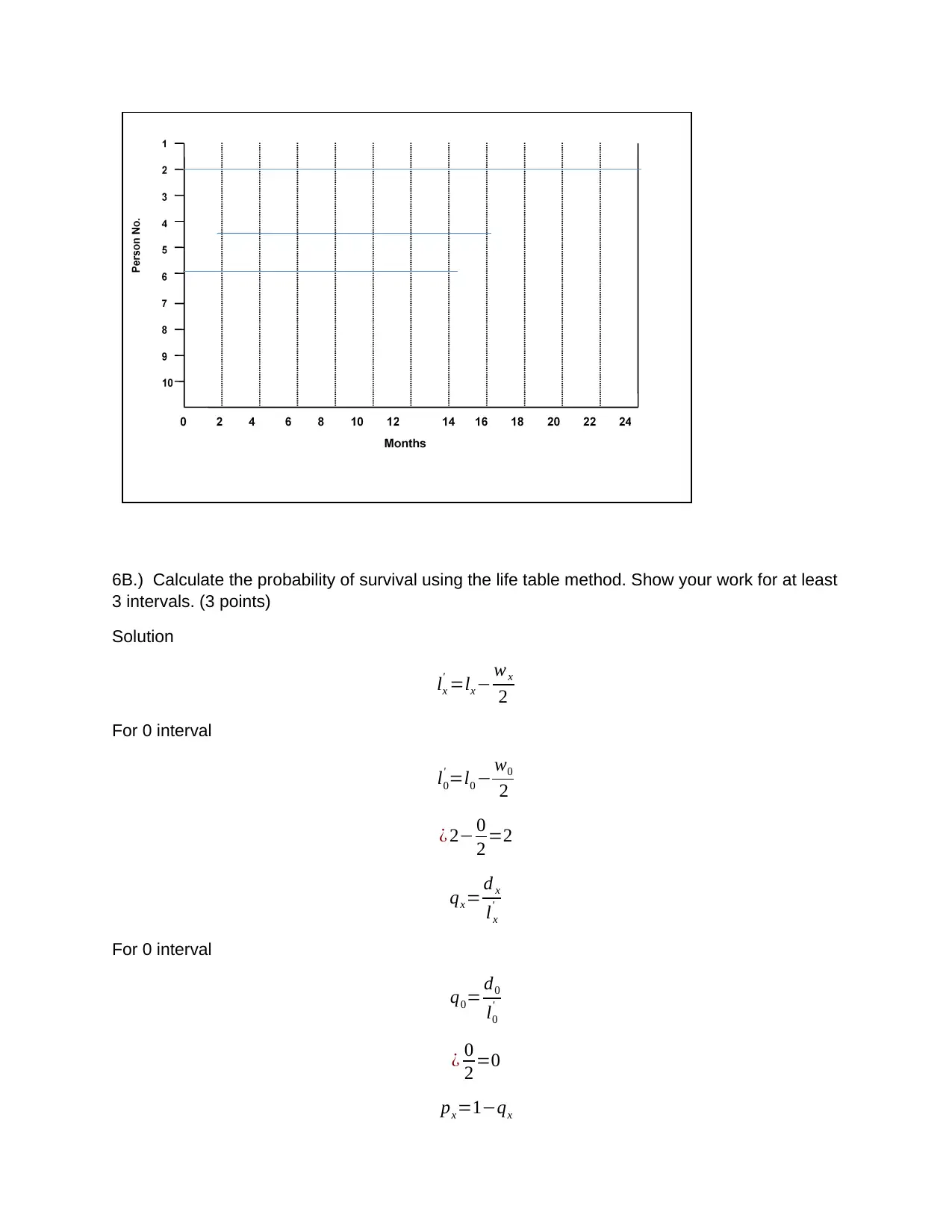
6B.) Calculate the probability of survival using the life table method. Show your work for at least
3 intervals. (3 points)
Solution
lx
' =lx− wx
2
For 0 interval
l0
' =l0 − w0
2
¿ 2− 0
2 =2
qx= d x
lx
'
For 0 interval
q0= d0
l0
'
¿ 0
2 =0
px=1−qx

For 0 interval
p0=1−q0
¿ 1−0=1
(1)
Interval
Since
Beginning
Treatment
(2)
Alive at
Beginning
of Interval
(3)
Endpoint
(Death)
Occurred
During
Interval
(4)
Censored
(5)
Adjusted
Number
at Risk:
Number
Exposed
to Risk of
Dying
(6)
Proportion
Who Died
During
Interval
(7)
Proportion
Who Did
Not Die
During
Interval
(8)
Cumulative
Proportion
Who
Survived
From
Enrollment
to End of
Interval
Cum.
Survival
x Ix dx wx I' x qx px Px
0 2 0 0 2 0.0000 1.0000 1.0000
2 5 0 0 5 0.0000 1.0000 1.0000
4 5 0 0 5 0.0000 1.0000 1.0000
6 6 1 0 6 0.1667 0.8333 1.0000
8 6 0 0 6 0.0000 1.0000 0.8333
10 7 0 0 7 0.0000 1.0000 0.8333
12 6 1 0 6 0.3333 0.6667 0.8333
14 6 1 0 6 0.3333 0.6667 0.5556
16 6 0 0 6 0.0000 1.0000 0.3704
18 4 1 1 3.5 0.2857 0.7143 0.3704
20 3 1 0 3.0 0.3333 0.6667 0.2646
22 3 1 0 3.0 0.3333 0.6667 0.1764
24 3 0 3 1.5 0.0000 1.0000 0.1176
6C.) What is the 2-year cumulative probability of death (event)? Show your calculation. (1 point)
Solution
Cumulative probability at time 0 is P(0)=1
Cumulative probability at time 1 is P(1)= p0 * P0
In our case is P(1)=1*1 = 1
2-year cumulative probability is;
P(24)= p22 * P22
P(24)= 0.6667*0.1764=0.1176

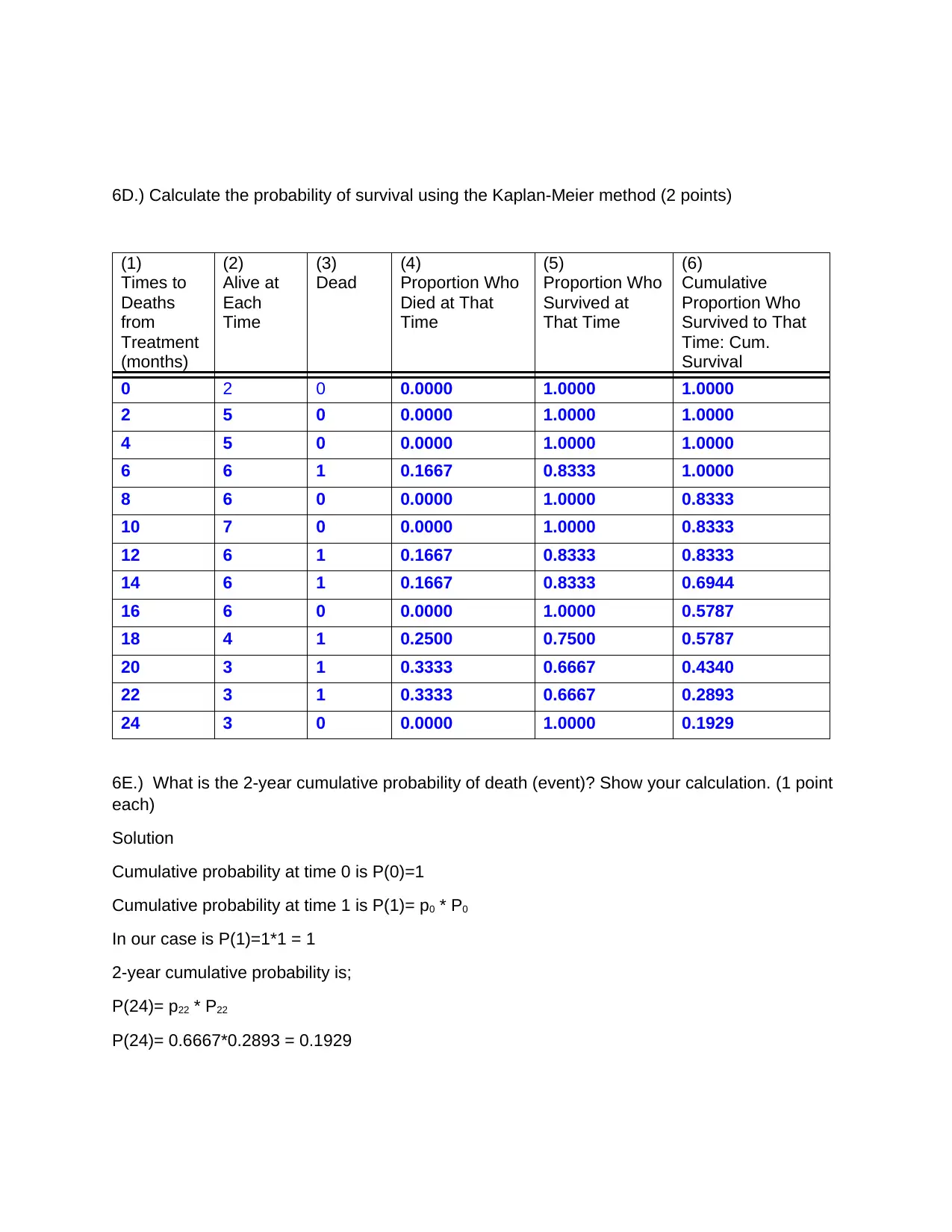
6D.) Calculate the probability of survival using the Kaplan-Meier method (2 points)
(1)
Times to
Deaths
from
Treatment
(months)
(2)
Alive at
Each
Time
(3)
Dead
(4)
Proportion Who
Died at That
Time
(5)
Proportion Who
Survived at
That Time
(6)
Cumulative
Proportion Who
Survived to That
Time: Cum.
Survival
0 2 0 0.0000 1.0000 1.0000
2 5 0 0.0000 1.0000 1.0000
4 5 0 0.0000 1.0000 1.0000
6 6 1 0.1667 0.8333 1.0000
8 6 0 0.0000 1.0000 0.8333
10 7 0 0.0000 1.0000 0.8333
12 6 1 0.1667 0.8333 0.8333
14 6 1 0.1667 0.8333 0.6944
16 6 0 0.0000 1.0000 0.5787
18 4 1 0.2500 0.7500 0.5787
20 3 1 0.3333 0.6667 0.4340
22 3 1 0.3333 0.6667 0.2893
24 3 0 0.0000 1.0000 0.1929
6E.) What is the 2-year cumulative probability of death (event)? Show your calculation. (1 point
each)
Solution
Cumulative probability at time 0 is P(0)=1
Cumulative probability at time 1 is P(1)= p0 * P0
In our case is P(1)=1*1 = 1
2-year cumulative probability is;
P(24)= p22 * P22
P(24)= 0.6667*0.2893 = 0.1929