Solution: ENGIN2020 Vibration and Machine Dynamics Assignment 2

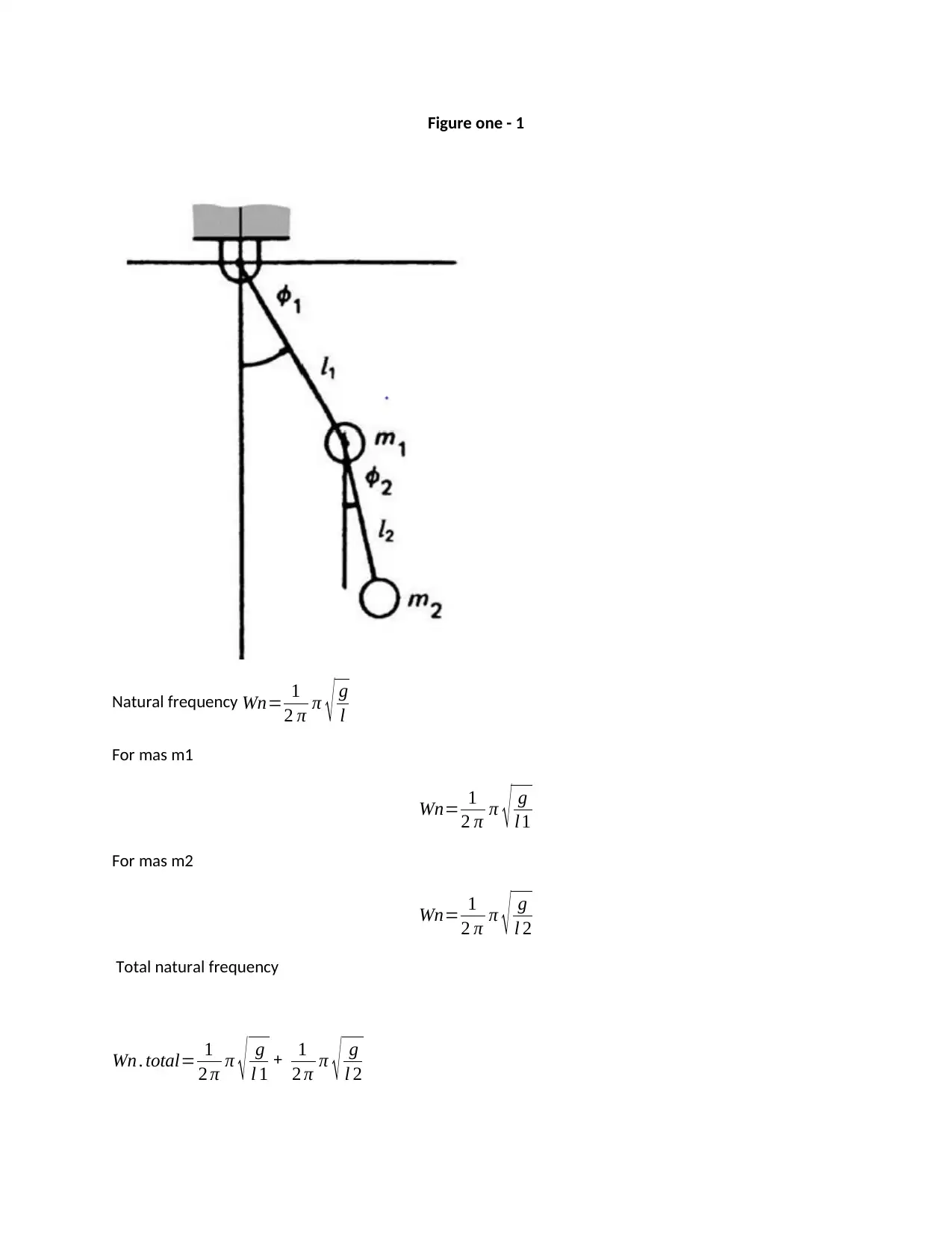
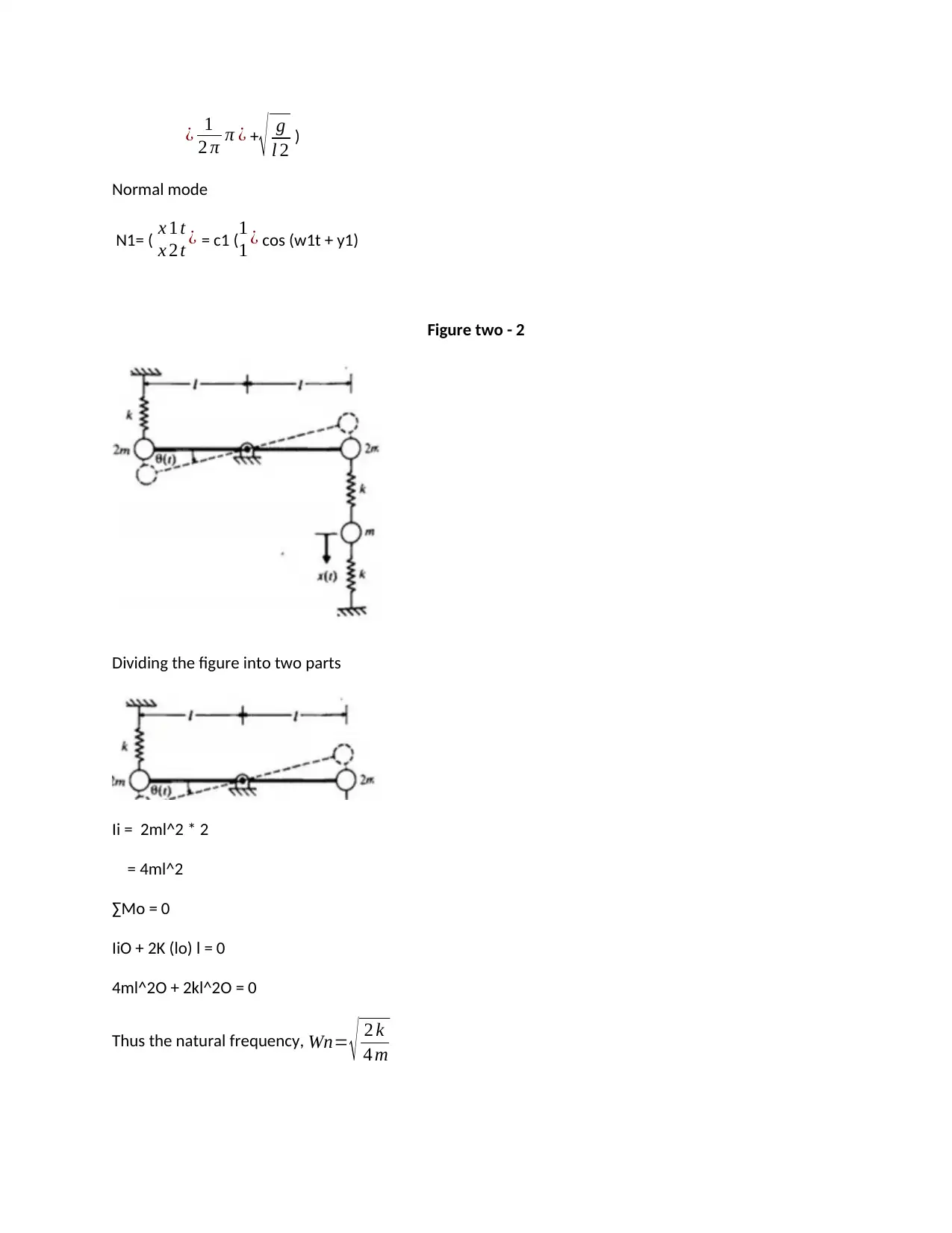
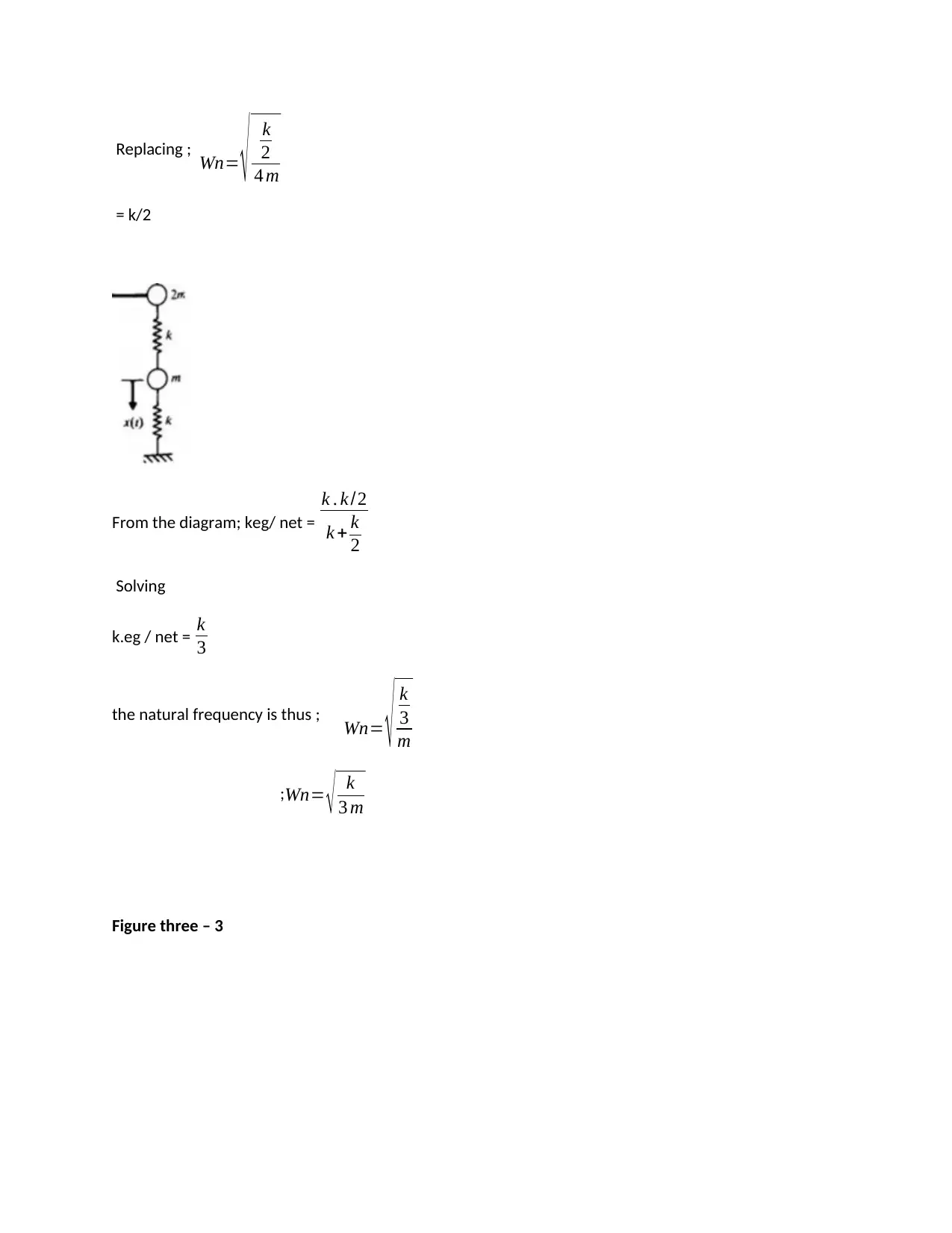
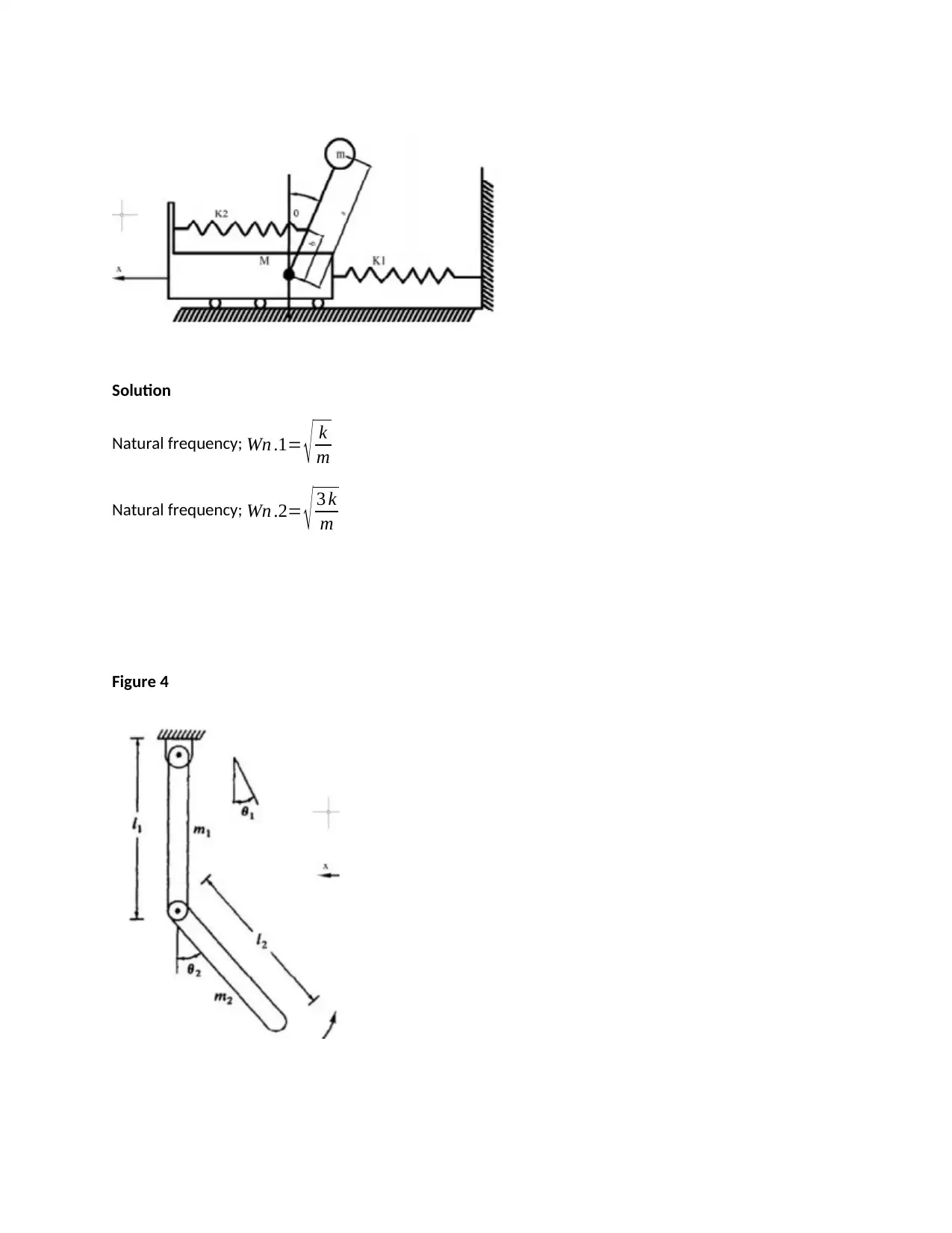
This assignment solution addresses a Vibration and Machine Dynamics problem set, focusing on two-degree-of-freedom vibration analysis. The solution determines natural frequencies and normal modes for various systems, including a system where the distance between two masses is constrained. It also analyzes a vehicle suspension system, calculating natural frequencies, normal modes, and vibration amplitudes under road excitation. The solution incorporates figures illustrating the systems and references relevant literature such as 'Vibration of Mechanical Systems' by Alok Sinha. The assignment covers concepts like mass matrix, damping matrix, and stiffness matrix, which are essential for understanding the dynamics of mechanical systems. The solution also provides a breakdown of the steps needed to solve the problems, including the application of formulas and diagrams to find the desired results.

Figure one - 1
Natural frequency Wn= 1
2 π π √ g
l
For mas m1
Wn= 1
2 π π √ g
l1
For mas m2
Wn= 1
2 π π √ g
l 2
Total natural frequency
Wn . total= 1
2 π π √ g
l 1 + 1
2 π π √ g
l 2

¿ 1
2 π π ¿ +
√ g
l 2 )
Normal mode
N1= ( x 1 t
x 2 t ¿ = c1 (1
1 ¿ cos (w1t + y1)
Figure two - 2
Dividing the figure into two parts
Ii = 2ml^2 * 2
= 4ml^2
∑Mo = 0
IiO + 2K (lo) l = 0
4ml^2O + 2kl^2O = 0
Thus the natural frequency, Wn= √ 2 k
4 m

Replacing ; Wn= √ k
2
4 m
= k/2
From the diagram; keg/ net =
k . k /2
k + k
2
Solving
k.eg / net = k
3
the natural frequency is thus ; Wn= √ k
3
m
;Wn= √ k
3 m
Figure three – 3

Solution
Natural frequency; Wn .1= √ k
m
Natural frequency; Wn .2= √ 3 k
m
Figure 4

Natural frequency Wn= 1
2 π π √ g
l
For mas m1
Wn= 1
2 π √ g
l 1
For mas m2
Wn= 1
2 π √ g
l 2
Natural frequency
Wn . total= 1
2 π π √ g
l 1 + 1
2 π π √ g
l 2
¿ 1
2 π π ¿ +
√ g
l 2 )
Figure 5
Solution
( A 11 A 12
A 21 A 22)- V 1 0
0 1 ( X 1
X 2 ¿=0
0

(
k 1
m
−k 2
m
−k 2
m
k 2
m + k 3
m
¿- w2
( 1 0
0 1 ) ( X 1
X 2 ¿=0
0
Solving out
ω1 = √ k
mand ω2 = √ 3 k
m

Work cited
Ahirrao, N. S., Bhosle, S. P., & Nehete, D. V. (2018). Dynamics and vibration measurements in
engines. Procedia Manufacturing, 20, 434-439.
Astashev, V., & Krupenin, V. (2017). Efficiency of vibration machines. Engineering for rural
development. Jelgava, 24(26.05).
Neyman, L. A., Neyman, V. Y., & Shabanov, A. S. (2017, June). Vibration dynamics of an
electromagnetic drive with a half-period rectifier. In 2017 18th International Conference
of Young Specialists on Micro/Nanotechnologies and Electron Devices (EDM) (pp. 503-
506). IEEE.