Network Optimization: Graph Theory Algorithms and Implementation
VerifiedAdded on 2023/06/08
|16
|1379
|79
Homework Assignment
AI Summary
This assignment focuses on network optimization using graph theory. It covers various concepts, including graph representation using linked lists, edge lists, and vertex deletion. The solution demonstrates the application of algorithms like Dijkstra's for finding the shortest path, Depth-First Search (DFS), Breadth-First Search (BFS), sequential coloring, and the Ford-Fulkerson algorithm for network flow. The assignment also delves into graph factorization and polynomial expressions related to graph properties. The goal is to illustrate how graph theory can be applied to model and optimize networks, with practical examples and detailed explanations provided for each question.

Network Optimisation
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Contents
1. Introduction..............................................................................................................................3
2. 2. Question 2.............................................................................................................................5
3. Question 3.................................................................................................................................7
4. Question 4.................................................................................................................................9
5. Question 5...............................................................................................................................10
6. Question 6...............................................................................................................................11
7. Question 7...............................................................................................................................15
8. Conclusion..............................................................................................................................16
1. Introduction..............................................................................................................................3
2. 2. Question 2.............................................................................................................................5
3. Question 3.................................................................................................................................7
4. Question 4.................................................................................................................................9
5. Question 5...............................................................................................................................10
6. Question 6...............................................................................................................................11
7. Question 7...............................................................................................................................15
8. Conclusion..............................................................................................................................16

1. Introduction
The main goal of this project Graph theory. The graph theory is used to mathematics study of the
graphs which are mathematics structure used to model pair wise relation between the graphs. A
graph in this context is made up of the using linked list data structure and using the different
types of algorithm in the used for the mathematical solutions. A graph is used to make up of
vertices, edges, nodes, or pointers which are connected by the graph. Graph theory is useful in
design integrated circuits for computer structure. The graph can be used to model many types of
relations and process in application real information system. Given the problem that can be
represented the as a graph with the set of nodes is connected by the edges. The nodes are usually
to representing the communication of the each edge.
Linked list structure
A linked list is the dynamic data structure is used to collection of nodes and edges of the each
element are a separate object of the data structure. Each elements (we will call is node) of a list is
comprising of two items the data is consider to the next node. The last node is considered to null.
The entry point into a linked list is called head of the list. The main advantage of the linked list
against an array is that it does not allow direct access to individual nodes element. If u wants to
access particular node then you have to start at the head node of the list. Linked list is used to
access to be consider the more memory allocation compare with array. A linked list is the
sequence of data structures which are connected together via links. The pointers are used to
objects that store the memory address of the value located in the list structure. A linked list is
used to connected of the node is used for the pointers. Unused linked list is used to order is not
given by the linked list.
The main goal of this project Graph theory. The graph theory is used to mathematics study of the
graphs which are mathematics structure used to model pair wise relation between the graphs. A
graph in this context is made up of the using linked list data structure and using the different
types of algorithm in the used for the mathematical solutions. A graph is used to make up of
vertices, edges, nodes, or pointers which are connected by the graph. Graph theory is useful in
design integrated circuits for computer structure. The graph can be used to model many types of
relations and process in application real information system. Given the problem that can be
represented the as a graph with the set of nodes is connected by the edges. The nodes are usually
to representing the communication of the each edge.
Linked list structure
A linked list is the dynamic data structure is used to collection of nodes and edges of the each
element are a separate object of the data structure. Each elements (we will call is node) of a list is
comprising of two items the data is consider to the next node. The last node is considered to null.
The entry point into a linked list is called head of the list. The main advantage of the linked list
against an array is that it does not allow direct access to individual nodes element. If u wants to
access particular node then you have to start at the head node of the list. Linked list is used to
access to be consider the more memory allocation compare with array. A linked list is the
sequence of data structures which are connected together via links. The pointers are used to
objects that store the memory address of the value located in the list structure. A linked list is
used to connected of the node is used for the pointers. Unused linked list is used to order is not
given by the linked list.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
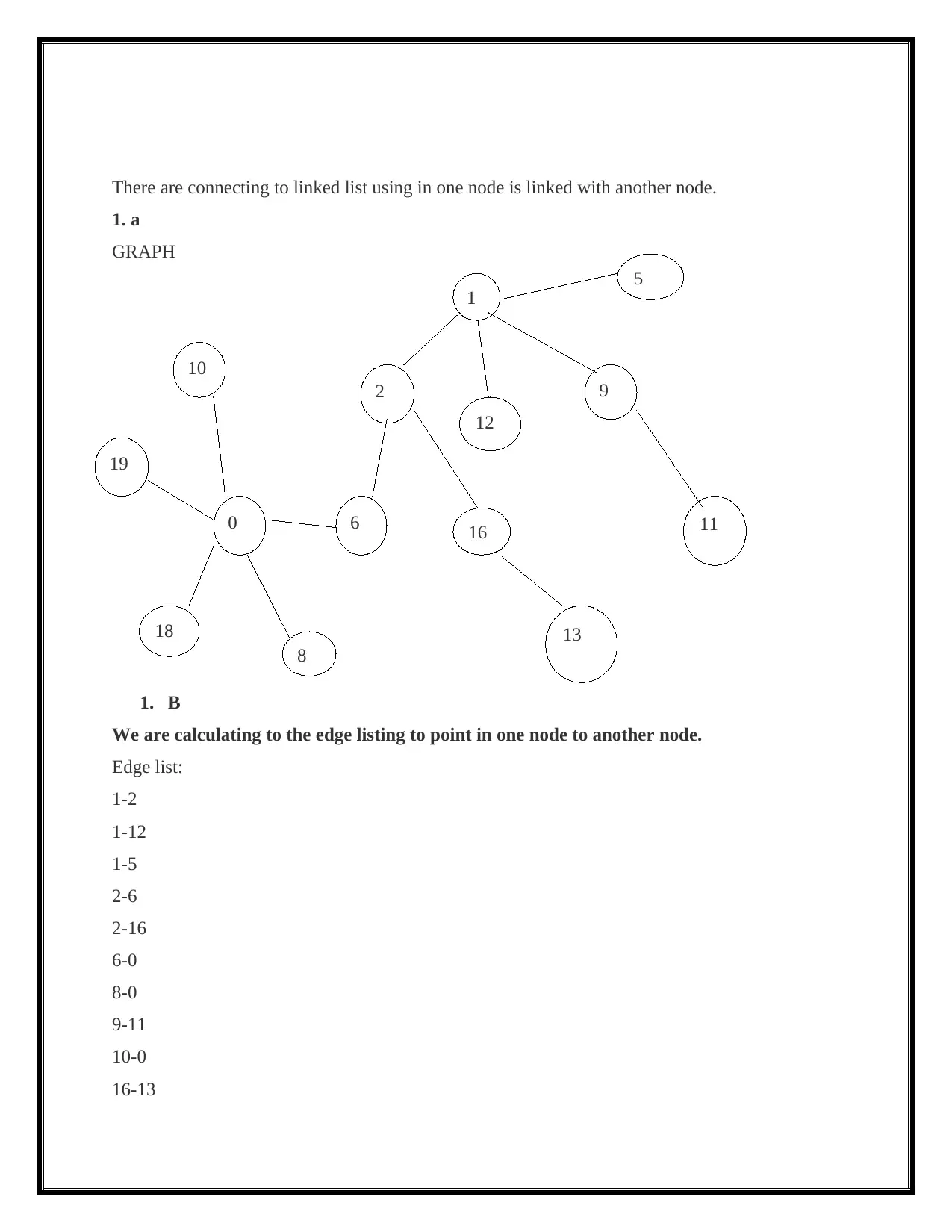
There are connecting to linked list using in one node is linked with another node.
1. a
GRAPH
9
1. B
We are calculating to the edge listing to point in one node to another node.
Edge list:
1-2
1-12
1-5
2-6
2-16
6-0
8-0
9-11
10-0
16-13
1
9
12
2
5
60
10
19
18
8
16
13
11
1. a
GRAPH
9
1. B
We are calculating to the edge listing to point in one node to another node.
Edge list:
1-2
1-12
1-5
2-6
2-16
6-0
8-0
9-11
10-0
16-13
1
9
12
2
5
60
10
19
18
8
16
13
11
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

18-0
19-0
1. c
We are calculating the delete vertex of v1 and v4 and remaining vertex in store in array of the
data structure.
Link list structure after delete vertex v1 and v4
2 3 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
2 - - - 3 5 - 5 3 - - - - 2 - 5 -
6 - 7 0 10 0 11 0 4 18 19 - - 13 - 0 0
2. 2. Question 2
2. A.
G is a connected graph of each vertex.
Let us consider to the n number of edges and n number of vertices.
The degree of vertices is written us d(V)is the number if number of edges with d(E) and the end
vertex.
𝑊 = 𝑣0𝑒1𝑣1𝑒2𝑣2 … 𝑒𝑛𝑣𝑛 graph of G
𝑐𝑎𝑝𝑎𝑐𝑖𝑡𝑦 (𝑊) = min{𝑤𝑒𝑖𝑔ℎ𝑡(𝑒𝑖 ):𝑖 = 1, … , 𝑛}
Pair of (u, v)
V (G) = (u, v)
𝑊 = 𝑣0𝑒1𝑣1𝑒2𝑣2 … 𝑒𝑛𝑣𝑛
Let us consider the v0=v1 fix a vertex of v€ v (G)
Let us appears in w as vi1….vi k, if v! =v0=v n then
W (li)=2k, if v=vo =vj =vi k=v n
With k>=2
W (ei) =2(k-1)
2. b. The problem to finding the shortest path form source vertex v to all other vertices
in the graph using shortest dijkstra’s algorithm.
19-0
1. c
We are calculating the delete vertex of v1 and v4 and remaining vertex in store in array of the
data structure.
Link list structure after delete vertex v1 and v4
2 3 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
2 - - - 3 5 - 5 3 - - - - 2 - 5 -
6 - 7 0 10 0 11 0 4 18 19 - - 13 - 0 0
2. 2. Question 2
2. A.
G is a connected graph of each vertex.
Let us consider to the n number of edges and n number of vertices.
The degree of vertices is written us d(V)is the number if number of edges with d(E) and the end
vertex.
𝑊 = 𝑣0𝑒1𝑣1𝑒2𝑣2 … 𝑒𝑛𝑣𝑛 graph of G
𝑐𝑎𝑝𝑎𝑐𝑖𝑡𝑦 (𝑊) = min{𝑤𝑒𝑖𝑔ℎ𝑡(𝑒𝑖 ):𝑖 = 1, … , 𝑛}
Pair of (u, v)
V (G) = (u, v)
𝑊 = 𝑣0𝑒1𝑣1𝑒2𝑣2 … 𝑒𝑛𝑣𝑛
Let us consider the v0=v1 fix a vertex of v€ v (G)
Let us appears in w as vi1….vi k, if v! =v0=v n then
W (li)=2k, if v=vo =vj =vi k=v n
With k>=2
W (ei) =2(k-1)
2. b. The problem to finding the shortest path form source vertex v to all other vertices
in the graph using shortest dijkstra’s algorithm.
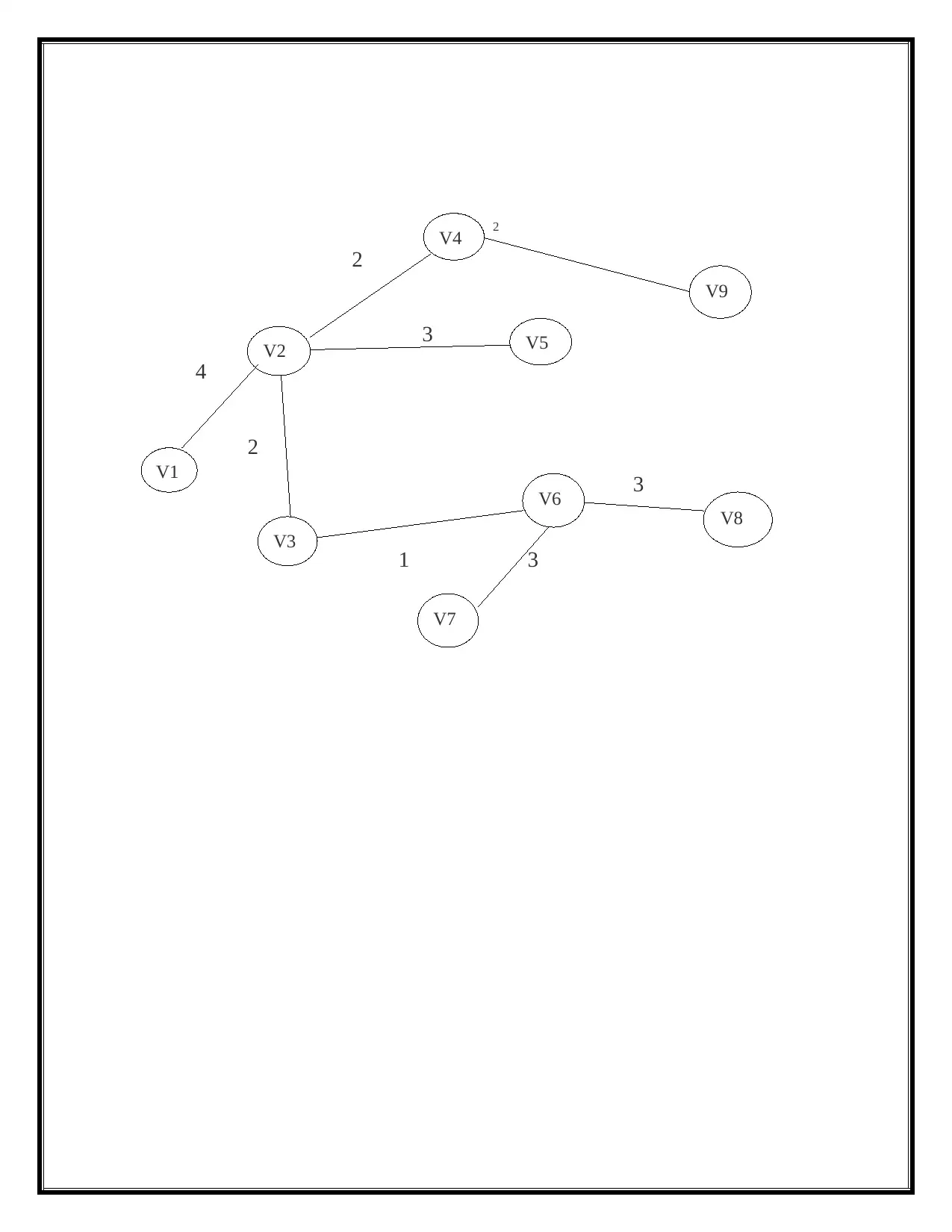
2
2
3
4
2
3
1 3
V1
V2
V3
V7
V6
V5
V4
V8
V9
2
3
4
2
3
1 3
V1
V2
V3
V7
V6
V5
V4
V8
V9
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

3. Question 3
DFS
The Depth first search algorithm using starting vertex v1.pick the starting node of
v1 and push its entire adjacent node in the data structure. Pop a node from stack to
select the next node to visit the push all its adjacent nodes. And ending nodes of
v11. We are finding the maximum capacity of the vertices.
V5
V2 V9
V6
V1 V4
V7 V3
V10
V11
V8
V12
DFS
The Depth first search algorithm using starting vertex v1.pick the starting node of
v1 and push its entire adjacent node in the data structure. Pop a node from stack to
select the next node to visit the push all its adjacent nodes. And ending nodes of
v11. We are finding the maximum capacity of the vertices.
V5
V2 V9
V6
V1 V4
V7 V3
V10
V11
V8
V12
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
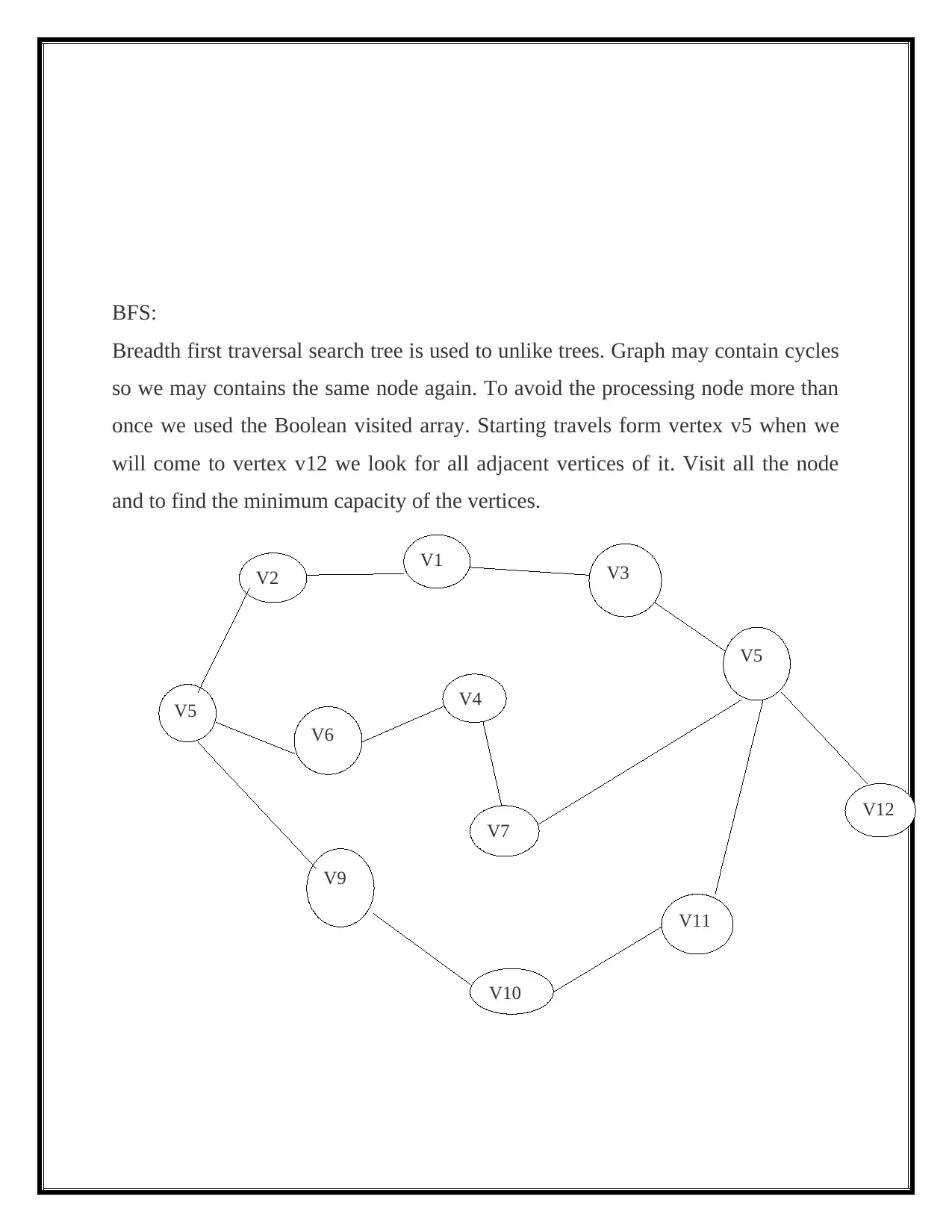
BFS:
Breadth first traversal search tree is used to unlike trees. Graph may contain cycles
so we may contains the same node again. To avoid the processing node more than
once we used the Boolean visited array. Starting travels form vertex v5 when we
will come to vertex v12 we look for all adjacent vertices of it. Visit all the node
and to find the minimum capacity of the vertices.
V5
V2
V6
V9
V1
V4
V7
V10
V3
V5
V12
V11
Breadth first traversal search tree is used to unlike trees. Graph may contain cycles
so we may contains the same node again. To avoid the processing node more than
once we used the Boolean visited array. Starting travels form vertex v5 when we
will come to vertex v12 we look for all adjacent vertices of it. Visit all the node
and to find the minimum capacity of the vertices.
V5
V2
V6
V9
V1
V4
V7
V10
V3
V5
V12
V11

4. Question 4
The sequential coloring algorithm is used to visit the all edges and vertices to find the maximum
of the edges to mention the color the edges. The each edges visit at single time. To find the
coloring edges.
The sequential coloring algorithm is used to visit the all edges and vertices to find the maximum
of the edges to mention the color the edges. The each edges visit at single time. To find the
coloring edges.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

5. Question 5
5. a (a) 6 - 9 5 + 8 4 - 6 3 + 2 + 2 (b) 9 - 25 8 + 40 7 - 40 6 + 30 5 - 20 4 + 5
3
Polynomial used to find the expression consisting of the variable and that involves addition,
subtraction, multiplication and the non negative integer exponents of variables. If the valid
equation is correct is the polynomial.
Its polynomial
5. a (a) 6 - 9 5 + 8 4 - 6 3 + 2 + 2 (b) 9 - 25 8 + 40 7 - 40 6 + 30 5 - 20 4 + 5
3
Polynomial used to find the expression consisting of the variable and that involves addition,
subtraction, multiplication and the non negative integer exponents of variables. If the valid
equation is correct is the polynomial.
Its polynomial
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

5. B
Its polynomial
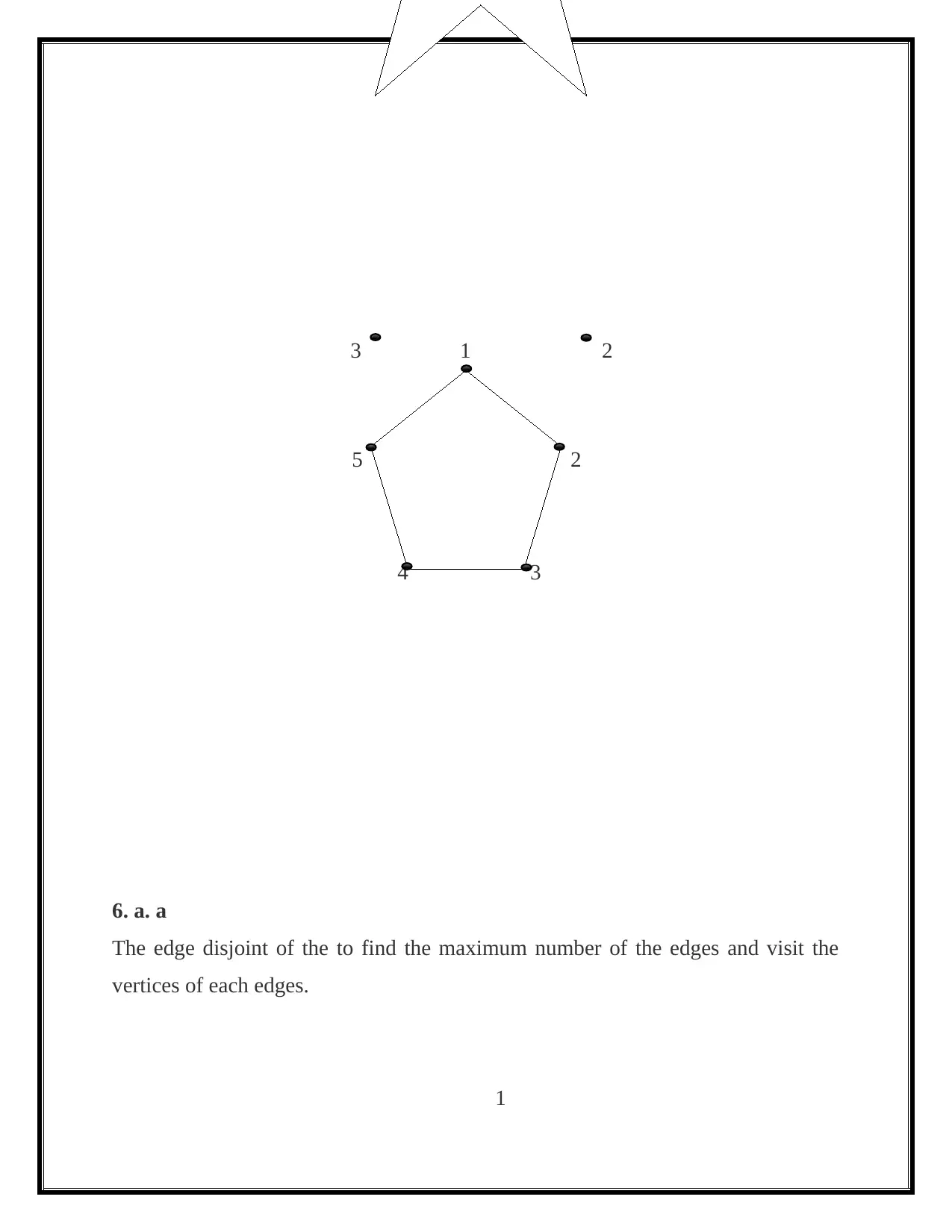
6. Question 6
Graph 2 factorable. The connected graph of the G is a regular graph and have
even number of vertices.
5
4 1
Its polynomial
6. Question 6
Graph 2 factorable. The connected graph of the G is a regular graph and have
even number of vertices.
5
4 1
3 1 2
5 2
4 3
6. a. a
The edge disjoint of the to find the maximum number of the edges and visit the
vertices of each edges.
1
5 2
4 3
6. a. a
The edge disjoint of the to find the maximum number of the edges and visit the
vertices of each edges.
1
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 16
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





