Detailed Review: Chaney's Network Structure of International Trade

This paper reviews Thomas Chaney's 'The Network Structure of International Trade,' published in the American Economic Review in 2014. The study introduces a novel theory of trade frictions, emphasizing the role of informational networks in international trade. Motivated by empirical evidence from French firms' exports, Chaney proposes that firms export only to markets where they have a contact, searching directly and remotely for new trading partners through their existing network. The model characterizes the dynamic formation of an international exporter network and is structurally estimated using French data, confirming predictions about the distribution of foreign markets accessed and the geographic distribution of exports. The review highlights the paper's contributions, including the introduction of informational frictions, a dynamic model of trade frictions, and the explicit accounting for the geography of trade. It also relates the paper to existing literature on international trade, networks, and the role of trade intermediaries.

American Economic Review 2014, 104(11): 3600–3634
http://dx.doi.org/10.1257/aer.104.11.3600
3600
The Network Structure of International Trade†
By Thomas Chaney *
Motivated by empirical evidence I uncover on the dynamics of
French firms’ exports, I offer a novel theory of trade frictions. Firms
export only into markets where they have a contact. They search
directly for new trading partners, but also use their existing network
of contacts to search remotely for new partners. I characterize the
dynamic formation of an international network of exporters in this
model. Structurally, I estimate this model on French data and confirm
its predictions regarding the distribution of the number of foreign
markets accessed by exporters and the geographic distribution of
exports. (JEL D85, F11, F14, L24)
This paper proposes a new theory of the frictions associated with internationa
trade, and more generally the frictions that affect the ability of firms to trade w
each other. Samuelson (1954) and later Krugman (1980) recognized the key im
tance that trade frictions play not only in shaping the patterns of international
but also in determining relative factor prices between countries, and ulti
comparative development. Despite the central role they play in trade models, t
frictions remain largely unexplained, and we only have a very crude formalizat
of those frictions. Samuelson (1954), Krugman (1980) and most of the trade lit
ture assume “iceberg”-type trade costs, a simple proportional cost. Melitz (200
Helpman, Melitz, and Rubinstein (2008); and Chaney (2008) recognize the imp
tance of the extensive margin of trade in determining firm level and aggregate
and introduce a fixed cost in addition to the usual iceberg cost. Arkolakis (2010
further endogenizes this fixed cost and allows firms to choose from a menu of fi
costs. Yet this simple combination of a fixed and a variable cost is too crude to
ture many facts about firm-level exports. Whereas Bernard et al. (2003) or Mel
(2003) assume that differences in the ability of firms to enter foreign markets a
entirely driven by heterogeneous productivities, Armenter and Koren (forth
ing) point out that productivity differences can only account for a fraction of th
* Toulouse School of Economics, 21 Allee de Brienne, 31000 Toulouse, France (e-mail: thomas.chaney@gm
com). I am grateful to Enghin Atalay, Sylvain Chassang, Xavier Gabaix, Sam Kortum, Pierre-Louis Lions, Bob
Lucas, Marc Melitz, Roger Myerson, David Sraer, Nancy Stokey, and seminar participants at Chicago (Math a
Econ), Columbia, Harvard, MIT, the NBER Summer Institute, NYU, Princeton, Sciences Po (Paris), Toronto, the
Toulouse School of Economics, UBC Vancouver, UQAM, UW Milwaukee, Wharton, and Yale for helpful discus-
sions, and NSF grant SES-1061622 for financial support. I am indebted to Ferdinando Monte and Enghin Atal
for their superb research assistance. I declare that I have received in the last three years more than US$10,0
the National Science Foundation, in the form of a research grant (SES-1061622) for the particular research t
addressed in this paper. Beyond this grant, I have no relevant or material financial interests that relate to th
in this paper. First draft: July 2010.
† Go to http://dx.doi.org/10.1257/aer.104.11.3600 to visit the article page for additional materials and aut
disclosure statement(s).

3601CHANEY: THE NETWORK STRUCTURE OF TRADEVOL. 104 NO. 11
exposure to international markets. Similarly, Eaton, Kortum, and Kramarz (201
show that a large amount of idiosyncratic noise has to be added to the simple c
nation of fixed and variable costs of the Melitz model in order to empirically ma
firm level exports from France.
The main contribution of this paper is to develop a theory of trade frictions ba
on the notion of informational frictions. This theory is motivated by new stylize
facts I uncover on the dynamics of firm-level exports in France. The second con
bution of this paper is to build a dynamic model of trade frictions. While there a
strong patterns in the dynamics of firm-level trade, most existing trade models
static in essence.1 By adding structure to the export dynamics, I generate predictio
linking the cross section and the time series of international trade. The third co
bution of this paper is explicitly to account for the geography of trade. Geograp
measured as the physical distance between countries, plays a crucial role in ex
ing the empirical patterns of international trade, yet it is absent from most trad
models.2 I show how to introduce geographic space into a theoretical model of fi
level trade, and provide precise empirical evidence in support of the model. I fo
primarily on the physical distance between locations. The reason is both that th
a measure that is easy to calculate and that this is the measure that is empiric
most relevant to explain trade flows. Putting together those three contributions
notion that information is a key friction to trade, its corollary that the diffusion
information will follow an intrinsically dynamic process, and the fact that geogr
phy matters for trade in a specific way—this paper offers a very different persp
on international trade compared to traditional models.
Before describing the related literature, I will spell out quickly the main intuit
from the model, as well as the main predictions that I bring to the data.
Potential exporters meet foreign trading partners in two distinct ways.
firm searches directly for foreign partners, which I model as a geographically b
random search. Second, once a firm has acquired a network of foreign contacts
various foreign locations, it can search remotely for new trading partners from
locations. Those two assumptions are motivated by novel empirical evidence o
dynamics of firms exports I uncover using data on French firms from 1986 to 1
The more countries a firm exports to, the more likely it is to enter new market
sequently. Moreover, where a firm exports to affects which specific markets it w
enter in the future: if a French firm exports to country a in year t, it is then mor
likely to enter in year t + 1 a country b geographically close to a, even if b is no
close to France. The possibility to use existing contacts to find new ones gives
advantage to firms with many contacts. This generates a fat-tailed distribution
the number of foreign contacts across firms. The empirical distribution of the n
ber of foreign contacts is well described by the theory.
A more elaborate contribution of this paper accounts for geographic sp
Remote search allows say a French exporter that has a acquired a contact in Ja
1Dixit (1989); Krugman (1987); and Young (1991) are among a few early and notable exceptions, as are a
recent papers mentioned below in this introduction.
2There are a few important exceptions in the economic geography literature (for instance, Fujita, Krugman
Mori 1999). However, this literature is primarily theoretical, and rarely goes beyond testing a few stylized em
facts, if any. Desmet and Rossi-Hansberg (2010) identify some of the challenges of introducing space in an e
rium model, and show some empirical evidence. See Allen and Arkolakis (forthcoming) for a recent contribu

3602 THE AMERICAN ECONOMIC REVIEW NOVEMBER 2014
to radiate away from Japan as Japanese firms would. It does so by using its Japa
contacts as a remote hub from which it can expand out of Japan. By acquiring m
foreign contacts, firms expand into more remote countries and, as a result, exp
over longer distances. Empirically, the geographic distance of exports increase
the number of foreign contacts as the theory predicts.
This is a theory of a network. Therefore, a shock that hits anywhere will be
transmitted throughout the network, with an intensity that depends on the stru
ture of the network. The data confirms this prediction. For instance, I show that
a French firm which already exports to a, the probability that it begins exportin
to b will be higher following an increase in the trade volume between a and b,
else equal.
This paper contributes to the literature on international trade and networks.
There is a nascent literature in international trade and macroeconomics on th
that informational barriers and informational networks play in facilitating or ham
pering transactions, and in transmitting shocks. In a seminal paper, Rauch (199
conjectures that informational barriers play an important role. He offers a class
cation of traded goods between differentiated and homogeneous goods, and sh
that geographic proximity is more important for trade in differentiated goods. H
argues that this is evidence for the importance of informational barriers. While
Rauch classification has been used widely in international trade, the noti
informational networks are important in overcoming informational barriers
remained relatively underexplored. I offer a formal treatment of the network th
allows information to diffuse, and show evidence of this network using firm-leve
trade data. Rauch and Trindade (2002) show that the presence of ethnic Chine
networks facilitates bilateral trade, and particularly so for trade in differe
goods. They argue that these findings are evidence for the importance o
mational barriers, and that social networks mitigate those barriers. Rauch (200
offers a survey of the literature on networks in international trade. In the conte
intranational trade, Combes, Lafourcade, and Mayer (2005) show that social an
business networks facilitate trade between regions within France, where they u
migrations and multiplant firms to infer a measure of social and business linka
Using Spanish data, Garmendia et al. (2012) show that social and business net
have a stronger impact on the extensive margin than on the intensive margin o
a prediction that holds in my model. Burchardi and Hassan (2013) show that W
German regions which have closer social ties with East Germany inherited from
tumultuous history of refugees relocations after WWII experienced faster growt
and engaged in more investment into East Germany after the German reunifica
In this paper, I develop a more general model of the formation of an internation
network of firms, and show how this network matters for firm-level trade patter
over and beyond the effects analyzed in special cases studied so far.
On a somewhat related topic, Hidalgo et al. (2007) show that the product mix
goods manufactured and exported by countries can be described as a network
that countries move toward more connected sectors as they grow. Acemoglu e
(2012) describe the input-output linkages between sectors in the United States
network, and show how idiosyncratic shocks to individual sectors have a nonne
ble impact on aggregate volatility. The results I present on the transmission of
gate trade shocks on firm exports suggest that similar forces may be at play in

3603CHANEY: THE NETWORK STRUCTURE OF TRADEVOL. 104 NO. 11
This paper is also related to a recent literature which emphasizes the role of
intermediaries in overcoming informational barriers. Casella and Rauch (2
offer a formal model of trade with informational barriers. They assume that the
are only two types of agents: some are perfectly informed about the quality of
eign goods, while the others are uniformed. The informed agents may chose to
as intermediaries for international trade. I offer a more nuanced model where fi
gradually learn about foreign markets, so that there is close to a continuum of
with a differential access to information about foreign markets. Antràs and Cos
(2011) develop a theoretical model of trade that relaxes the assumption of a ce
ized Walrasian market, and derive predictions for the welfare gains from trade
setting where trade is intermediated. Ahn, Khandelwal, and Wei (2011) demon
empirically the importance of trade intermediaries in facilitating trade, especia
for smaller exporters and for penetrating less accessible markets. I do not form
introduce trade intermediaries, but I stress the importance of informational bar
ers, and show how a network can partially overcome these barriers. The netwo
I describe can be thought of as a formal treatment of how intermediaries conne
importers and exporters.
This paper is complementary to models of international trade with heterogen
firms such as Bernard et al. (2003), Melitz (2003) and its extension in C
(2008). Those models assume that differences in the ability of individual firms
enter foreign markets are driven entirely by some exogenous productivity diffe
ences, and by the configuration of exogenous parameters which govern the ac
sibility of different foreign markets. These models replicate successfully a serie
stylized facts regarding the size distribution of individual firms in different mark
and the efficiency of firms entering different sets of countries, as shown by Eat
Kortum, and Kramarz (2011). While successful at explaining the intensive marg
of firm-level trade, these models are unable to match simultaneously the differ
stylized facts I uncover regarding the distribution of the number and the geogr
location of foreign markets entered by different firms. By contrast, the m
develop offers a parsimonious explanation for the extensive margin of trade at
firm level, but is mostly silent about the intensive margin of trade. In that sens
model is complementary to the existing models of trade with heterogeneous fir
This paper is also complementary to a recent literature on the dynamics of ex
or more generally expansion at the firm level. Albornoz et al. (2012) and Defev
Heid, and Larch (2010) both present simple models of learning about a firm’s p
tial in a foreign market. They show evidence of the sequential entry into foreign
markets of Argentine and Chinese exporters, respectively, meaning that w
firm already exports influences where it enters next. Morales, Sheu, and
(2013) use a moment inequality estimation procedure to estimate a similar mo
sequential export choice, and document that exports tend to be history depend
They stress the importance of what they call extended gravity, which is
that if a firm exports to a particular country, it is subsequently more likely to ex
to other similar countries. This corresponds to the notion of remote search in m
model. In the case study of a single firm, Jia (2008) and Holmes (2011) study th
geographic expansion of Wal-mart in the United States. Both stress the importa
of local complementarities. New Wal-mart outlets tend to benefit from the prox
ity of its existing retail centers. Local complementarities are similar to the notio

3604 THE AMERICAN ECONOMIC REVIEW NOVEMBER 2014
of remote search in my paper, and the expansion of this single firm is similar to
expansion of exporters in my model. My paper is complementary to those pape
the sense that I incorporate these observations formally into a theoretical mod
the dynamics of entry of firms. I show how to analyze the properties of this mo
a tractable way. And I show formally how the dynamics of firm-level exports sh
both the cross-sectional distribution of exports as well as the time series of exp
the firm level. By going further into solving a theoretical model, I extract empir
predictions which are easier to test.
Finally, this paper is indirectly related to the literature on social networks. Wh
there is no explicit notion of social ties in my model, the formal treatment of fir
linkages resembles the analysis of the social network literature. Jackson and Ro
(2007) propose a tractable way to combine the features of a random network a
a preferential network. The notions of direct and remote search in my model ar
similar to their notions of random and preferential attachment. The main theor
innovation of my model is to embed this general network into an arbitrary spac
For the purpose of this paper, I assume that this space corresponds to the phys
geographic space. It could alternatively correspond to any other space that des
some of the attributes of the agents connected through that network.3 Bramoulle
et al. (2012) consider a model with a finite number of types that are biased aga
each other. They show that over time, agents increase the diversity of their con
in the sense that they get connected with different types. They derive condition
under which an agent’s initial bias asymptotically vanishes. As the notion of a b
between types is similar to the notion of geographic distance between firms in
model, their results are comparable to the gradual geographic expansion of ex
in my model. The technique used in those papers for finitely many types is com
mentary to the approach for infinitely many types I use: while I can model a lar
number of types, I have to impose an assumption of symmetry that these auth
relax. Those more general assumptions however limit them to results with only
types, or to only monotonicity and asymptotic results with more than two types
I also offer an empirical application of a network model to a dataset much large
than has typically been used in the social network literature.
I present reduced-form evidence on the dynamics of firms exports in Section
build a theory motivated by this evidence in Section II, and structurally estimat
theory in Section III.
I. Reduced-Form Evidence on Trade Dynamics
In this section, I present reduced-form evidence that individual firms fo
history-dependent process when expanding into foreign markets. In partic
show that a firm which exports to more countries is more likely to enter new m
kets subsequently. More interestingly, where a firm currently exports affects w
new markets it enters subsequently: if a firm exports to country c′ at time t, it is
subsequently more likely to enter any country c that is closely connected to co
3See McPherson, Smith-Lovin, and Cook (2001) for an overview of various situations where agents tend to
nect to each other according to some attributes outside of the network, which is generally described as hom

3605CHANEY: THE NETWORK STRUCTURE OF TRADEVOL. 104 NO. 11
c′ , either in the sense that it is geographically close toc′ , or that it trades a lot with
c′ . This reduced-form evidence motivates the theory presented in the next sec
Data Sources.—I use two sources of data.4 First, I use firm-level export data for
French exporters, over the period 1986–1992. The data come from the same so
as the data used by Eaton, Kortum, and Kramarz (2011). For each firm and eac
year, I use information on the set of countries to which a firm exports. There ar
between 115,000 (in 1988) and 122,000 exporters (in 1987) in my sample (12
in 1992). Those firms export to a total of 103 different foreign countries for whi
I have additional information on size and location. French firms export on avera
to between 3.49 (in 1991) and 3.62 (in 1986) different foreign countries (3.50 i
1992).
In addition to these data on firm-level exports for France, I use information on
the size of countries, their distance from France and from each other, and aggr
bilateral trade between country pairs. The size of a country is measured as nom
gross domestic product (GDP), collected from the Penn World Tables. The dista
between two countries is the population-weighted geodesic distances between
main cities in both countries, collected from the CEPII. Finally, I use data on agg
gate bilateral trade flows between countries, collected from the NBER.
Regression Specification.—Formally, I estimate a Probit regression of differen
specifications of the following equation:
(1) Pr (exp or ti, c, t+1> 0 | observables)
= Φ
( α ∑c′
1[exp or ti,c′ , t > 0] + β1 g( Dis tFrance, c)
+ β2
∑ c′ 1[exp or ti,c′ , t > 0] g(Dis tc′ , c)
___
∑ c′ 1[exp or ti,c′ , t > 0]
+ β3
∑ c′ ≠Fr g( Dis tc′ , c)
__
Nc′ ≠France
+ γ1 ∑c′
Δ Export sc′ , c, t__
Export sc′ , c, t
+ γ2 ∑c′
1[exp or ti,c′ , t > 0] Δ Export sc′ , c, t__
Export sc′ , c, t
+ δ 1[exp or ti, c, t > 0] + Control sc,t) ,
where Φ is the c.d.f. of the standard normal distribution; 1[exp or ti, c, t+1> 0] takes
the value 1 if firm i exports to country c at time t and 0 otherwise; Dis tc′ , c is the
distance between countries c′ and c; Nc′ ≠Franceis the number of countries excluding
4Further details about the data sources are provided in Appendix A.

3606 THE AMERICAN ECONOMIC REVIEW NOVEMBER 2014
France in my sample; and
Δ Export sc′ , c, t_
Export sc′ , c, t is the growth of aggregate exports from coun-
try c′ to country c between years t and t + 1. The downward-sloping function g
erns how the proximity between countries c′ and c is related to the geographic dis-
tance between them. I consider the following two specifications for the function5
(2) g(Dis tc′, c) = {1/Dis tc′, c .
e−Dis tc′ , c/3.5
Coefficients Interpretation.—The coefficient α controls for impact of the numb
of countries a firm exports to on the likelihood it enters new markets subseque
α > 0 would mean that the more markets a firm exports to today, the more like
it is to enter new markets in the future. The coefficientβ1 controls for the direct
impact of proximity on trade: for both specifications of the function g in equatio
(2), the term g( Dis tFrance, c) is larger for a country c that is geographically closer
to France. β1 > 0 would mean that proximity has a beneficial effect on entry, in
the sense that a firm is more likely to enter close-by markets than rem
The coefficientβ2 controls for the indirect impact of proximity on trade: the term
∑ c′ 1[exp or ti, c′ , t > 0] g(Dis tc′ , c)
__
∑ c′ 1[exp or ti,c′ , t > 0] measures the average proximity between the countries
toward which firm i already exports in year t and country c. β2 > 0 would mean that
if a firm exports to countries which are close to c, it is subsequently more likely
enter that country c. The coefficients γ1 andγ2 are analogous toβ1 andβ2 , except
that the proximity between two countries is not measured by their physical dis
but by how much trade between them increases.γ1 > 0 would mean that the faster a
country’s imports grow, the more likely it is that any firm enters that country.γ2 > 0
would mean that if a firm already exports to countries whose exports to c grow
subsequently more likely to enter that country. Finally, the coefficient δ contro
the export status of firm i in the previous year, and the possibility that a firm lo
foreign contacts. I expect α, β1 , β2 , γ1 , γ2 > 0 and 0 < δ ≤ 1.
I control for country size, since firms are mechanically more likely to export t
large country than to a small one. I also add controls for the sector in which a fi
operates, as firms in different sectors may be more or less likely to export to an
ticular country. Removing the sector fixed effects does not affect the results m
ally. Replacing the flexible g(Dist) function by country fixed effects does not affect
the results materially either. Finally, it is likely that if country c is more isolated
from the rest of the world, in the sense that it is more distant from all other cou
tries, competition in c will be milder, and all else equal, it will be easier to acce
In order not to bias the estimated direct impact of distance( β1) , the coefficient β3 ,
expected to be negative, controls for this remoteness measure.
Results.—Table 1 shows the marginal effects from the Probit estimation of dif
ferent specifications of equation (1). Standard errors are clustered at the firm l
5I take the number 3.5 in e−x/3.5 from the SMM (simulated method of moments) estimate of the theory presented
in the next section.

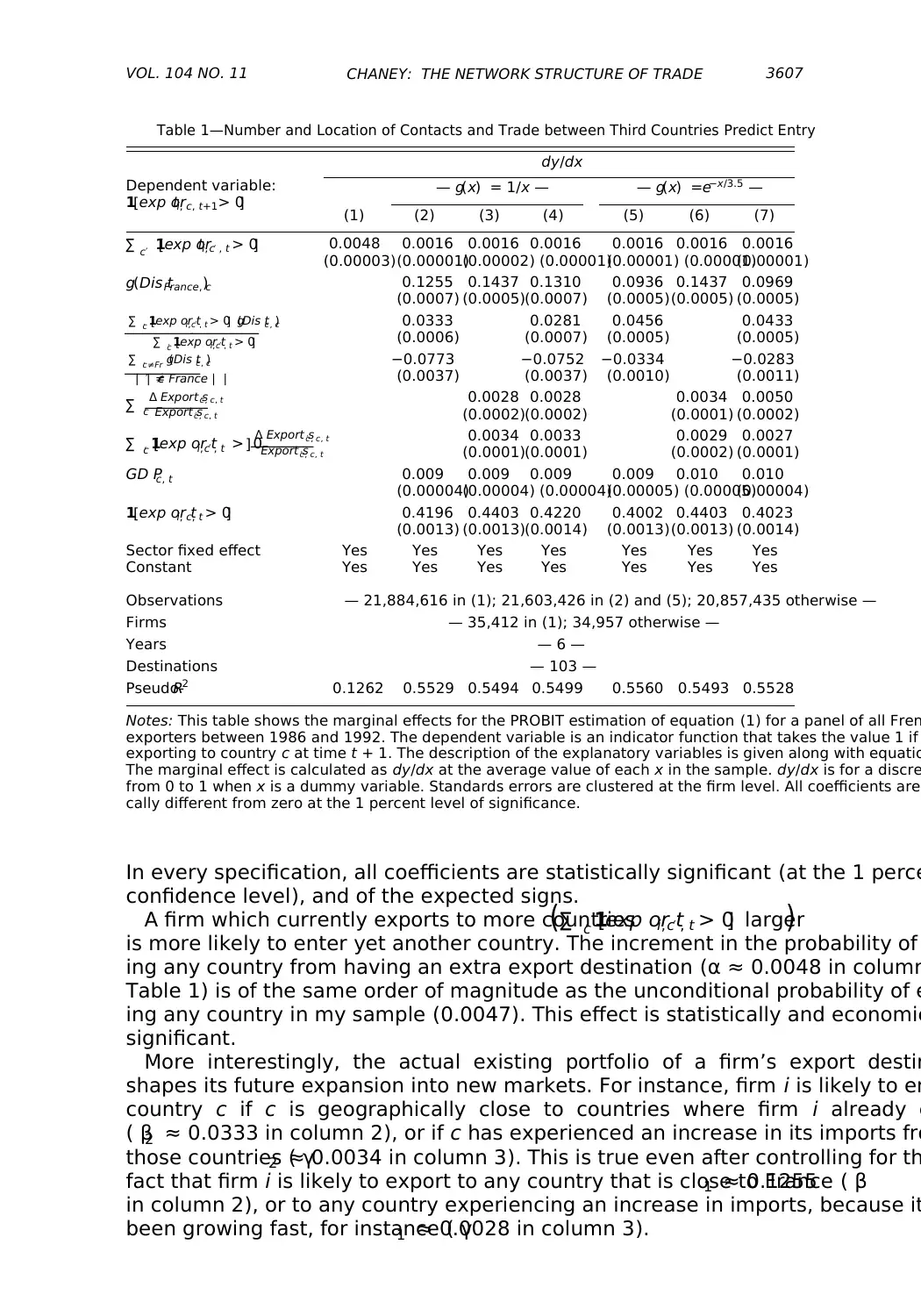
3607CHANEY: THE NETWORK STRUCTURE OF TRADEVOL. 104 NO. 11
In every specification, all coefficients are statistically significant (at the 1 perce
confidence level), and of the expected signs.
A firm which currently exports to more countries( ∑ c′ 1[exp or ti,c′ , t > 0] larger)
is more likely to enter yet another country. The increment in the probability of
ing any country from having an extra export destination (α ≈ 0.0048 in column
Table 1) is of the same order of magnitude as the unconditional probability of e
ing any country in my sample (0.0047). This effect is statistically and economic
significant.
More interestingly, the actual existing portfolio of a firm’s export destin
shapes its future expansion into new markets. For instance, firm i is likely to en
country c if c is geographically close to countries where firm i already e
( β2 ≈ 0.0333 in column 2), or if c has experienced an increase in its imports fro
those countries ( γ2 ≈ 0.0034 in column 3). This is true even after controlling for th
fact that firm i is likely to export to any country that is close to France ( β1 ≈ 0.1255
in column 2), or to any country experiencing an increase in imports, because it
been growing fast, for instance ( γ1 ≈ 0.0028 in column 3).
Table 1—Number and Location of Contacts and Trade between Third Countries Predict Entry
Dependent variable:
1[exp orti, c, t+1> 0]
dy/dx
— g( x) = 1/x — — g( x) =e−x/3.5 —
(1) (2) (3) (4) (5) (6) (7)
∑ c′ 1[exp orti, c′ , t > 0] 0.0048 0.0016 0.0016 0.0016 0.0016 0.0016 0.0016
(0.00003)(0.00001)(0.00002) (0.00001)(0.00001) (0.00001)(0.00001)
g( Dis tFrance, c) 0.1255 0.1437 0.1310 0.0936 0.1437 0.0969
(0.0007) (0.0005)(0.0007) (0.0005)(0.0005) (0.0005)
∑ c′ 1[exp or ti,c′ , t > 0] g( Dis tc′ , c)
__
∑ c′ 1[exp or ti,c′ , t > 0]
0.0333 0.0281 0.0456 0.0433
(0.0006) (0.0007) (0.0005) (0.0005)
∑ c′ ≠Fr g( Dis tc′ , c)
__
| | c′ ≠ France | |
−0.0773 −0.0752 −0.0334 −0.0283
(0.0037) (0.0037) (0.0010) (0.0011)
∑ c′
Δ Export sc′ , c, t_
Export sc′ , c, t
0.0028 0.0028 0.0034 0.0050
(0.0002)(0.0002) (0.0001) (0.0002)
∑ c′ 1[exp or ti,c′ , t > 0] Δ Export sc′ , c, t_
Export sc′ , c, t
0.0034 0.0033 0.0029 0.0027
(0.0001)(0.0001) (0.0002) (0.0001)
GD Pc, t 0.009 0.009 0.009 0.009 0.010 0.010
(0.00004)(0.00004) (0.00004)(0.00005) (0.00005)(0.00004)
1[exp or ti, c, t > 0] 0.4196 0.4403 0.4220 0.4002 0.4403 0.4023
(0.0013) (0.0013)(0.0014) (0.0013)(0.0013) (0.0014)
Sector fixed effect Yes Yes Yes Yes Yes Yes Yes
Constant Yes Yes Yes Yes Yes Yes Yes
Observations — 21,884,616 in (1); 21,603,426 in (2) and (5); 20,857,435 otherwise —
Firms — 35,412 in (1); 34,957 otherwise —
Years — 6 —
Destinations — 103 —
Pseudo-R2 0.1262 0.5529 0.5494 0.5499 0.5560 0.5493 0.5528
Notes: This table shows the marginal effects for the PROBIT estimation of equation (1) for a panel of all Fren
exporters between 1986 and 1992. The dependent variable is an indicator function that takes the value 1 if
exporting to country c at time t + 1. The description of the explanatory variables is given along with equatio
The marginal effect is calculated as dy/dx at the average value of each x in the sample. dy/dx is for a discre
from 0 to 1 when x is a dummy variable. Standards errors are clustered at the firm level. All coefficients are
cally different from zero at the 1 percent level of significance.

3608 THE AMERICAN ECONOMIC REVIEW NOVEMBER 2014
Of special interest is the size of the coefficient δ. δ measures the per
of a firm’s exports to a particular country. Across the various specificatio
equation (1), δ is around 40 percent. This implies that every year, a firm
60 percent chance of exiting a country where it is currently exporting. This larg
number implies a high degree of churning in exports, an observation that reson
with the findings in Eaton et al. (2010). The estimated δ is of course the margin
effect across a heterogeneous set of exporters, so it may hide a large amount o
heterogeneity.
To conclude, I find reduced-form evidence that individual firms follow a histor
dependent process which governs their gradual entry into foreign markets. I iso
two stylized facts. First, the more countries a firm exports to today, the more li
it is to enter yet other countries in the future. Second, where a firm exports tod
affects where that firm will export in the future: all else equal, if a firm exports
countries that are close to country c, it is more likely to enter that country c in
future. Motivated by those stylized facts, I now build a theoretical model of firm
level export dynamics.
II. A Dynamic Model of Exports
In this section, I develop a model of the sequential entry of firms into foreign
kets that incorporates the stylized facts uncovered earlier in the paper. I show
a model which features a history-dependent process for exporting generates st
predictions not only for the time series of exports, but also for the cross-section
exports.
A. Setup
Space.—  is a discrete set of locations. I will consider several alternatives fo
set . I start with a presentation of the theory without imposing any restriction
. I then fully solve the model for the special case  = ℤ. I use this special case
to illustrate the key forces of the model. I finally turn back to a more general se
where  ≠ ℤ. Using numerical simulations, I show that the results derived in th
special case  = ℤ offer a good approximation of what happens in more genera
cases, and provide a useful guidance for the structural estimation of the model
Firms.—In each location x ∈ , there is a finite set of firms. Those firms sell th
output to consumers in various locations. Time is discrete, and the number of fi
in each location grows at a constant rate γ.
Search Frictions.—In the absence of any frictions, all firms would sell to all co
sumers in every location. I assume instead that firms face the following matchi
frictions.6 Every period, a firm acquires new consumers in two distinct ways. Firs
the firm searches for new consumers locally, meaning that the search originate
where the firm itself is located. This first direct search corresponds to β1 , γ1 > 0 in
6I develop in the online Appendix a simple extension of the Krugman (1980) model which endogenizes tho
assumptions.

3609CHANEY: THE NETWORK STRUCTURE OF TRADEVOL. 104 NO. 11
the reduced-form evidence presented in Table 1. Second, the firm uses its exis
network of consumers to search remotely, meaning that the search originates
where the existing consumers are located. This second remote search correspo
to β2 , γ2 > 0 in the reduced form evidence presented in Table 1. It captures the
of local externalities as in the case of the geographic expansion of Wal-mart in
(2008) and Holmes (2011), or in the case of Chilean exporters in Morales, Sheu
and Zahler (2013). It may either correspond to the technological constraint on
expansion of a distribution network as in Holmes (2011); to the cost of customi
a product for local tastes and requirements as in Morales, Sheu, and Zahler (20
or more generally to the notion that exporting entails some amount of traveling
communicating with business partners, so that a firm which exports to a locatio
will acquire some knowledge about y and its surrounding locations.
Note that this is a model of the extensive margin of trade only. To fix ideas, t
of the firm as an intermediate input producer, and its consumers as other down
stream firms, potentially in other locations. I model explicitly how this firm ove
time sells to more consumers in more locations, but I do not model how much i
to each of them. Superimposing a model for the intensive margin of sales is lef
future research.
Before describing the dynamic acquisition of consumers formally, it is useful
introduce a few notations. Consider firm i of age t in a location which I arbitrari
call the origin. It has a network of consumers in various locations. The total num
of consumers of firm i ismi, t , distributed in various locations. I callfi, t( x) the num-
ber of consumers firm i has in location x,
fi, t :  → ℕ with∑
x∈
fi, t(x) ≡mi, t ,
so that∑ x∈ fi, t(x) is the number of consumers firm i of age t has in the subset ⊂ . The functionfi, t specifies both the number and the location of all the con-
sumers of the firm.fi, t is not a probability distribution, as it sums up tomi, t and not 1.
The distribution of consumersfi, t evolves as follows.
First, firm i searches locally for consumers from where it is located (the locat
arbitrarily called the origin). Each period, it finds∼
γμ new consumers where∼
γμ is a
positive integer-valued random variable of mean γμ. γ is the (constant) growth
of the population of firms, and μ > 0 is a parameter.7 The location x ∈  of each
of these consumers is drawn randomly according to a function g, where(0, x)
denotes the probability that a search originating from the origin (arbitrarily cal
identifies a customer in location x. I expect that the function g(0, x) depends on the
distance between the origin( 0) of the search and the destination(x) , and the size
of the destination x, but I will only impose such conditions later in Sections IIC a
IID and when I bring the model to the data in Section III.
Second, given that firm i already has consumers in various locations, it searc
for new consumers remotely from these locations. For each existing consumer
location y ∈ , the firm meets∼
γμπ new consumers where∼
γμπ is a positive integer
7Expressing the number of randomly drawn new consumers as a multiple of the population growth rate is
a normalization, which will simplify the exposition of the main results.

3610 THE AMERICAN ECONOMIC REVIEW NOVEMBER 2014
valued random variable of mean γμπ. π ≥ 0 is a parameter. The geographic loc
tion of these consumers is independently and randomly drawn according to the
function g, where g( y, x) is the probability that a search originating from y identifie
a customer in x. Remote search works exactly as local search, except that( i ) it is
shifted from the origin to location y, and( ii ) the efficiency of this remote search
is scaled by a constant factor π, which measures the relative importance of rem
versus local search.
Without loss of generality, neither does a firm lose consumers, nor do firms d
Adding a random death process to either contacts or firms does not change an
the results below, beyond some simple rescaling of the parameters.8
Firm Level Dynamics.—The dynamic evolution of the network of consum
described above can be summarized in the following difference equation forfi, t :
(3) fi, t+1( x) −fi, t(x) =∑
k0 =1
∼
γμi
1[˜xi,k0 = x] +∑
y∈
fi, t(y) ∑
ky =1
∼
γμπi, y
1[˜xi,ky = x] ,
with the initial conditionfi, 0( x) = 0, ∀x ∈ . 1 [ · ]is the indicator function.∼
γμi and
the∼
γμπi, y are independent draws from the random variables∼
γμ and∼
γμπ, respec-
tively. The˜xs are independent realizations from the probability distribution g, wh
determine the geographic location of each new contact. I give these draws som
arbitrary index: for instance, Pr( 1[˜xi,ky = x]) = g(y, x) is the probability that a
remote search from y identifies a consumer in x. The change in the number of
sumers in location x from time t to time t + 1 can be decomposed in two terms
first term corresponds to the local search for new contacts. Anyk0 of the∼
γμi new
contacts is located in x only if˜xi,k0 = x. The second term corresponds to the remote
search for new contacts. For each existing contact firm i has in location y (ther
fi, t( y) of them), any ky of the∼
γμπi, y new contacts acquired from y is located in x only
if ˜xi,ky = x. Since the remote search can be intermediated via any location y ∈
the new consumers found in x via y have to be summed over all possible remo
location y ∈ .
The same parameters( γμ, γμπ) in equation (3) govern the dynamic evolution of
the network of contacts of any firm. This does not mean of course that any two
will follow the same path ex post, as the luck of the draw will shape each indivi
firm’s network differently. In particular, the second term in equation (3) implies
strong history dependence in firms export dynamics.
Aggregate Dynamics.—Averaging across a large number of firms within a coh
however, the randomness of each draw disappears, and I can derive a simple e
sion for the recursive evolution of population averages. Consider all the firms o
t located in the origin, and call N the number of such firms. I define ft
N( x) as the
average number of contacts in location x ∈  within this cohort, and ft( x) the limit
of this population average when N gets large,
8See Atalay et al. (2011) for a related model, without geography, that features firm deaths.

3611CHANEY: THE NETWORK STRUCTURE OF TRADEVOL. 104 NO. 11
ft
N( x) ≡ ∑ i=1
N fi, t( x)
_
N ∈ ℚ and ft(x) ≡lim
N→∞
f t
N(x) ∈ ℝ+ .
I show in Appendix B how to use the law of large numbers and the fact that all
random shocks are i.i.d. in order to derive the following difference equation for
dynamics offt , the network of consumers of an entire cohort when the population
is large:
(4) ft+1(x) −ft( x) = γμg( 0, x) + γμπ∑
y∈
ft( y) g( y, x) ,
with the initial condition f0( x) = 0, ∀x ∈ . Note that as the population is large,
all uncertainty has been removed in the aggregate. This does not mean that al
within a cohort are identical, but that those differences are summarized by a st
function. This stable behavior for the population average obtains despite the in
ent randomness of the small sample of consumers of any individual firm, but a
despite the fact that as time goes on, the network of consumers of individual fi
within the same cohort diverges.
The recursive definition of ft in equation (4) is complex. In Section IIB, I present
an analytical solution for the distribution of the total number of consumers( mt)
within the population. This solution holds for any set  and function g. Solving f
other moments of ft requires me to take a stand on  and on the function g. In Sect
IIC, I present an analytical solution for other moments offt in the special case where
 = ℤ and g( y, x) only depends on the distance|x − y| . In Section IID, I conjec-
ture using numerical simulations that as long as g( y, x) only depends on the distance
||x − y|| and on the size of the destination location x, the solution for the specia
case  = ℤ is a good approximation of the general case where  ≠ ℤ.
B. The Number of Consumers
Geography plays no role in the number of a firm’s consumers. The geographi
biased distribution g affects the location of consumers, but not the total
of them. Summing equation (4) over , I get a difference equation for the avera
number of consumers of firms within a cohort,
(5) mt+1 −mt = γμ + γμπmt .
This process does not depend on any of the properties of the distribution g or o
set .
This recursive equation for the number of consumers resembles the mo
acquisition of a network of “friends” in Jackson and Rogers (2007), which itself
an extension of the Steindl (1965) model of the firm size distribution.9 In particular,
the same mean-field approximation as in Jackson and Rogers can be used to so
9The model is different from Jackson and Roger’s in that firms do not explicitly learn about new contacts f
the contacts of their existing contacts. For more elaborate models of the dynamic evolution of size, see for in
Gabaix (1999); Luttmer (2007); or Rossi-Hansberg and Wright (2007).