Normal Distribution Process Assignment

NORMAL DISTRIBUTION
STUDENT NAME:
SCHOOL:
AFFILIATION:
1

NORMAL DISTRIBUTION
A STUDY GUIDE FOR NORMAL DISTRIBUTION
Overview
The normal distribution is a perfectly symmetric, bell-shaped distribution. The pattern is defined
as normal as it appears in data for many real-life phenomena.
Important Terms
Normal distribution
Standard Normal Distribution
Random Variable
Continuous random variable
Mean
Standard Deviation
Empirical Rule
Normal Density Curve
Z-scores
Definition of a Normal Distribution
A normal distribution has the following characteristics:
 Perfect symmetric distribution.
 Bell curve.
 Describes a continuous random variable.
 Infinite distributions on both sides of the curve tending towards 0 but never reach 0.
 Has its center as mean.
 Mean, median and mode are equal.
2

NORMAL DISTRIBUTION
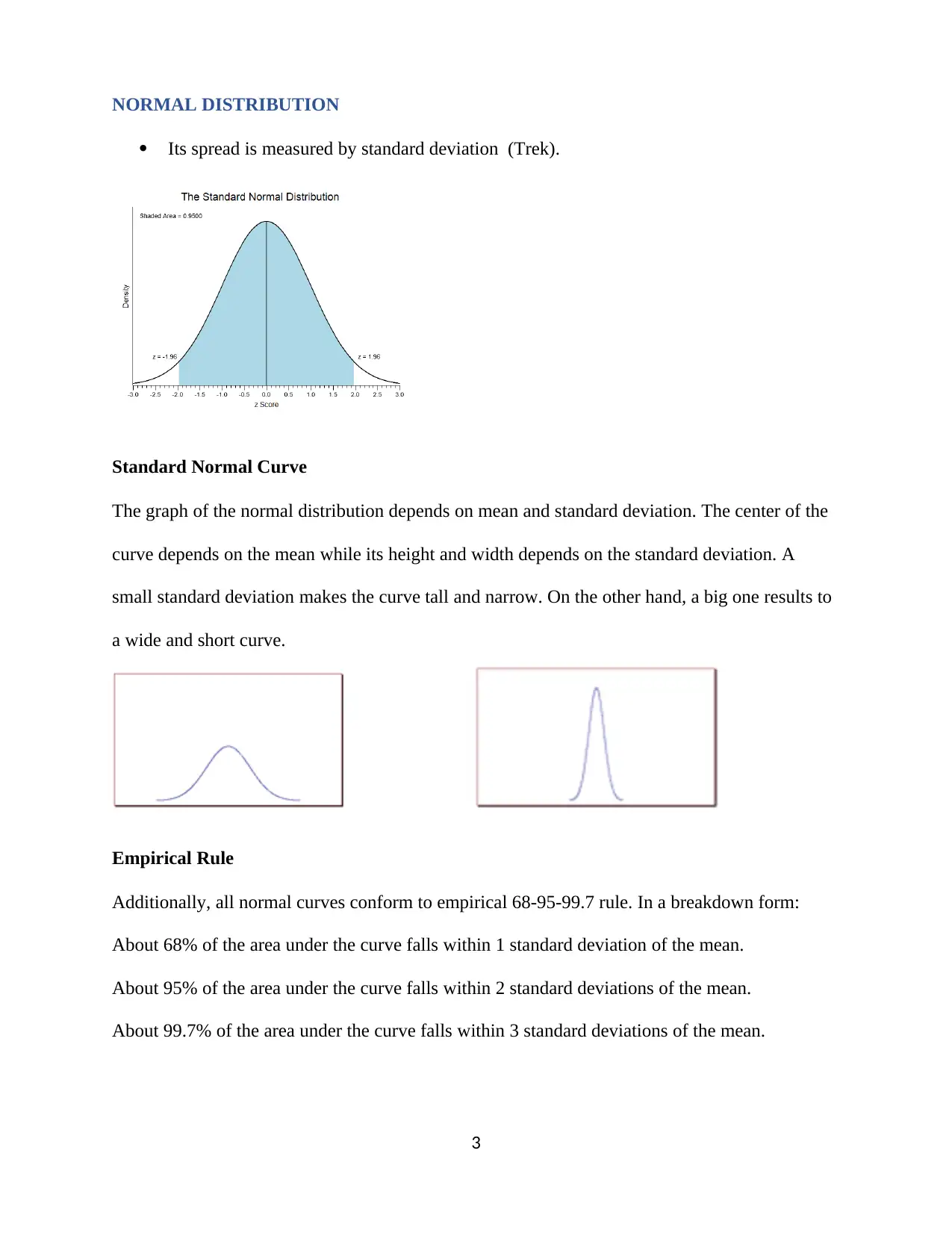
 Its spread is measured by standard deviation (Trek).
Standard Normal Curve
The graph of the normal distribution depends on mean and standard deviation. The center of the
curve depends on the mean while its height and width depends on the standard deviation. A
small standard deviation makes the curve tall and narrow. On the other hand, a big one results to
a wide and short curve.
Empirical Rule
Additionally, all normal curves conform to empirical 68-95-99.7 rule. In a breakdown form:
About 68% of the area under the curve falls within 1 standard deviation of the mean.
About 95% of the area under the curve falls within 2 standard deviations of the mean.
About 99.7% of the area under the curve falls within 3 standard deviations of the mean.
3

NORMAL DISTRIBUTION
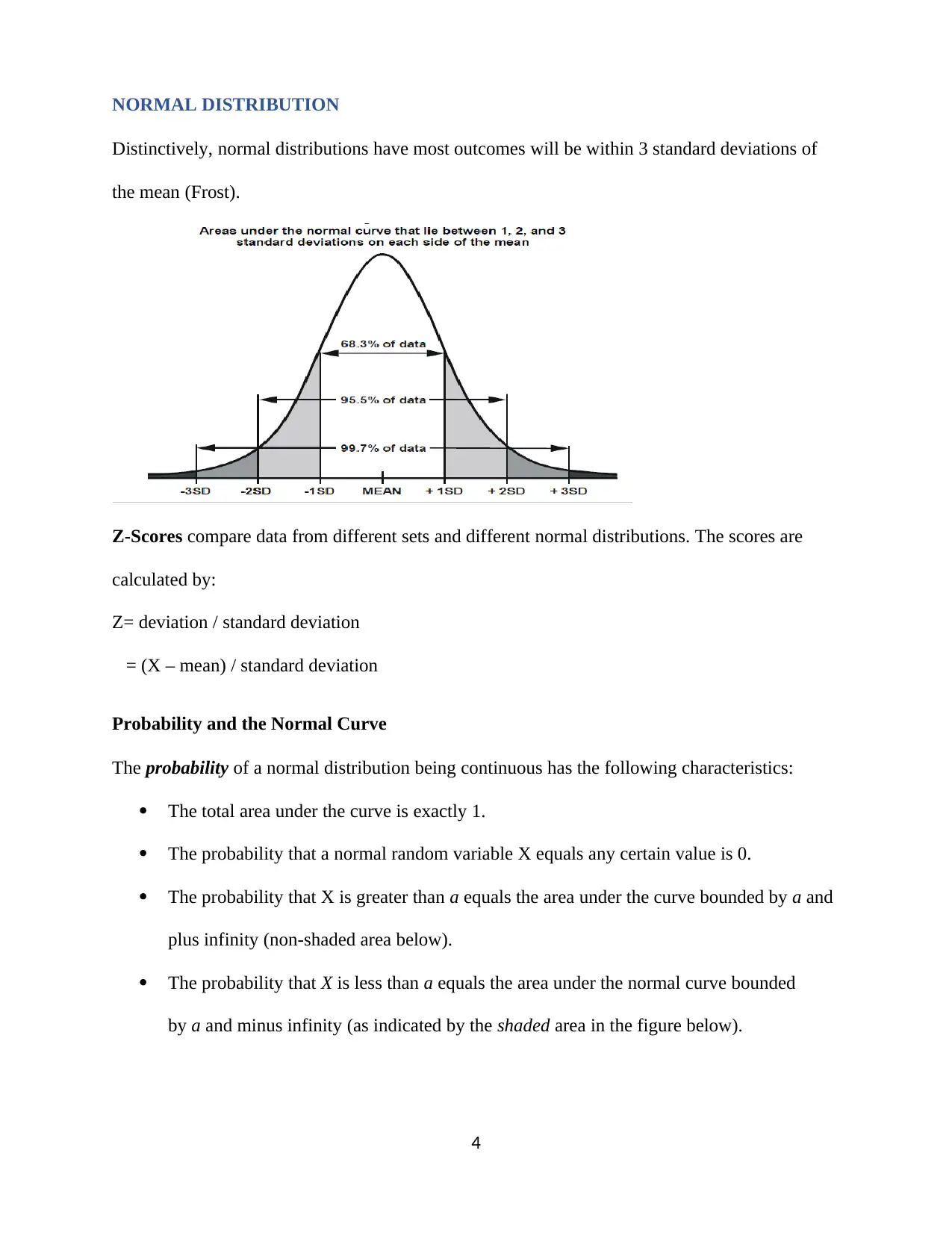
Distinctively, normal distributions have most outcomes will be within 3 standard deviations of
the mean (Frost).
Z-Scores compare data from different sets and different normal distributions. The scores are
calculated by:
Z= deviation / standard deviation
= (X – mean) / standard deviation
Probability and the Normal Curve
The probability of a normal distribution being continuous has the following characteristics:
 The total area under the curve is exactly 1.
 The probability that a normal random variable X equals any certain value is 0.
 The probability that X is greater than a equals the area under the curve bounded by a and
plus infinity (non-shaded area below).
 The probability that X is less than a equals the area under the normal curve bounded
by a and minus infinity (as indicated by the shaded area in the figure below).
4

NORMAL DISTRIBUTION
The standardized normal curve has mean, 0 and standard deviation, 1. When the curve is
standardized, a Z-table is used to find the percentages or areas under the curve.
Finding the area under the curve of a Normal Distribution
The probability that a value will fall under a certain interval is indicated by the proportion of the
area that falls under the curve between two points, a and b, on a probability distribution plot.
a). Z-score on left side of the mean
Any value to the left of the mean is lesser than the mean. First, convert the value into a z-score
using the Z formula above. The given z-score with decimals is split into two decimals places.
The decimals are looked up in the z-table. The intersection between the top row and left column
gives the area under the curve.
b). Z-score on the right side of the mean
The right side of the mean means the value was greater than the mean. The value is converted
into a Z-score using the Z formula above. Then, the area under the curve is obtained by looking
up on the Z-table the intersection between the left column and top row. Also, if given the area of
the left side of the mean, subtract 1 from it. The result is the area of the curve on the right side of
the mean.
c). Z-score values on opposite sides of the mean
5

NORMAL DISTRIBUTION
Any two values on opposite sides of the mean are less and greater than the mean. The two values
are converted into z-scores using the Z formula. First, the z-scores are obtained by looking in the
Z-table the intersections of both scores individually. Then, the values found previously are added
together. If negative, the sign is ignored and absolute values considered. For instance, finding the
area between two z values of -6 and -7, 6 and 7 are looked up instead.
d). Z score values on one side of the mean
Both two values on one side of the mean are either greater or less than the mean. After splitting
the two values at the tenths place, look in the Z-table for the z-scores by finding intersections.
Then, subtract the smaller z-value obtained from the larger value.
To find the probability associated with a random normal variable, various studies propose use of
graphing calculator, an online normal distribution, a normal distribution table or the
NORM.DIST function in MS Excel.
Testing understanding
Problem
Use your study guide to answer the following questions about statewide math SAT scores, which
have μ = 467 (out of 800) and σ = 129.3.
(a) If one student is randomly selected, find the probability of her math SAT score being
between 400 and 600.
(b) Only students above the 85th percentile are considered eligible for admission to SUNY
Cobleskill. What math SAT score corresponds to the 85th percentile?
Solution
6

NORMAL DISTRIBUTION
Here, the calculation is focused on determining the probability that the student’s score falls
between 400(a) and 600(b).
Z scores:
Z = deviation / standard deviation
= (X – mean) / standard deviation
For 400:
Z = (400 – 467) / 129.3
= - 67 / 129.3
= - 0.5182 or – 0.52
For 600:
Z = (600 – 467) / 129.3
= 133 / 129.3
= 1.0286 or 1.03
Probability:
P (400 < X < 600) = P (-0.52 < Z < 1.03)
P (0.52 < Z < 1.03) = P (Z< 1.03) – P (Z< - 0.52)
= 0.8485 - 0.3015
= 0.5470
There is a 0.55 probability that the student scored between 400 and 600 out of 800 points in the
MATH SAT test.
Computing the eligible score using 85th percentile:
X = mean + Z*standard deviation
Mean = 467
7

NORMAL DISTRIBUTION
Standard deviation = 129.3
X is the math score corresponding to the 85th percentile.
Z is the probability score corresponding o the 85th percentile.
Look up 0.85 in the Z-table. The values 0.8485 and 0.8508 corresponding to Z values 1.03 and
1.04 are a close match to 0.85. From a Z-score percentile table for normal distributions, the 85th
percentile is 1.036.
To get X the eligible math score:
X = 467 + 1.036*129.3
= 467 + 133.9548
= 600.9548
The math SAT score corresponding to the 85th percentile is 600.9548.
References
Frost, J. (n.d.). Normal Distribution. Retrieved from Making Statistics Inituitive.
Trek, S. (n.d.). The Normal Distributions. Retrieved from Teach Yourself Statistics:
https://stattrek.com/probability-distributions/normal.aspx
8