MAII3007 Numeracy 2 Coursework Portfolio - Summer 2019, GSM London

This document is a complete Numeracy 2 (MAII3007) coursework portfolio, submitted for the Summer 2019 semester at GSM London. It addresses nine questions in Section 1, covering topics such as scientific notation, Net Present Value (NPV) calculations, solving linear equations and inequalities, analyzing graphs of linear equations, creating and interpreting linear equations, constructing and interpreting histograms, analyzing scatter plots and correlation, and calculating probabilities. Section 2 consists of an in-class activity, and Section 3 contains three additional tasks, although the solutions for Sections 2 and 3 are not included in this document. The portfolio demonstrates the application of mathematical tools to solve problems, understanding of algebra, and the ability to present statistical data. The solutions provided include detailed workings, calculations, and justifications for each answer, adhering to the module's requirements and the provided marking criteria.

Numeracy 2 (MAII3007) Coursework
Portfolio
Summer 2019
Student Name
Student ID
Tutor
This is your Numeracy 2 e-portfolio which you must submit by Tuesday 20th
August 2019 via the Student Portal.
1

Please read this carefully
This is your Numeracy 2 e-portfolio for the semester commencing August 2019 (Summer 2019).
Please save a copy on your computer and back it up regularly (e.g. by saving it on your
computer/ in the cloud (e.g. Google Drive) / emailing it to yourself). You should print a working
copy and bring it to all lectures and tutorials. However, at the end of the course, you will need
to submit a completed electronic copy.
Please read carefully the module handbook, the marking criteria and the grade descriptors.
Academic Misconduct
You are responsible for ensuring that you understand the policy and regulations about
academic misconduct. You must:
• Complete this work alone except where required or allowed by the assignment briefing
paper and ensure it has not been written or composed by or with the assistance of any
other person.
• Make sure all sentences or passages quoted from other people’ work in this assignment
(with or without trivial changes) are in quotation marks, and are specifically acknowledged
by reference to the author, work and page.
The portfolio’s structure
Section 1 - is worth 65% of the final mark and consists of 9 questions.
Section 2 - is an in-class task and is worth 15% of the final mark.
Section 3 - is worth 20% of the final mark and consists of three tasks
2

Section 1
9 questions 65 marks
You are required to complete this section immediately after completing the class sessions
related to each question. Answer all questions and show your calculation and/or explain your
results. Marks will be awarded for good presentation.
You must show your workings.
QUESTION 1
[4 marks]
Which of these two numbers is bigger?
a) 5 - 3
b) 8.1 x 10-2
To answer this question, you must compare both numbers. For this purpose, convert both
numbers into decimals.
[TYPE YOUR ANSWER TO QUESTION 1 HERE]
a)5-3 b)8.1 x 10-2
= 1
53 = 1
125 = 0.008 = 8.1 x 1
102 = 8.1
100 = 0.081
Therefore, it is evident that 8.1 x 10-2 is bigger.
3
Scientific notation

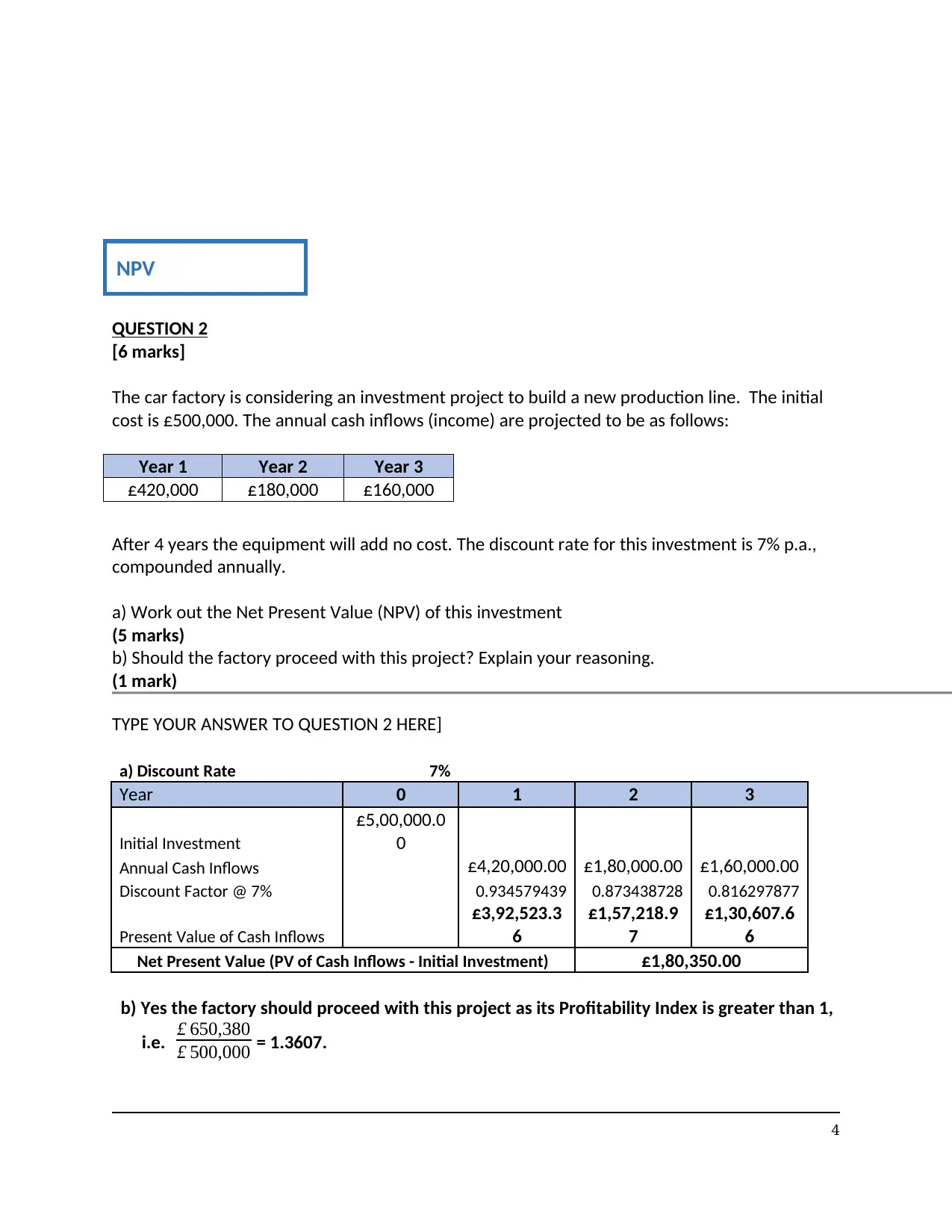
QUESTION 2
[6 marks]
The car factory is considering an investment project to build a new production line. The initial
cost is £500,000. The annual cash inflows (income) are projected to be as follows:
Year 1 Year 2 Year 3
£420,000 £180,000 £160,000
After 4 years the equipment will add no cost. The discount rate for this investment is 7% p.a.,
compounded annually.
a) Work out the Net Present Value (NPV) of this investment
(5 marks)
b) Should the factory proceed with this project? Explain your reasoning.
(1 mark)
TYPE YOUR ANSWER TO QUESTION 2 HERE]
a) Discount Rate 7%
Year 0 1 2 3
Initial Investment
£5,00,000.0
0
Annual Cash Inflows £4,20,000.00 £1,80,000.00 £1,60,000.00
Discount Factor @ 7% 0.934579439 0.873438728 0.816297877
Present Value of Cash Inflows
£3,92,523.3
6
£1,57,218.9
7
£1,30,607.6
6
Net Present Value (PV of Cash Inflows - Initial Investment) £1,80,350.00
b) Yes the factory should proceed with this project as its Profitability Index is greater than 1,
i.e. £ 650,380
£ 500,000 = 1.3607.
4
NPV

QUESTION 3
[10 marks]
a) Solve the following equation: 3 x +2
7 = 2 x
2
(3 marks)
b) Solve the following inequality: 7 ( 3 x−2 ) >−8+3 x (3
marks)
c) What are the integer values of x that satisfy the inequality –2 < x ≤ 5
(1 mark)
d) Calculate the intersect point for lines: y=−8 x−5∧ y =4 x + 4 (3
marks)
TYPE YOUR ANSWER TO QUESTION 3 HERE]
a) 3 x +2
7 = 2 x
2 b) 7(3x – 2) > -8 + 3x
→ 6x + 4 = 14x → 21x - 14 > -8 + 3x
→ 4 = 14x – 6x → 21x - 3x > -8 + 14
→ 4 = 8x → 18x > 6
→ x = ½ or 0.5 → x > 6
18
→ x > 1
3
5
Linear equations and inequalities

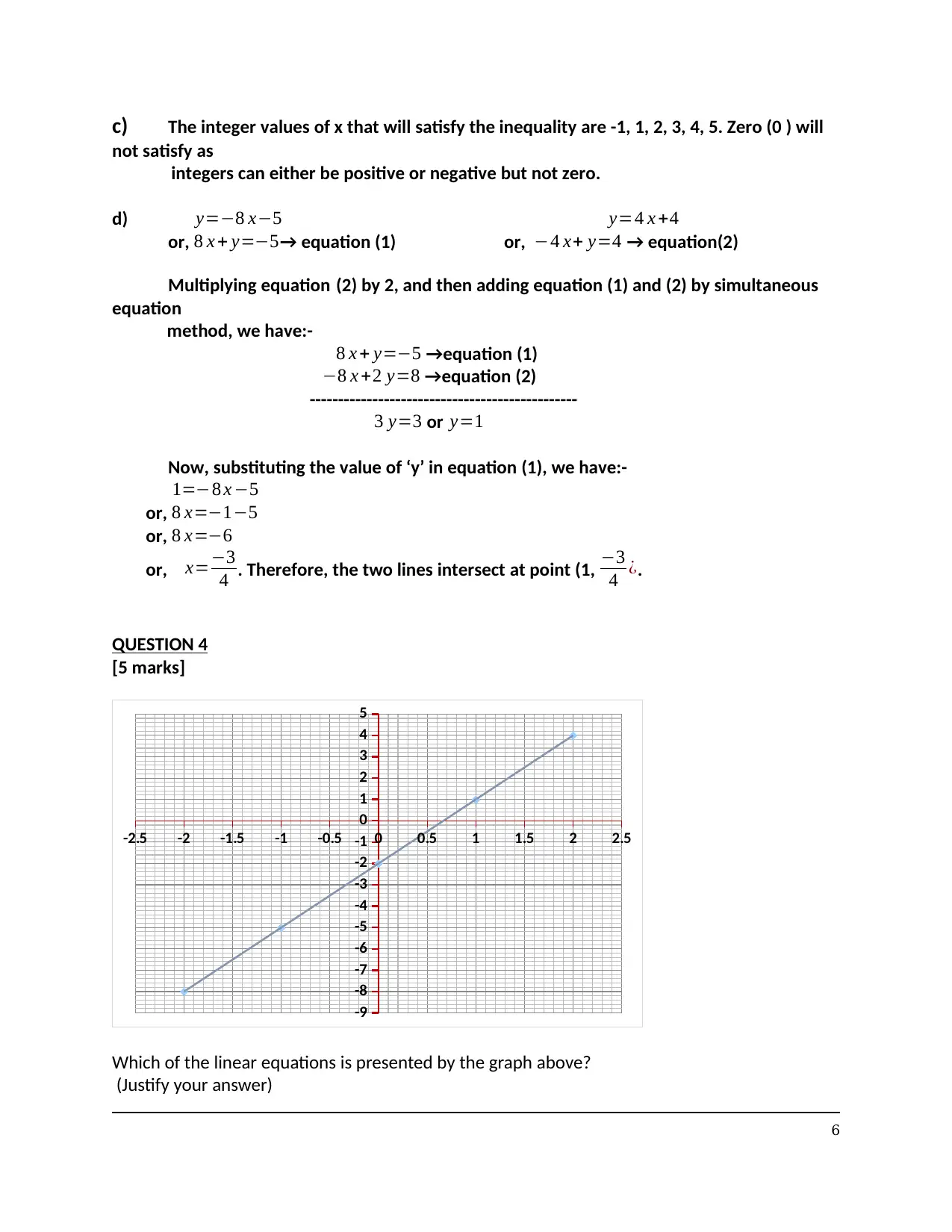
c) The integer values of x that will satisfy the inequality are -1, 1, 2, 3, 4, 5. Zero (0 ) will
not satisfy as
integers can either be positive or negative but not zero.
d) y=−8 x−5 y=4 x +4
or, 8 x + y=−5→ equation (1) or, −4 x+ y=4 → equation(2)
Multiplying equation (2) by 2, and then adding equation (1) and (2) by simultaneous
equation
method, we have:-
8 x + y=−5 →equation (1)
−8 x +2 y=8 →equation (2)
-----------------------------------------------
3 y=3 or y=1
Now, substituting the value of ‘y’ in equation (1), we have:-
1=−8 x −5
or, 8 x=−1−5
or, 8 x=−6
or, x=−3
4 . Therefore, the two lines intersect at point (1, −3
4 ¿.
QUESTION 4
[5 marks]
-2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
Which of the linear equations is presented by the graph above?
(Justify your answer)
6

a. y=−3 x −2
b. y=3 x +2
c. y=3 x−2
d. y=−3 x +2
TYPE YOUR ANSWER TO QUESTION 4 HERE]
As can be seen from the graph, the co-ordinates of X-axis and Y-axis are as follows:-
X Y
0 -2
1 1
2 4
-1 -5
-2 -8
Now let us put the values of X in each equation to find the value of Y.
a) y=−3 x −2 or, y=−3(0)−2 or, y=0−2 or, y=−2
or, y=−3(1)−2 or, y=−3−2 or, y=−5
or, y=−3 (2 )−2 or, y=−6−2 or, y=−8
or, y=−3 (−1 )−2 or, y=3−2 or, y=1
or, y=−3(−2)−2 or, y=6−2 or, y=4
b) y=3 x +2 or, y=3 ( 0 )+ 2 or, y=0+2 or, y=2
or, y=3 ( 1 ) +2 or, y=3+ 2 or, y=5
or, y=3 ( 2 ) +2 or, y=6+2 or, y=8
or, y=3 (−1 )+2 or, y=−3+2 or, y=−1
or, y=3 ( −2 ) +2 or, y=−6+2 or, y=−4
c) y=3 x−2 or, y=3 (0)−2 or, y=0−2 or, y=−2
or, y=3 (1)−2 or, y=3−2 or, y=1
or, y=3 ( 2 ) −2 or, y=6−2 or, y=4
or, y=3 (−1 )−2 or, y=−3−2 or, y=−5
or, y=3 (−2)−2 or, y=−6−2 or, y=−8
d) y=−3 x +2 or, y=−3 ( 0 ) +2 or, y=0+2 or, y=2
or, y=−3 (1 )+2 or, y=−3+2 or, y=−1
or, y=−3 ( 2 ) +2 or, y=−6+2 or, y=−4
or, y=−3 (−1 )+ 2 or, y=3+ 2 or, y=5
or, y=−3 (−2 ) + 2 or, y=6+2 or, y=8
7

From the above calculations we find that equation (c) satisfies the above graph and hence we
can say that the graph is represented by the linear equation y=3 x−2.
QUESTION 5
[6 marks]
You have overrun your monthly phone limit of free minutes. Now, you have to pay 2 pence for
each minute you call. How long can you call if you have already gone beyond the bill by £4.50
and you do not want to exceed £10 of total additional cost?
a) Create the linear equation for this task. Explain what the slope and y-intercept represent.
(4 marks)
b) Calculate how many more minutes you can talk until you will exceed £10 of total additional
cost? (2 marks)
TYPE YOUR ANSWER TO QUESTION 5 HERE]
8

Here the ceiling for additional cost to pay for calls over and above the month free limit is £10.
Additionally, £4.5 has already been spent. Call rate per minute is 2 pence or £0.02. From the
information provided, the linear equation for the task is as follows:
£10 = £0.02x + £4.5
Here, the slope, i.e. £0.02 represents the rate at which the call is being charged per minute
and y-intercept, i.e. £4.5 represents the fixed amount (cost) that has already been spent. A
further increase in call duration (minutes) will lead to an increase in cost over and above the
fixed amount.
Number of more minutes that can be spent until the cost reaches £10:-
£10 = £0.02x + £4.5
or, £10 - £4.5 = £0.02x
or, £5.5 = £0.02x
or, x= £ 5.5
£ 0.02 =275 minutes .
QUESTION 6
[8 marks]
The data below represents the monthly average a person spends on clothes:
9
Histogram

72 50 68 68
80 69 78 70
95 64 85 71
106 79 80 69
a) Produce a tally of the data set. The tally must include 4 classes.
(3 marks)
b) Draw a histogram of the data set.
(4 marks)
c) Comment on the distribution of the data.
(1 mark)
TYPE YOUR ANSWER TO QUESTION 6 HERE]
Here the lowest monthly average is 50 and highest monthly average is 106. We now find the
width as the tally must include 4 classes as mentioned.
Calculation for tally width
106−50
4 and 106−50
4−1 = 56
4 and 56
3 = 14 and 18.67. Therefore, the width of the class must
be between 14 and 18.67. For our simplicity purpose, we take 16 as the class width.
a) Therefore the tally dataset is as follows:-
Class Tally Frequency
50 – 65 || 2
66 – 81 |||| |||| | 11
82 – 97 || 2
98 – 113 | 1
10

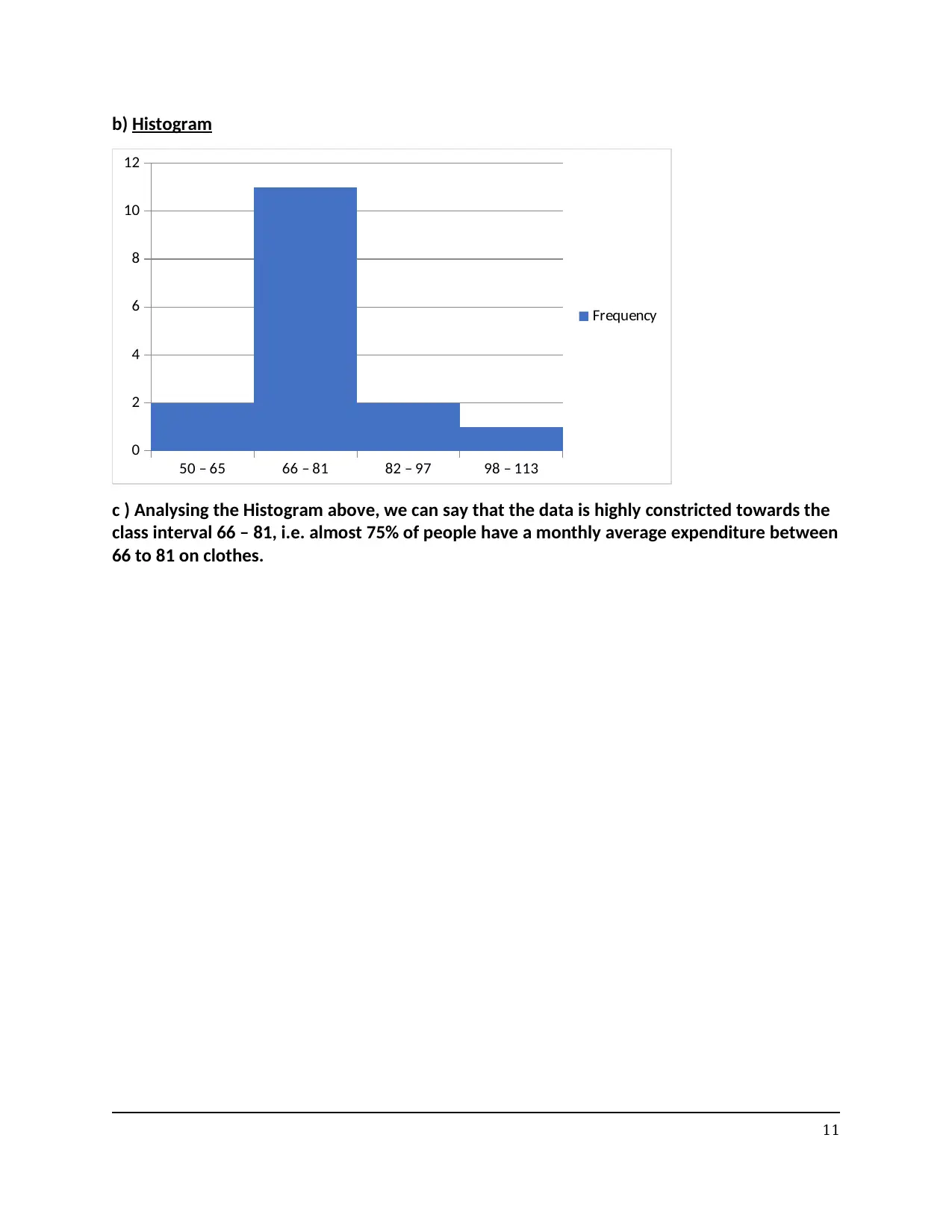
b) Histogram
50 – 65 66 – 81 82 – 97 98 – 113
0
2
4
6
8
10
12
Frequency
c ) Analysing the Histogram above, we can say that the data is highly constricted towards the
class interval 66 – 81, i.e. almost 75% of people have a monthly average expenditure between
66 to 81 on clothes.
11

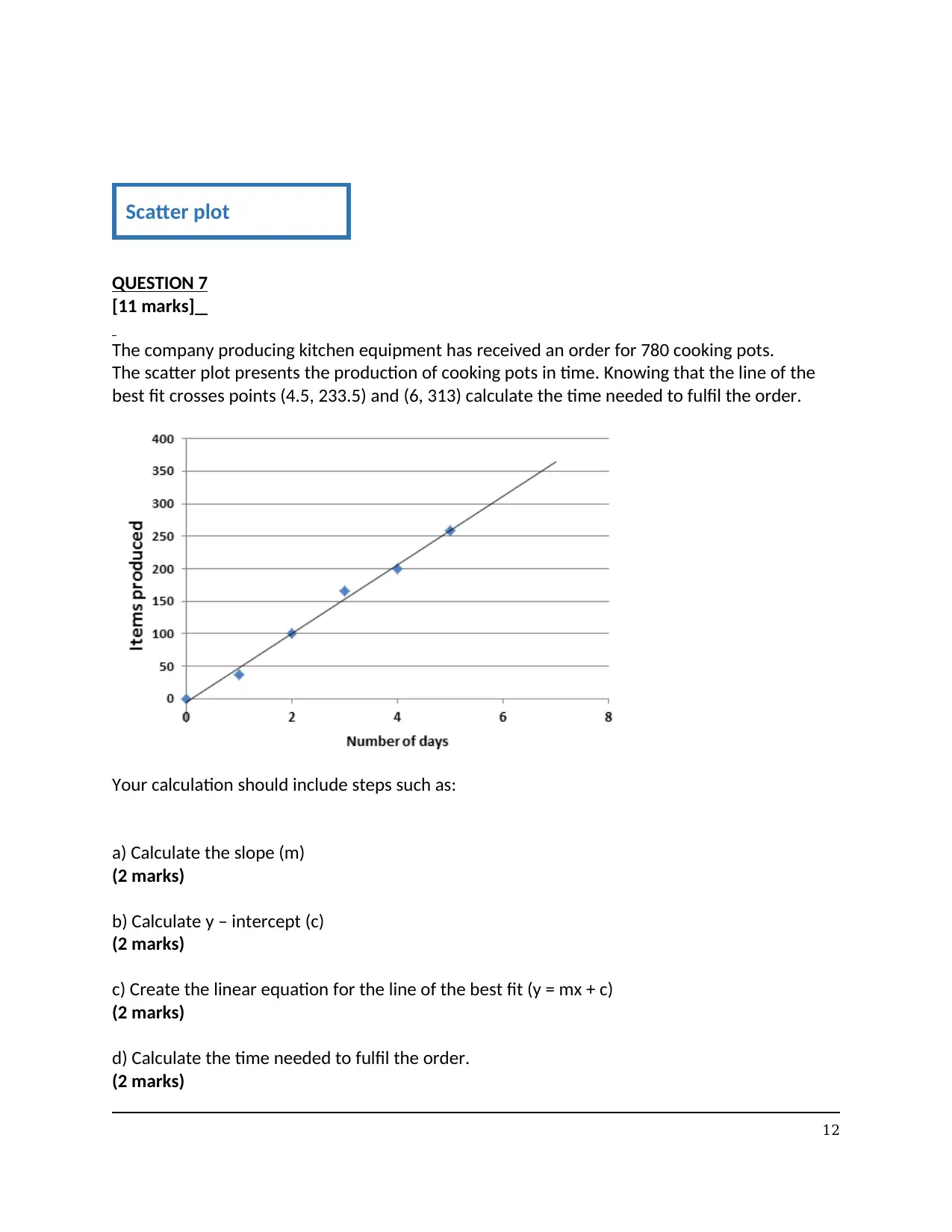
QUESTION 7
[11 marks]
The company producing kitchen equipment has received an order for 780 cooking pots.
The scatter plot presents the production of cooking pots in time. Knowing that the line of the
best fit crosses points (4.5, 233.5) and (6, 313) calculate the time needed to fulfil the order.
Your calculation should include steps such as:
a) Calculate the slope (m)
(2 marks)
b) Calculate y – intercept (c)
(2 marks)
c) Create the linear equation for the line of the best fit (y = mx + c)
(2 marks)
d) Calculate the time needed to fulfil the order.
(2 marks)
12
Scatter plot