Numeracy and Data Analysis
VerifiedAdded on 2022/11/24
|11
|1408
|462
AI Summary
This report focuses on the importance of numerical and data analysis in decision making. It includes arranging data in tabular and graphical form, computation of mean, mode, median, range, and standard deviation. Additionally, it presents a forecasting model for linear equations.
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

NUMERACY AND DATA
ANALYSIS
ANALYSIS
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

TABLE OF CONTENTS
INTRODUCTION.......................................................................................................................................3
MAIN BODY..............................................................................................................................................3
1. Arranging data regarding transportation expenditure in tabular form:.............................................3
2. Graphical representation of selected expenditure data.....................................................................3
3. Representing the required computation as follows..........................................................................4
4. Forecasting model for linear equation is presented as below:..........................................................8
CONCLUSION.........................................................................................................................................10
REFERENCES..........................................................................................................................................11
INTRODUCTION.......................................................................................................................................3
MAIN BODY..............................................................................................................................................3
1. Arranging data regarding transportation expenditure in tabular form:.............................................3
2. Graphical representation of selected expenditure data.....................................................................3
3. Representing the required computation as follows..........................................................................4
4. Forecasting model for linear equation is presented as below:..........................................................8
CONCLUSION.........................................................................................................................................10
REFERENCES..........................................................................................................................................11
INTRODUCTION
Data analysis is the procedure of inspecting, cleansing, transforming and modeling
statistical data with the objective of utilizing information for having appropriate decision
making. The present report is based on evaluating crucial data in organized manner to obtain
sufficient information for getting competitive benefits. The current study will include
presentation of data in both graphical & tabular form for transportation expenses. It will include
computation of mean, mode, median, range, standard deviation. Discussion regarding linear
forecasting model will be comprised in present report.
MAIN BODY
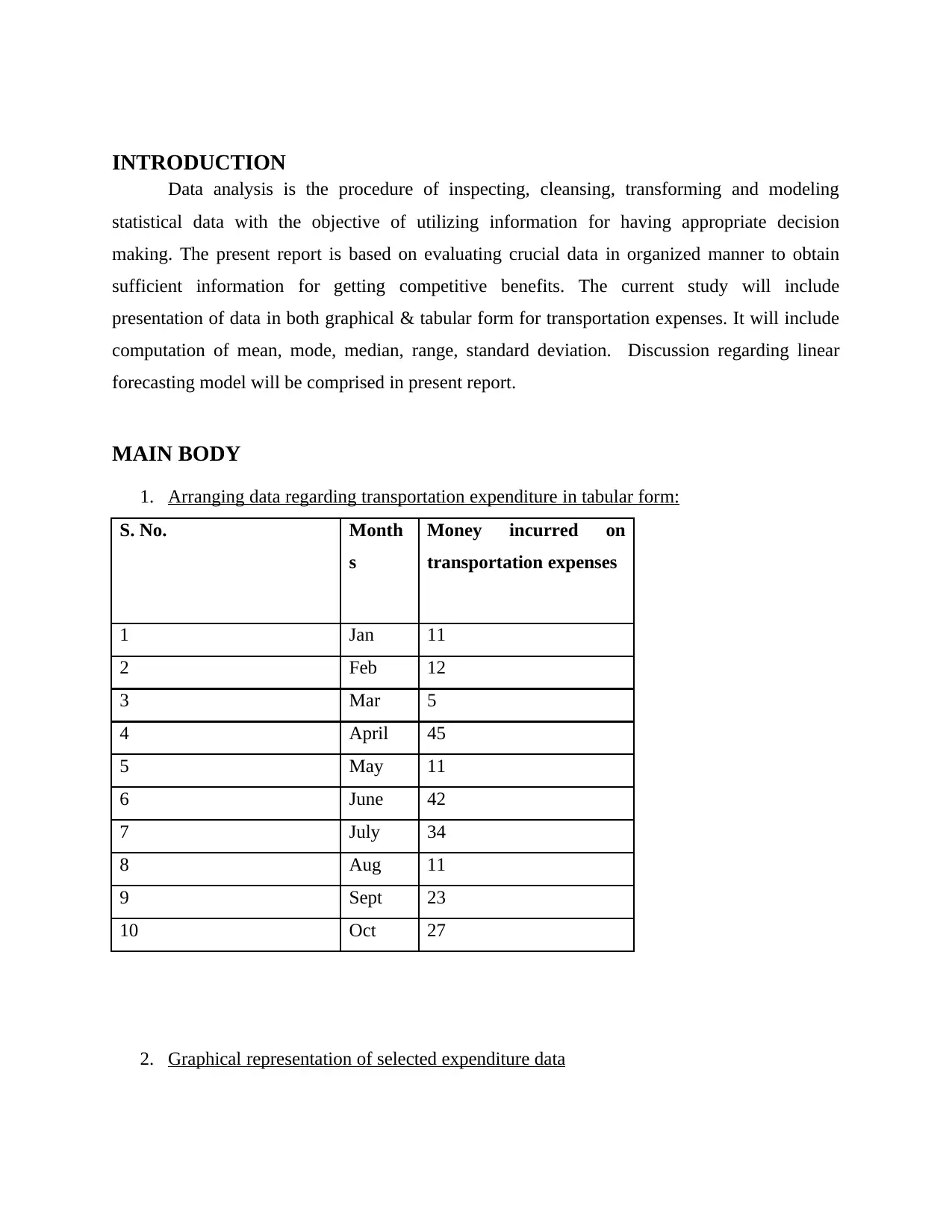
1. Arranging data regarding transportation expenditure in tabular form:
S. No. Month
s
Money incurred on
transportation expenses
1 Jan 11
2 Feb 12
3 Mar 5
4 April 45
5 May 11
6 June 42
7 July 34
8 Aug 11
9 Sept 23
10 Oct 27
2. Graphical representation of selected expenditure data
Data analysis is the procedure of inspecting, cleansing, transforming and modeling
statistical data with the objective of utilizing information for having appropriate decision
making. The present report is based on evaluating crucial data in organized manner to obtain
sufficient information for getting competitive benefits. The current study will include
presentation of data in both graphical & tabular form for transportation expenses. It will include
computation of mean, mode, median, range, standard deviation. Discussion regarding linear
forecasting model will be comprised in present report.
MAIN BODY
1. Arranging data regarding transportation expenditure in tabular form:
S. No. Month
s
Money incurred on
transportation expenses
1 Jan 11
2 Feb 12
3 Mar 5
4 April 45
5 May 11
6 June 42
7 July 34
8 Aug 11
9 Sept 23
10 Oct 27
2. Graphical representation of selected expenditure data

Jan
Feb
Mar
April
May
June
July
Aug
Sept
Oct
1 2 3 4 5 6 7 8 9 10
0
5
10
15
20
25
30
35
40
45
Money incurred on transportation
expenses
Money incurred on
transportation expenses
Jan
Feb
Mar
April
May
June
July
Aug
Sept
Oct
1 2 3 4 5 6 7 8 9 10
0
5
10
15
20
25
30
35
40
45
50
Money incurred on transportation
expenses
Money incurred on
transportation expenses
3. Representing the required computation as follows
I. Computation of mean:
S. No. Month
s
Money incurred on
transportation expenses
1 Jan 11
Feb
Mar
April
May
June
July
Aug
Sept
Oct
1 2 3 4 5 6 7 8 9 10
0
5
10
15
20
25
30
35
40
45
Money incurred on transportation
expenses
Money incurred on
transportation expenses
Jan
Feb
Mar
April
May
June
July
Aug
Sept
Oct
1 2 3 4 5 6 7 8 9 10
0
5
10
15
20
25
30
35
40
45
50
Money incurred on transportation
expenses
Money incurred on
transportation expenses
3. Representing the required computation as follows
I. Computation of mean:
S. No. Month
s
Money incurred on
transportation expenses
1 Jan 11
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
2 Feb 12
3 Mar 5
4 April 45
5 May 11
6 June 42
7 July 34
8 Aug 11
9 Sept 23
10 Oct 27
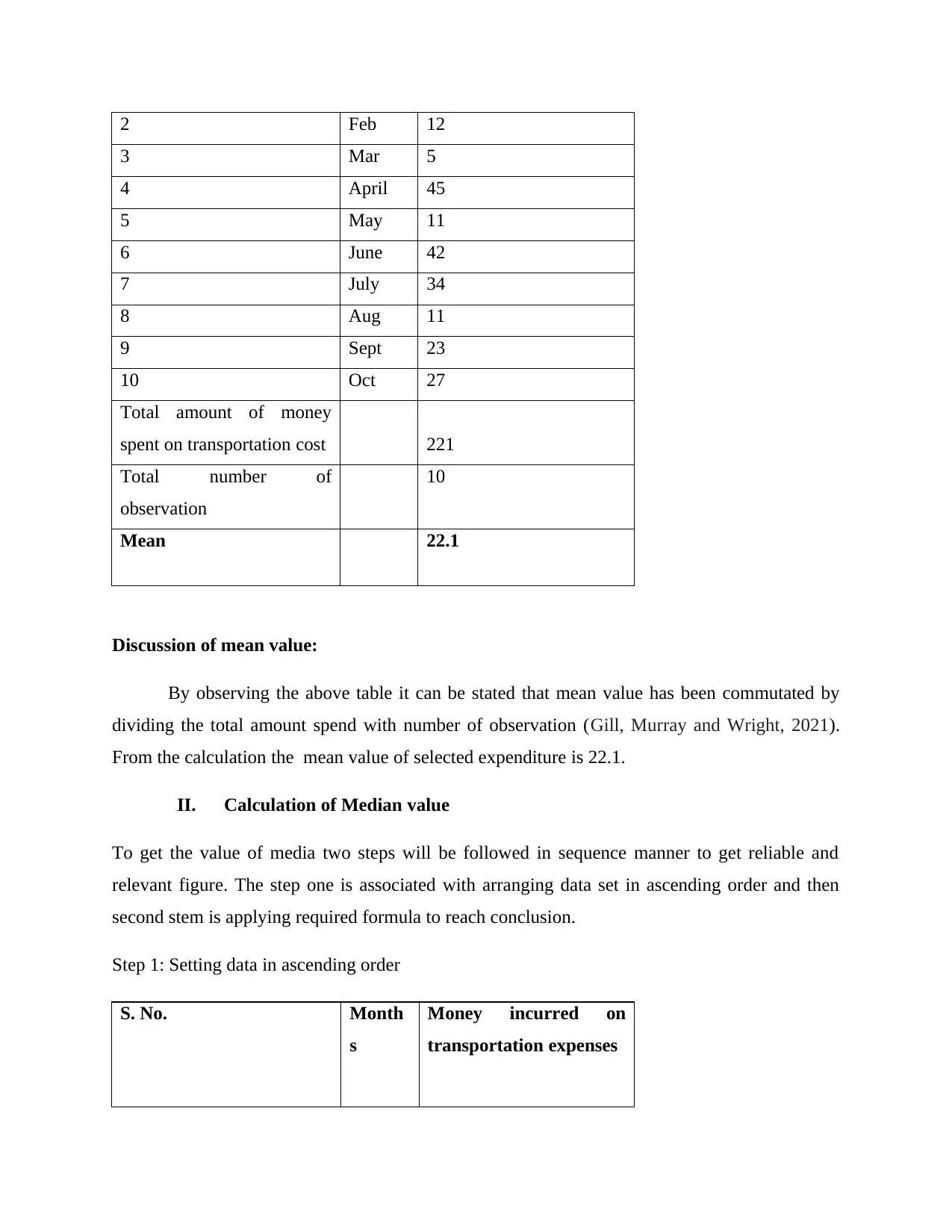
Total amount of money
spent on transportation cost 221
Total number of
observation
10
Mean 22.1
Discussion of mean value:
By observing the above table it can be stated that mean value has been commutated by
dividing the total amount spend with number of observation (Gill, Murray and Wright, 2021).
From the calculation the mean value of selected expenditure is 22.1.
II. Calculation of Median value
To get the value of media two steps will be followed in sequence manner to get reliable and
relevant figure. The step one is associated with arranging data set in ascending order and then
second stem is applying required formula to reach conclusion.
Step 1: Setting data in ascending order
S. No. Month
s
Money incurred on
transportation expenses
3 Mar 5
4 April 45
5 May 11
6 June 42
7 July 34
8 Aug 11
9 Sept 23
10 Oct 27
Total amount of money
spent on transportation cost 221
Total number of
observation
10
Mean 22.1
Discussion of mean value:
By observing the above table it can be stated that mean value has been commutated by
dividing the total amount spend with number of observation (Gill, Murray and Wright, 2021).
From the calculation the mean value of selected expenditure is 22.1.
II. Calculation of Median value
To get the value of media two steps will be followed in sequence manner to get reliable and
relevant figure. The step one is associated with arranging data set in ascending order and then
second stem is applying required formula to reach conclusion.
Step 1: Setting data in ascending order
S. No. Month
s
Money incurred on
transportation expenses

1 Mar 5
2 Jan 11
3 May 11
4 Aug 11
5 Feb 12
6 Sept 23
7 Oct 27
8 July 34
9 June 42
10 April 45
Step 2: Executing formula
Median (M) Number of observations 10
M (10+1)/2 5.5
(12+23)/2 17.5
Discussion of median value:
From the evaluation it can articulated that the median for the specific chosen expenses is
average of 5th and 6th cell. The outcome is 17.5 which has been obtained by applying mentioned
formula (Deuflhard and Hohmann, 2021).
III. Determination of mode value
Months Money incurred on transportation expenses
Jan 11
Feb 12
Mar 5
April 45
May 11
2 Jan 11
3 May 11
4 Aug 11
5 Feb 12
6 Sept 23
7 Oct 27
8 July 34
9 June 42
10 April 45
Step 2: Executing formula
Median (M) Number of observations 10
M (10+1)/2 5.5
(12+23)/2 17.5
Discussion of median value:
From the evaluation it can articulated that the median for the specific chosen expenses is
average of 5th and 6th cell. The outcome is 17.5 which has been obtained by applying mentioned
formula (Deuflhard and Hohmann, 2021).
III. Determination of mode value
Months Money incurred on transportation expenses
Jan 11
Feb 12
Mar 5
April 45
May 11
June 42
July 34
Aug 11
Sept 23
Oct 27
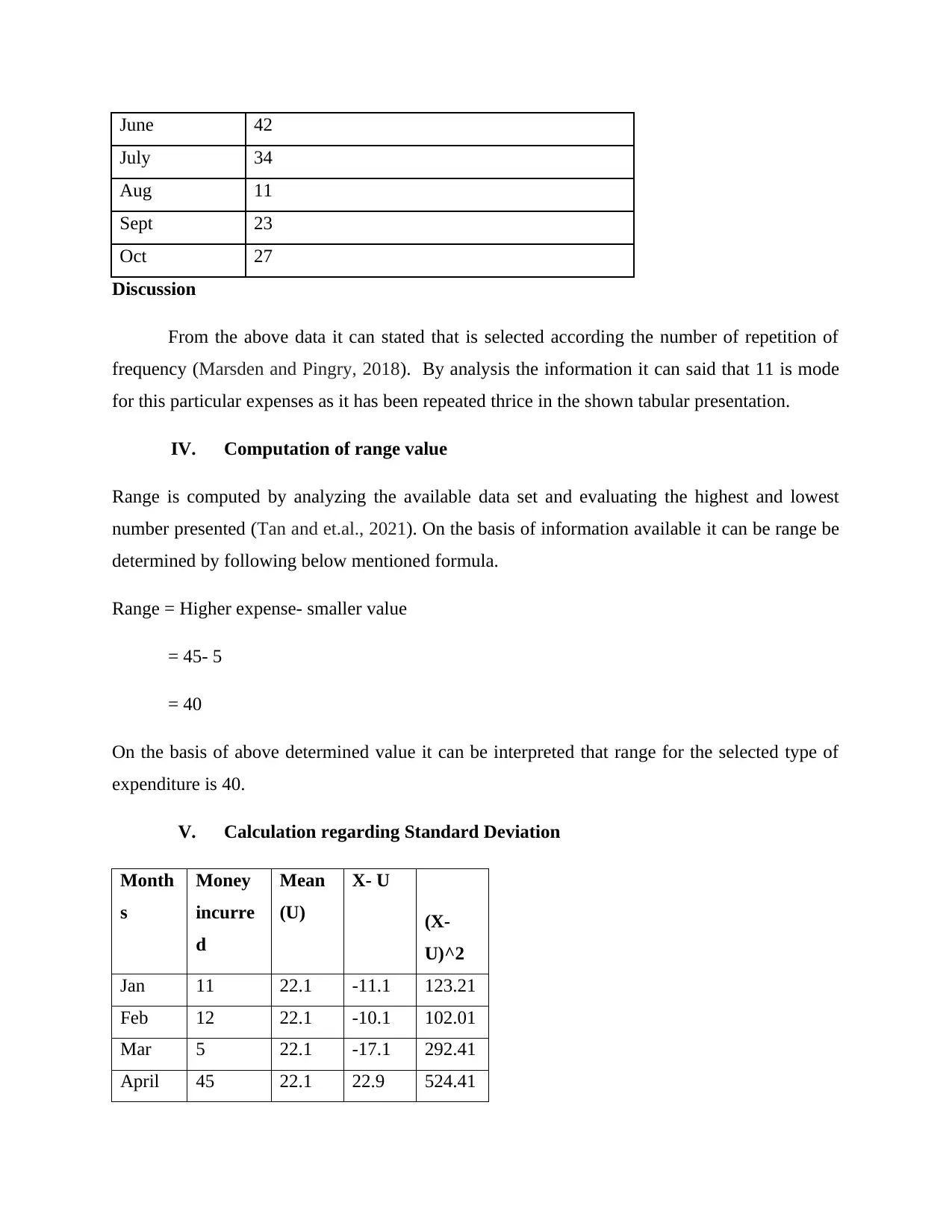
Discussion
From the above data it can stated that is selected according the number of repetition of
frequency (Marsden and Pingry, 2018). By analysis the information it can said that 11 is mode
for this particular expenses as it has been repeated thrice in the shown tabular presentation.
IV. Computation of range value
Range is computed by analyzing the available data set and evaluating the highest and lowest
number presented (Tan and et.al., 2021). On the basis of information available it can be range be
determined by following below mentioned formula.
Range = Higher expense- smaller value
= 45- 5
= 40
On the basis of above determined value it can be interpreted that range for the selected type of
expenditure is 40.
V. Calculation regarding Standard Deviation
Month
s
Money
incurre
d
Mean
(U)
X- U
(X-
U)^2
Jan 11 22.1 -11.1 123.21
Feb 12 22.1 -10.1 102.01
Mar 5 22.1 -17.1 292.41
April 45 22.1 22.9 524.41
July 34
Aug 11
Sept 23
Oct 27
Discussion
From the above data it can stated that is selected according the number of repetition of
frequency (Marsden and Pingry, 2018). By analysis the information it can said that 11 is mode
for this particular expenses as it has been repeated thrice in the shown tabular presentation.
IV. Computation of range value
Range is computed by analyzing the available data set and evaluating the highest and lowest
number presented (Tan and et.al., 2021). On the basis of information available it can be range be
determined by following below mentioned formula.
Range = Higher expense- smaller value
= 45- 5
= 40
On the basis of above determined value it can be interpreted that range for the selected type of
expenditure is 40.
V. Calculation regarding Standard Deviation
Month
s
Money
incurre
d
Mean
(U)
X- U
(X-
U)^2
Jan 11 22.1 -11.1 123.21
Feb 12 22.1 -10.1 102.01
Mar 5 22.1 -17.1 292.41
April 45 22.1 22.9 524.41
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
May 11 22.1 -11.1 123.21
June 42 22.1 19.9 396.01
July 34 22.1 11.9 141.61
Aug 11 22.1 -11.1 123.21
Sept 23 22.1 0.9 0.81
Oct 27 22.1 4.9 24.01
Total
1850.9
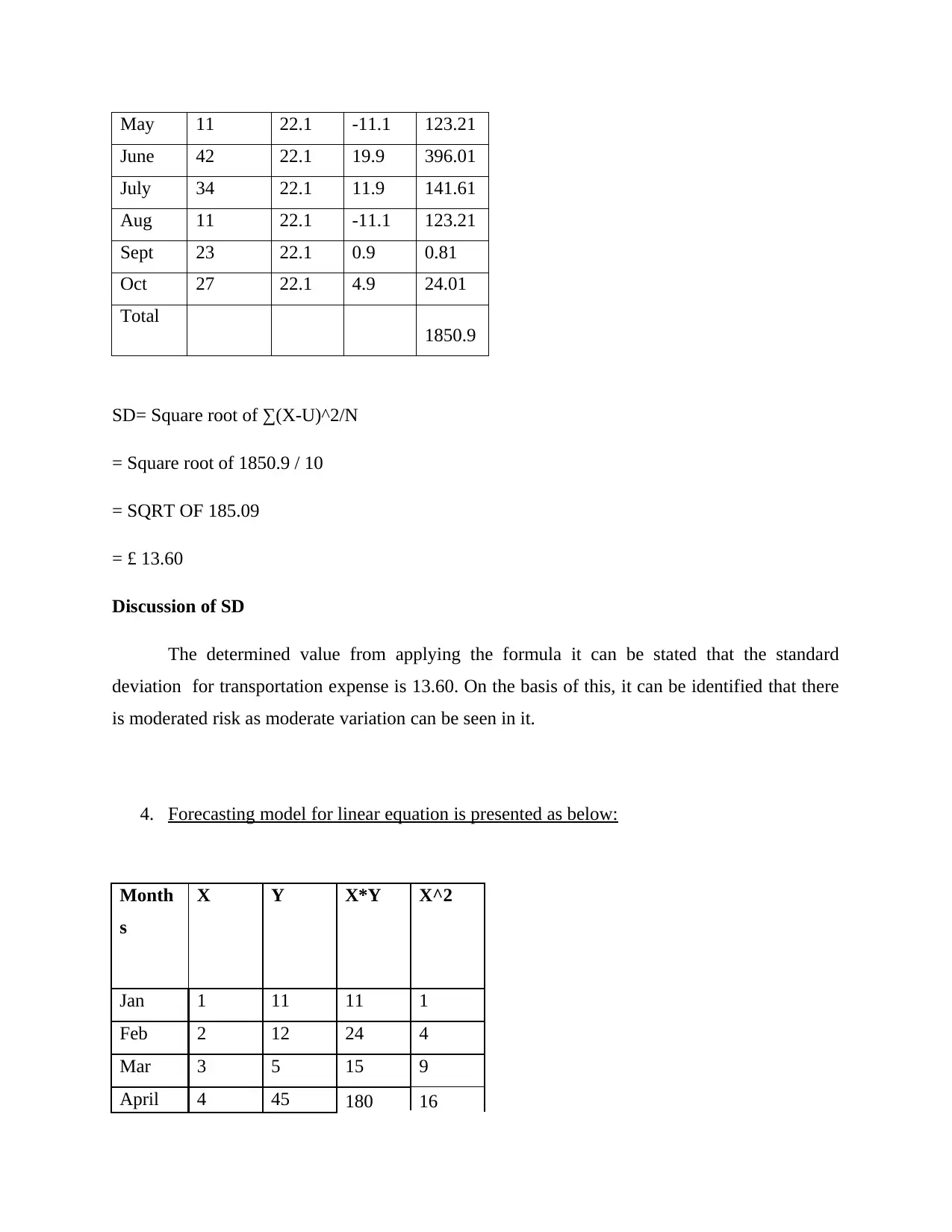
SD= Square root of ∑(X-U)^2/N
= Square root of 1850.9 / 10
= SQRT OF 185.09
= £ 13.60
Discussion of SD
The determined value from applying the formula it can be stated that the standard
deviation for transportation expense is 13.60. On the basis of this, it can be identified that there
is moderated risk as moderate variation can be seen in it.
4. Forecasting model for linear equation is presented as below:
Month
s
X Y X*Y X^2
Jan 1 11 11 1
Feb 2 12 24 4
Mar 3 5 15 9
April 4 45 180 16
June 42 22.1 19.9 396.01
July 34 22.1 11.9 141.61
Aug 11 22.1 -11.1 123.21
Sept 23 22.1 0.9 0.81
Oct 27 22.1 4.9 24.01
Total
1850.9
SD= Square root of ∑(X-U)^2/N
= Square root of 1850.9 / 10
= SQRT OF 185.09
= £ 13.60
Discussion of SD
The determined value from applying the formula it can be stated that the standard
deviation for transportation expense is 13.60. On the basis of this, it can be identified that there
is moderated risk as moderate variation can be seen in it.
4. Forecasting model for linear equation is presented as below:
Month
s
X Y X*Y X^2
Jan 1 11 11 1
Feb 2 12 24 4
Mar 3 5 15 9
April 4 45 180 16

May 5 11 55 25
June 6 42 252 36
July 7 34 238 49
Aug 8 11 88 64
Sept 9 23 207 81
Oct 10 27 270 100
Total 55 221 1340 385
i. Determination of m value:
m = Σxy – Σx Σy / Σ x^2 – (Σx)^2
= 1340-(55*221)/ 385- (55)^2
=(1340-12155) / (385-3025)
= -10815/-2640
= 4.09
ii. Computation of value c is illustrated below
C = Σy – m Σx / N
= 221 – (4.09*55)/10
= -0.35
iii. Showing computation of 12th and 14th day
Ascertainment of value in case of 12th
Y= mX +c
= 4.09(12) + (-0.35)
= 49.08 - 0.35
= £48.73
Determination in case of 14th
Y= mX +c
= 4.09(14) + (-0.35)
June 6 42 252 36
July 7 34 238 49
Aug 8 11 88 64
Sept 9 23 207 81
Oct 10 27 270 100
Total 55 221 1340 385
i. Determination of m value:
m = Σxy – Σx Σy / Σ x^2 – (Σx)^2
= 1340-(55*221)/ 385- (55)^2
=(1340-12155) / (385-3025)
= -10815/-2640
= 4.09
ii. Computation of value c is illustrated below
C = Σy – m Σx / N
= 221 – (4.09*55)/10
= -0.35
iii. Showing computation of 12th and 14th day
Ascertainment of value in case of 12th
Y= mX +c
= 4.09(12) + (-0.35)
= 49.08 - 0.35
= £48.73
Determination in case of 14th
Y= mX +c
= 4.09(14) + (-0.35)

= 57.26 + (-0.35)
= 57.26 - 0.35
= £56.91
Discussion
From the above illustrated calculation it can be said that value of m and c obtained are
4.09 and (-0.35). In order to get these values the given formula has been taken into consideration.
On the basis of this values of 12th and 14th day are calculated by substituting m and c’s value
which has given outcome 48.73 and £56.91.
CONCLUSION
From the above report it can be summarized that numerical and data analysis plays
significant role in current scenario to provide appropriate evaluation so that strategic decision
can be taken. The present report has given emphasis on pictorial and tabular reflection of
selected data set. In addition to this, practical exposure regarding mean, mode, median, range and
SD can been seen in report. Case study has presented forecasting of linear equation to obtain m
and c’s values to fulfill the objective of current report to ascertain the expenditure regarding
mentioned period.
1.
= 57.26 - 0.35
= £56.91
Discussion
From the above illustrated calculation it can be said that value of m and c obtained are
4.09 and (-0.35). In order to get these values the given formula has been taken into consideration.
On the basis of this values of 12th and 14th day are calculated by substituting m and c’s value
which has given outcome 48.73 and £56.91.
CONCLUSION
From the above report it can be summarized that numerical and data analysis plays
significant role in current scenario to provide appropriate evaluation so that strategic decision
can be taken. The present report has given emphasis on pictorial and tabular reflection of
selected data set. In addition to this, practical exposure regarding mean, mode, median, range and
SD can been seen in report. Case study has presented forecasting of linear equation to obtain m
and c’s values to fulfill the objective of current report to ascertain the expenditure regarding
mentioned period.
1.
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

REFERENCES
Books and Journals
Marsden, J. R. and Pingry, D. E., 2018. Numerical data quality in IS research and the
implications for replication. Decision Support Systems. 115. pp.A1-A7.
Tan, X. and et.al., 2021. The impact of uneven temperature distribution on stability of concrete
structures using data analysis and numerical approach. Advances in
Structural Engineering. 24(2). pp.279-290.
Deuflhard, P. and Hohmann, A., 2021. Numerical analysis. de Gruyter.
Gill, P. E., Murray, W. and Wright, M. H., 2021. Numerical linear algebra and optimization.
Society for Industrial and Applied Mathematics.
Books and Journals
Marsden, J. R. and Pingry, D. E., 2018. Numerical data quality in IS research and the
implications for replication. Decision Support Systems. 115. pp.A1-A7.
Tan, X. and et.al., 2021. The impact of uneven temperature distribution on stability of concrete
structures using data analysis and numerical approach. Advances in
Structural Engineering. 24(2). pp.279-290.
Deuflhard, P. and Hohmann, A., 2021. Numerical analysis. de Gruyter.
Gill, P. E., Murray, W. and Wright, M. H., 2021. Numerical linear algebra and optimization.
Society for Industrial and Applied Mathematics.
1 out of 11
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.





