Numeracy and Data Analysis

This report focuses on data analysis and its importance in retrieving useful information. It covers topics like data collection, calculations such as mean, mode, median, and forecasting. It also discusses linear forecasting models.

Numeracy and Data Analysis

Contents
INTRODUCTION.......................................................................................................................................3
MAIN BODY..............................................................................................................................................3
CONCLUSION.........................................................................................................................................10
REFERENCES..........................................................................................................................................11

INTRODUCTION
Data analysis is a retrieval and data gathering tool for us to obtain useful information. In
other terms, the analysis of data is essentially intended to analyze what data relies on perception,
whatever other data it tries to inform (Coben, Miller-Reilly, Satherley and Earle, 2016). The
report mostly deals with data collection, in which data is related to the sleeping hours on
different days. As per the project study, significant calculation areas are also carried out, such as
mean, mode, medium and forecasting.
MAIN BODY
1. Arrangement of the data in a table format.
Day Sleeping hours
1 9
2 10
3 12
4 8
5 7
6 9
7 8
8 7
9 9
10 12
2. Presentation of the data using any two types of charts.
Column chart- A column diagram is a visual picture in which each section reflects the
row height, relative to the values displayed (Bokhari, Rashid and Chan, 2016). Column
screens are generally recognized as vertical bar tables.

1 2 3 4 5 6 7 8 9 10
0
2
4
6
8
10
12
14
9
10
12
8
7
9
8
7
9
12
Sleeping hours
Sleeping hours
Bar chart- A bar chart or bar map is a diagram of categorical data that is directly proportional to
its height or width, or linear lines (Nogueira, Thai, Nelson, 2016). The bars are vertical or
horizontal.
1
2
3
4
5
6
7
8
9
10
0 2 4 6 8 10 12 14
9
10
12
8
7
9
8
7
9
12
Sleeping hours
Sleeping hours
3. Calculation of followings:

Mean- The more common term for a mean is the average number of all parameters, which can
be described as a statistical sampling of a single random variable (Shalley and Stewart, 2017).
Add and split the values of a word in a variety of terms to determine this. The average value is
calculated below of sleeping hours is as follows:
Day Sleeping hours
1 9
2 10
3 12
4 8
5 7
6 9
7 8
8 7
9 9
10 12
Total 91
Mean= Sum of all values/number of values
= 91/10
= 9.1
Mode- It is considered as mode by the most popular variable in a group of data (Vignoles,
2016). The mode value is determined below of sleeping hours of 10 days:
Day Sleeping hours
1 9
2 10
3 12
4 8
5 7

6 9
7 8
8 7
9 9
10 12
Total 91
The value of mode is 9 because frequency of this term is higher among all data. Thus mode is 9.
Median- The median is the middle value of the set of numbers where no number is replicated and
no array variable occurs. In other words, median is the sum of the upper half from the lower half
of a survey, a group or a statistical distribution in probability and statistics theory (Estrada-Mejia,
De Vries and Zeelenberg, 2016). It can be known to be the "upper" attribute for a data collection.
The following is determined by a formula:
When data set is odd= (N+1)/2th item.
When data set is even= {N/2th item+ N/2th item + 1}2
In the above mentioned data set, this can be found out that data set is even so median will be
calculated as follows:
First of all, the data set needs to be arranged in ascending order:
Day Sleeping hours
1 7
2 7
3 8
4 8
5 9
6 9
7 9
8 10
9 12

10 12
N= 10
M= (10/2th item + 10/2th item + 1)/2
= (5th item+ 6th item)/2
= (9+9)/2
= 9
Range- The gap between higher and lower value is defined as range. In other words, the selection
of data between the largest and least values of statistics is the distinction (Ballarini and Sloman,
2017). The distinction is unique, because the width of a collection of data is extracted from the
smallest meaning. The definition of distribution, though, has a more nuanced sense in descriptive
statistics The range value of the abovementioned data collection is determined in such a way:
Higher value= 12
Lower value= 7
Range= (12-7)
= 5
Standard deviation- This is a statistical measurement of the distribution of medium or predicted
values to the population (Gatobu, Arocha and Hoffman-Goetz, 2016). Many forecasts are
incorrectly predicted to be below normal. The figures are more commonly represented by a large
norm disparity. The calculation is as follows:
Day Sleeping
hours
x-m (x-m) 2
1 9 -0.1 0.01
2 10 0.9 0.81
3 12 2.9 8.41
4 8 -1.1 1.21

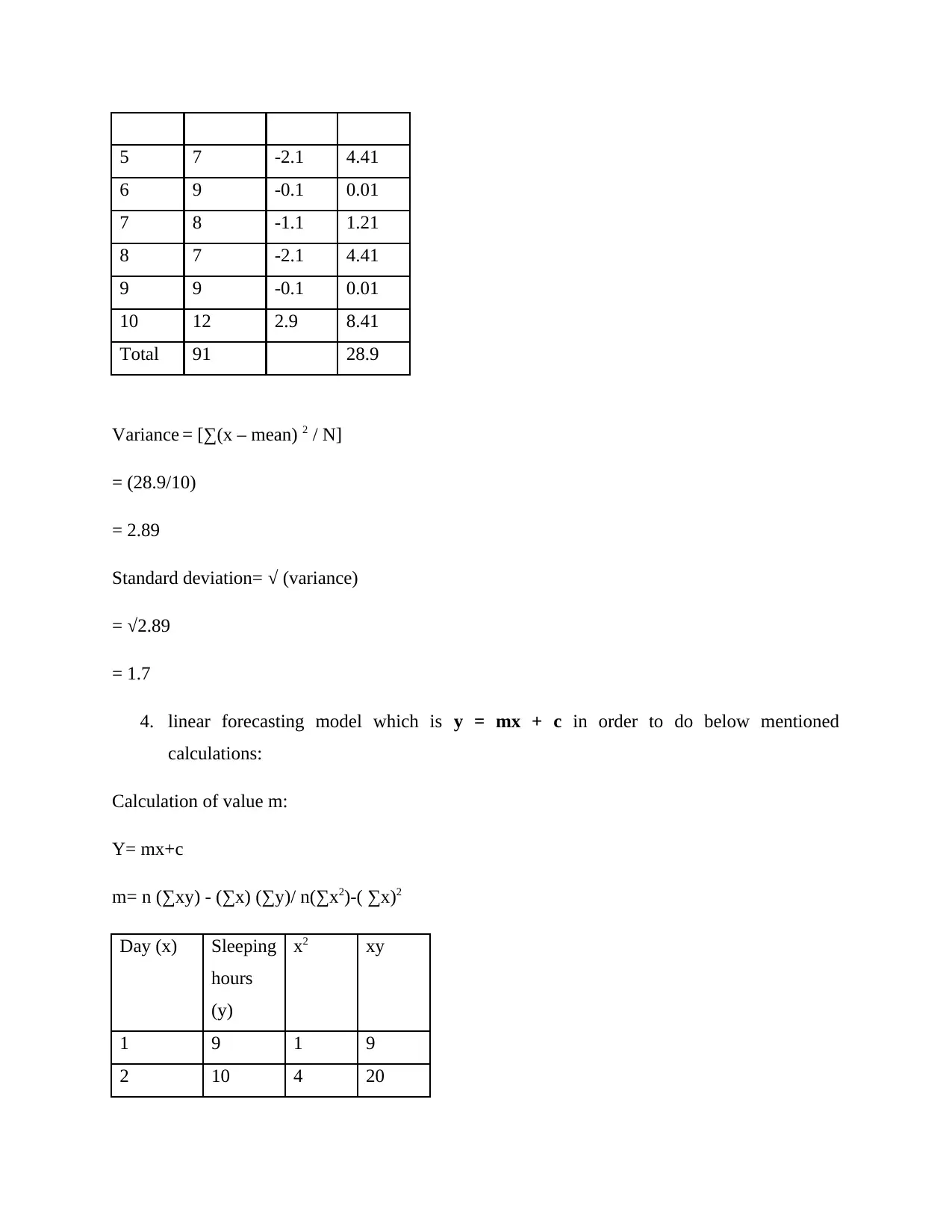
5 7 -2.1 4.41
6 9 -0.1 0.01
7 8 -1.1 1.21
8 7 -2.1 4.41
9 9 -0.1 0.01
10 12 2.9 8.41
Total 91 28.9
Variance = [∑(x – mean) 2 / N]
= (28.9/10)
= 2.89
Standard deviation= √ (variance)
= √2.89
= 1.7
4. linear forecasting model which is y = mx + c in order to do below mentioned
calculations:
Calculation of value m:
Y= mx+c
m= n (∑xy) - (∑x) (∑y)/ n(∑x2)-( ∑x)2
Day (x) Sleeping
hours
(y)
x2 xy
1 9 1 9
2 10 4 20

3 12 9 36
4 8 16 32
5 7 25 35
6 9 36 54
7 8 49 56
8 7 64 56
9 9 81 81
10 12 100 120
55 91 385 499
= 10(499) - (55)*(91)/10(385)-(55) 2
= 4990-5005/3850-3025
= -15/825
= -0.018
Calculation of c:
c= [(∑y) / n]-m (∑x/n)
= [91/10] - (-0.018)(55/10)
= 9.1-(-0.099)
= 9.19
Forecasting for 11 and 15 days:
Forecasting for day 11:
y= mx+c
= -0.018*11+9.19

= -0.20+9.19
= 8.99 or 9 hours
Forecasting for day 15:
= -0.018*15+9.19
= -0.27+9.19
= 8.92 hours
CONCLUSION
It is stated in the aforementioned report that data analysis is too important to classify any
specific effects of data collection. In this report, different values such as average, mode, median
and several others have been determined. The second part of the report concludes with a linear
equation of the forecasts of sleeping hours for day 11 and day 15.

REFERENCES
Books and journal:
Gatobu, S.K., Arocha, J.F. and Hoffman-Goetz, L., 2016. Numeracy, health numeracy, and older
immigrants’ primary language: an observation-oriented exploration. Basic and Applied
Social Psychology, 38(4), pp.185-199.
Ballarini, C. and Sloman, S.A., 2017. Reasons and the “Motivated Numeracy Effect.”.
In Proceedings of the 39th annual meeting of the Cognitive Science Society (pp. 1580-
1585).
Estrada-Mejia, C., De Vries, M. and Zeelenberg, M., 2016. Numeracy and wealth. Journal of
Economic Psychology, 54, pp.53-63.
Vignoles, A., 2016. What is the economic value of literacy and numeracy?. IZA World of Labor.
Shalley, F. and Stewart, A., 2017. Aboriginal adult English language literacy and numeracy in
the Northern Territory: A statistical overview. Charles Darwin University.
Nogueira, L.M., Thai, C.L., Nelson, W. and Oh, A., 2016. Nutrition label numeracy: Disparities
and association with health behaviors. American journal of health behavior, 40(4),
pp.427-436.
Coben, D., Miller-Reilly, B., Satherley, P. and Earle, D., 2016. Making the most of PIAAC:
Preliminary investigation of adults’ numeracy practices through secondary analysis of the
PIAAC dataset.
Bokhari, R., Rashid, S.M. and Chan, S.H., 2016. Teachers’ Perception on the Implementation of
the Literacy, Numeracy and Screening (LINUS LBI 2.0) Programme among Lower
Primary ESL Pupils. Malaysian Journal of ELT Research, 11(1), p.14.