Statistical Analysis of Train Station Usage

This assignment involves analyzing data on train station usage in Chelmsford for the past 10 years, and using statistical methods to forecast usage for 12 and 15 years. The report includes calculations of the value of 'm' and 'c' in a linear forecasting equation, as well as other statistical tools. It concludes that correct analysis of data can assist companies and investors in decision-making related to investment.

)
Numeracy and Data Analysis

Table of Contents
INTRODUCTION..................................................................................................................................3
MAIN BODY.........................................................................................................................................3
1. Arranging data in table form.........................................................................................................3
2. Presentation of data in graph form................................................................................................3
3. Steps for calculating the values of following methods..................................................................5
4. Explaining following.....................................................................................................................6
1. Steps for calculating value of “m”.................................................................................................6
2.Steps for calculating value of “c”...................................................................................................6
3. Forecasting for 12 & 15 years.......................................................................................................6
CONCLUSION......................................................................................................................................8
REFERENCES.......................................................................................................................................9

INTRODUCTION
Numeracy and Data analysis in statistics has to been done in an accurate and correct manner so that it
can assist every business organisation as well as individual in making their investment decision.
With the help of statistical formula, data has to be calculated properly for the given relevant time
period. Analysis of data made are enclosed in the financial statements of the company which
provides detailed interpretation to investors. With the help of financial statements, a company is able
to depicts its true and fair financial position. The present report is based on train station usage of
Chelmsford, UK. Report will provide detail about train station usage for the last 10 years from 2009
to 2018. It will disclose presentation of data with the help of graph and its interpretation. Further, it
will enclose steps for calculating various statistical tools and linear forecasting equation.
MAIN BODY
1. Arranging data in table form.
Year Train Station usage
data (in 000)
2009-10 227
2010-11 41
2011-12 51
2012-13 249
2013-14 254
2014-15 263
2015-16 278
2016-17 91
2017-18 208
2018-19 1672
(gov.uk, 2019)
Interpretation – From the above table it can be interpreted that over the time period of 10 years, the
total number of passengers who have entered, exited through the Chelmsford train station UK has
been depicting a mixed trend. The number of passengers using train station has increased from the
year 2009 to the year 2018. In 2010, only 41000 passengers has used train station for their purpose
which is the lowest among 10 year time period. With the increase in time, usage by passengers has
also increased to 1672000. It can be concluded that Chelmsford station is having a fluctuating trend
in case of train station usage.
2. Presentation of data in graph form.
Column graph - It is a form of Bar graph by use of which one can present information or data in bar
form (Rees, 2018). It makes use of vertical bars for the purpose of defining values as mentioned in
the given data set.

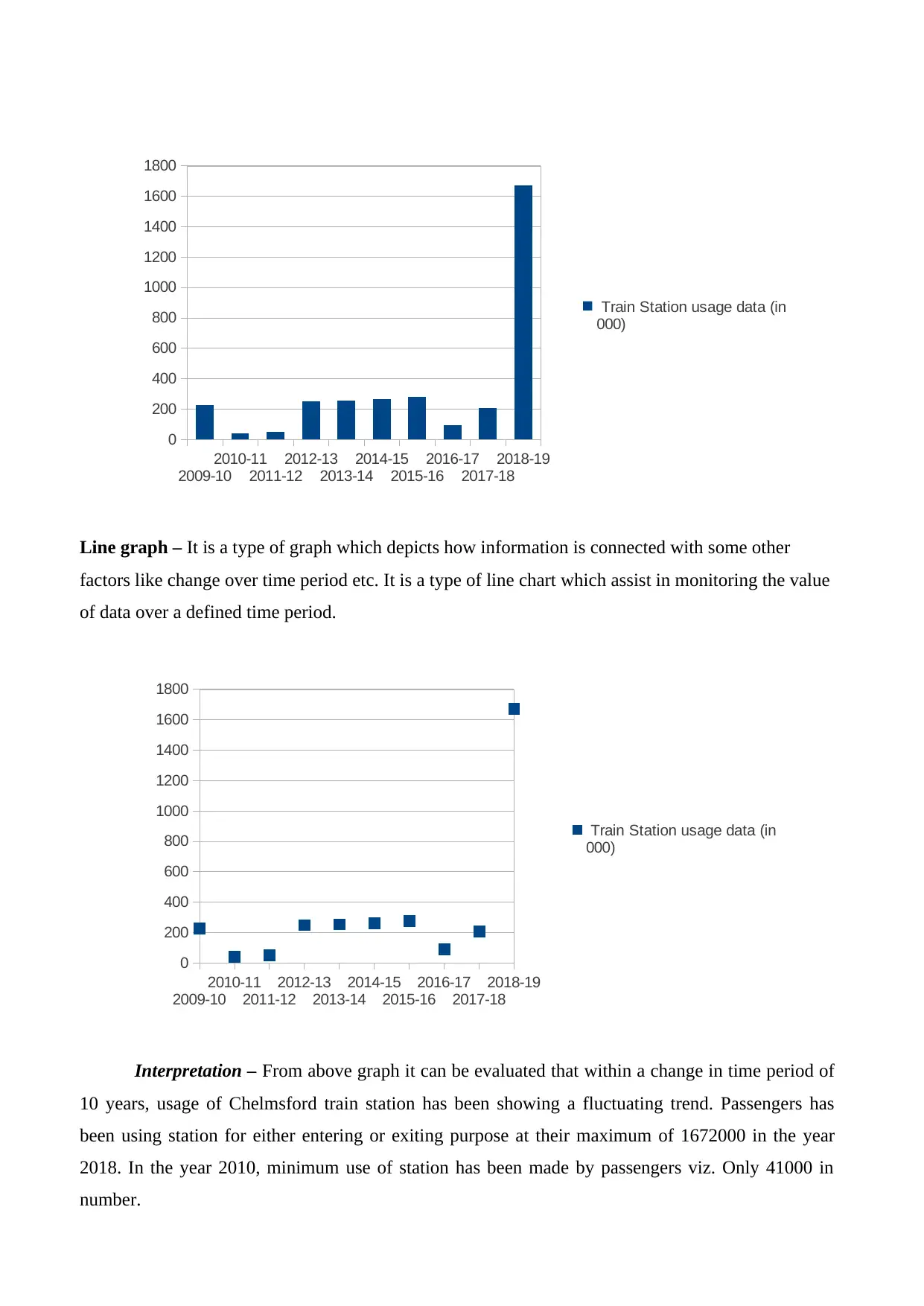
Line graph – It is a type of graph which depicts how information is connected with some other
factors like change over time period etc. It is a type of line chart which assist in monitoring the value
of data over a defined time period.
Interpretation – From above graph it can be evaluated that within a change in time period of
10 years, usage of Chelmsford train station has been showing a fluctuating trend. Passengers has
been using station for either entering or exiting purpose at their maximum of 1672000 in the year
2018. In the year 2010, minimum use of station has been made by passengers viz. Only 41000 in
number.
2009-10
2010-11
2011-12
2012-13
2013-14
2014-15
2015-16
2016-17
2017-18
2018-19
0
200
400
600
800
1000
1200
1400
1600
1800
Train Station usage data (in
000)
2009-10
2010-11
2011-12
2012-13
2013-14
2014-15
2015-16
2016-17
2017-18
2018-19
0
200
400
600
800
1000
1200
1400
1600
1800
Train Station usage data (in
000)

3. Steps for calculating the values of following methods.
For evaluating statistical values, proper and accurate statistical tools should be made in use so
that data and information can be analyzed and its interpretation can be made in correct manner.
Year Train Station usage
data (in 000)
2009-10 227
2010-11 41
2011-12 51
2012-13 249
2013-14 254
2014-15 263
2015-16 278
2016-17 91
2017-18 208
2018-19 1672
Mean 333.4
Median 238
Mode #N/A
Range 1631
Standard
Deviation 478.9
Following steps has to be followed:
1. Mean – Data values of which average to be calculated has to be determined. These values
can be of either small or big number (Ali and Bhaskar, 2016). Addition of all values in given
data set has to be done together. After adding up all it is divided by the numbers in question.
2. Median – For determining median, all the data value or numbers given has to be arrange in
ascending order or starting from least to the greatest number. Find the mean of two numbers
which is falling in the middle. It will be median.
3. Mode - Mention all the number of the given data set and arrange numbers ranging from the
smallest to the largest as per their series. Count the number of time each number is occurring.
The value which is repeating most of the time is required to be identified and will be modal
value.
4. Range - For determining the value of range, all numbers in given data set has to be list down.
Then numbers has to be arrange as per the order. The highest and lowest value number has to
be identified. After ascertaining the lowest and highest value number from the given data set,
subtraction is done. The smallest value of data set is subtracted from the largest value & will
give range value (Luo & et.al., 2018).

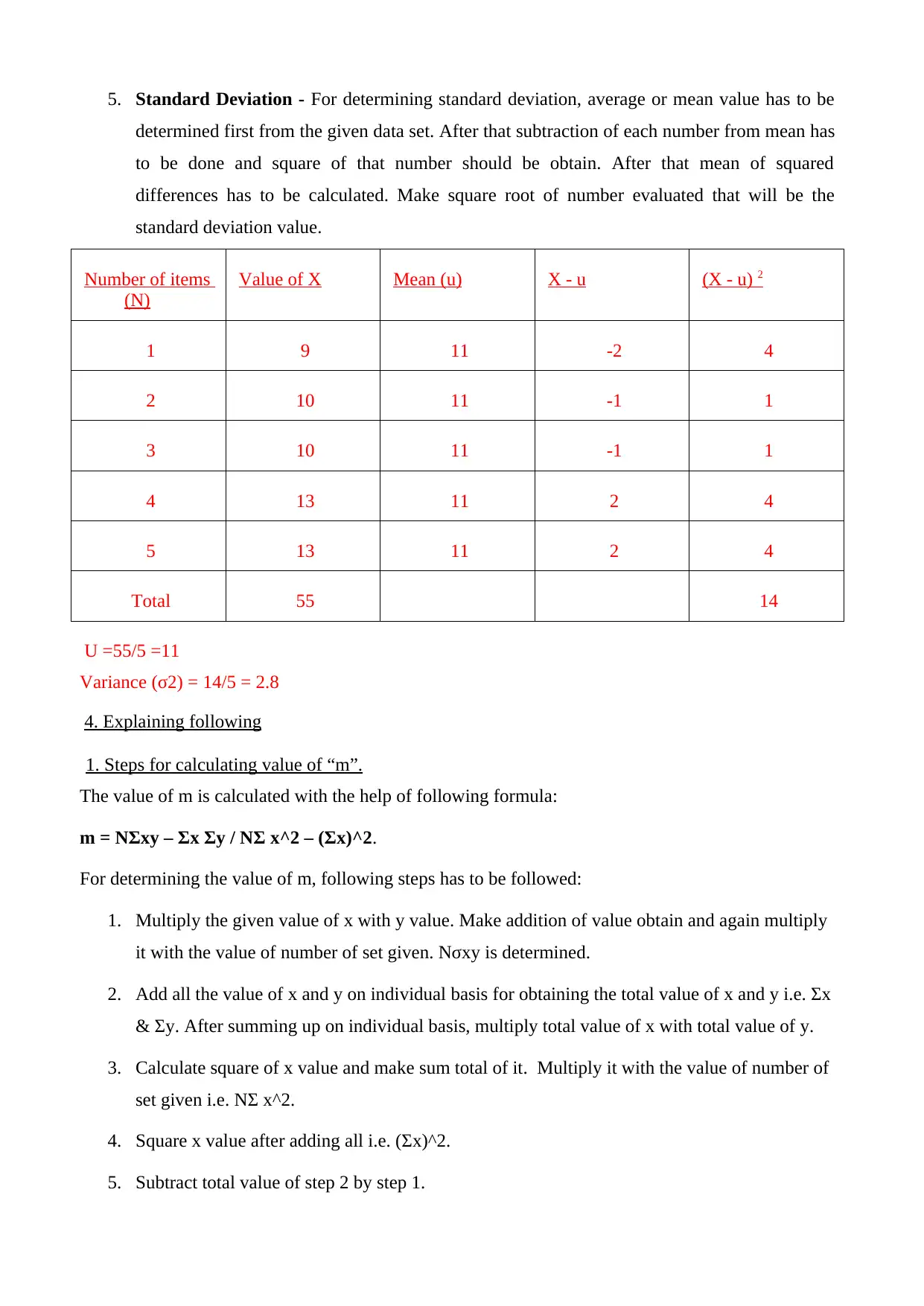
5. Standard Deviation - For determining standard deviation, average or mean value has to be
determined first from the given data set. After that subtraction of each number from mean has
to be done and square of that number should be obtain. After that mean of squared
differences has to be calculated. Make square root of number evaluated that will be the
standard deviation value.
Number of items
(N)
Value of X Mean (u) X - u (X - u) 2
1 9 11 -2 4
2 10 11 -1 1
3 10 11 -1 1
4 13 11 2 4
5 13 11 2 4
Total 55 14
U =55/5 =11
Variance (σ2) = 14/5 = 2.8
4. Explaining following
1. Steps for calculating value of “m”.
The value of m is calculated with the help of following formula:
m = NΣxy – Σx Σy / NΣ x^2 – (Σx)^2.
For determining the value of m, following steps has to be followed:
1. Multiply the given value of x with y value. Make addition of value obtain and again multiply
it with the value of number of set given. Nσxy is determined.
2. Add all the value of x and y on individual basis for obtaining the total value of x and y i.e. Σx
& Σy. After summing up on individual basis, multiply total value of x with total value of y.
3. Calculate square of x value and make sum total of it. Multiply it with the value of number of
set given i.e. NΣ x^2.
4. Square x value after adding all i.e. (Σx)^2.
5. Subtract total value of step 2 by step 1.

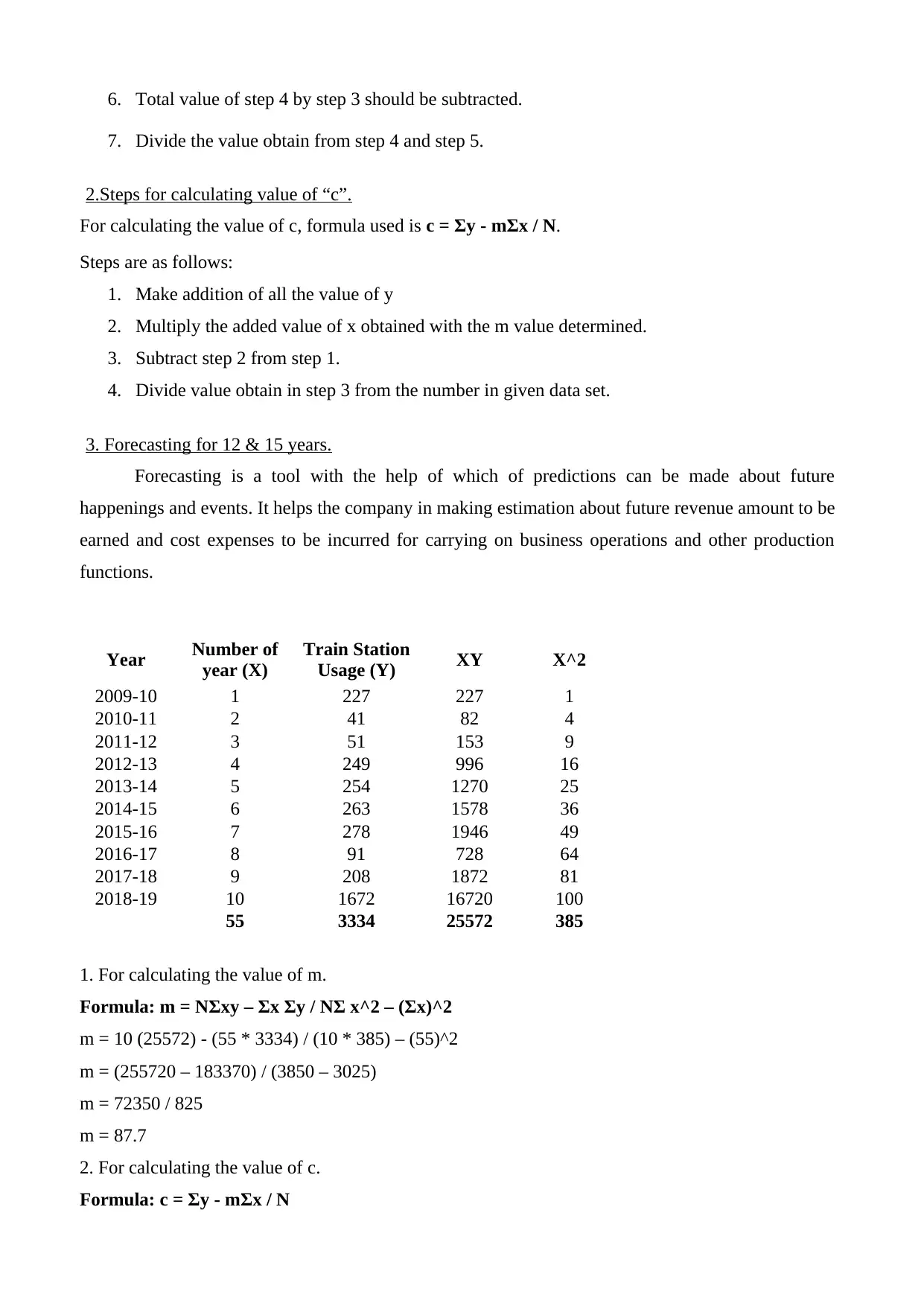
6. Total value of step 4 by step 3 should be subtracted.
7. Divide the value obtain from step 4 and step 5.
2.Steps for calculating value of “c”.
For calculating the value of c, formula used is c = Σy - mΣx / N.
Steps are as follows:
1. Make addition of all the value of y
2. Multiply the added value of x obtained with the m value determined.
3. Subtract step 2 from step 1.
4. Divide value obtain in step 3 from the number in given data set.
3. Forecasting for 12 & 15 years.
Forecasting is a tool with the help of which of predictions can be made about future
happenings and events. It helps the company in making estimation about future revenue amount to be
earned and cost expenses to be incurred for carrying on business operations and other production
functions.
Year Number of
year (X)
Train Station
Usage (Y) XY X^2
2009-10 1 227 227 1
2010-11 2 41 82 4
2011-12 3 51 153 9
2012-13 4 249 996 16
2013-14 5 254 1270 25
2014-15 6 263 1578 36
2015-16 7 278 1946 49
2016-17 8 91 728 64
2017-18 9 208 1872 81
2018-19 10 1672 16720 100
55 3334 25572 385
1. For calculating the value of m.
Formula: m = NΣxy – Σx Σy / NΣ x^2 – (Σx)^2
m = 10 (25572) - (55 * 3334) / (10 * 385) – (55)^2
m = (255720 – 183370) / (3850 – 3025)
m = 72350 / 825
m = 87.7
2. For calculating the value of c.
Formula: c = Σy - mΣx / N

c = 3334 – ((87.7 * 55) / 10)
c = (3334 – 482.35)
c = 2851.7
Forecasting station
usage (in years) Y = mX + c
12
Here x = 12 Years
Y = 87.7 (12) +
Y =1052.4 + 2851.7
Y = 3904.1
15
Here x = 15 Years
Y = 87.7 (15) +
Y =1315.5 + 2851.7
Y = 4167.2
CONCLUSION
From the above report it can be concluded that by having correct analysis of statistical as well
financial data and information, it can assist company and investors in decision making related to
investment. The report has defined that how passengers has make use of Chelmsford train station in
form of entering and exiting for the last 10 year time period. Also, report has discloses various steps
which has to be taken for determining the value of m and c in a linear forecasting equation & also of
different statistical tools.

REFERENCES
Books and Journals
Ali, Z. and Bhaskar, S. B., 2016. Basic statistical tools in research and data analysis. Indian journal
of anaesthesia. 60(9). p.662.
Luo, D. and et.al., 2018. Optimally estimating the sample mean from the sample size, median, mid-
range, and/or mid-quartile range. Statistical methods in medical research. 27(6). pp.1785-1805.
Rees, D. G., 2018. Essential statistics. Chapman and Hall/CRC.
Salkind, N. J., 2016. Statistics for people who (think they) hate statistics. Sage publications.
Online
Bar graphs meaning. 2018. [Online]. Available through: <https://www.mathsisfun.com/data/bar-
graphs.html>.
Gov.uk. 2019. Train usage data. [Online]. Available through:
<http://data.london.gov.uk/dataset/train-station-usage>.