Numeracy and Data Analysis
VerifiedAdded on 2022/12/28
|11
|1528
|59
AI Summary
This document discusses numeracy and data analysis, covering topics such as arranging data in table format, presenting data with charts, calculating mean, mode, median, range, and standard deviation, and using linear forecasting models. It also provides examples and explanations for each concept. The document is relevant for students studying data analysis or anyone interested in understanding and applying statistical concepts.
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

Numeracy and Data Analysis
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

Contents
INTRODUCTION...........................................................................................................................3
MAIN BODY..................................................................................................................................3
1. Arranging chosen data of expenses in table format:...............................................................3
2. Presenting selected data of expenses with help of two different charts:.................................3
3. Calculate and discuss the followings:......................................................................................5
4. Linear forecasting model which is y = mx + c:.......................................................................8
CONCLUSION..............................................................................................................................10
REFERENCES..............................................................................................................................11
INTRODUCTION...........................................................................................................................3
MAIN BODY..................................................................................................................................3
1. Arranging chosen data of expenses in table format:...............................................................3
2. Presenting selected data of expenses with help of two different charts:.................................3
3. Calculate and discuss the followings:......................................................................................5
4. Linear forecasting model which is y = mx + c:.......................................................................8
CONCLUSION..............................................................................................................................10
REFERENCES..............................................................................................................................11
INTRODUCTION
Small, firms retail firms, in healthcare, and also in the field of sports utilizing data
analysis. This is a language that is global and more relevant than it has ever been. It sounds like
an advanced theory, but the study of knowledge is only just few concepts put into operation. The
procedure of analyzing data utilizing analytical or mathematical methods to discover valuable
information is regarded as data analysis (Kamilaris, Kartakoullis and Prenafeta-Boldú, 2017).
The study-assessment covers multiple concepts related to data analysis like standard deviation,
mean method, mode value, median etc. of data of monthly expenses for 10 sequential months.
Further, the study consists of linear forecasting model to make forecast of month 11 and month
12 expenses.
MAIN BODY
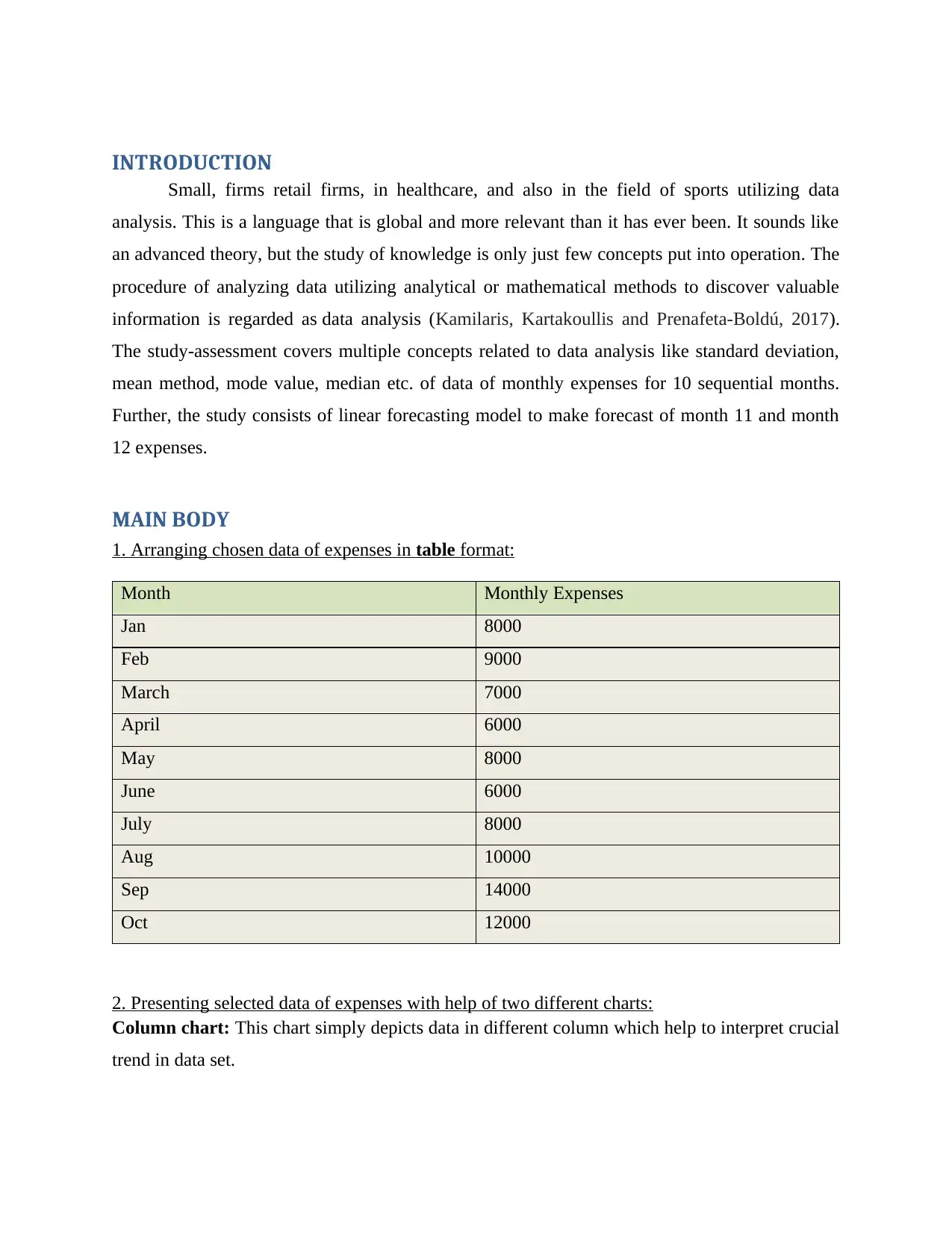
1. Arranging chosen data of expenses in table format:
Month Monthly Expenses
Jan 8000
Feb 9000
March 7000
April 6000
May 8000
June 6000
July 8000
Aug 10000
Sep 14000
Oct 12000
2. Presenting selected data of expenses with help of two different charts:
Column chart: This chart simply depicts data in different column which help to interpret crucial
trend in data set.
Small, firms retail firms, in healthcare, and also in the field of sports utilizing data
analysis. This is a language that is global and more relevant than it has ever been. It sounds like
an advanced theory, but the study of knowledge is only just few concepts put into operation. The
procedure of analyzing data utilizing analytical or mathematical methods to discover valuable
information is regarded as data analysis (Kamilaris, Kartakoullis and Prenafeta-Boldú, 2017).
The study-assessment covers multiple concepts related to data analysis like standard deviation,
mean method, mode value, median etc. of data of monthly expenses for 10 sequential months.
Further, the study consists of linear forecasting model to make forecast of month 11 and month
12 expenses.
MAIN BODY
1. Arranging chosen data of expenses in table format:
Month Monthly Expenses
Jan 8000
Feb 9000
March 7000
April 6000
May 8000
June 6000
July 8000
Aug 10000
Sep 14000
Oct 12000
2. Presenting selected data of expenses with help of two different charts:
Column chart: This chart simply depicts data in different column which help to interpret crucial
trend in data set.
Jan Feb March April May June July Aug Sep
0
2000
4000
6000
8000
10000
12000
14000
16000
8000
9000
7000
6000
8000
6000
8000
10000
14000
Monthly Expenses
Monthly Expenses
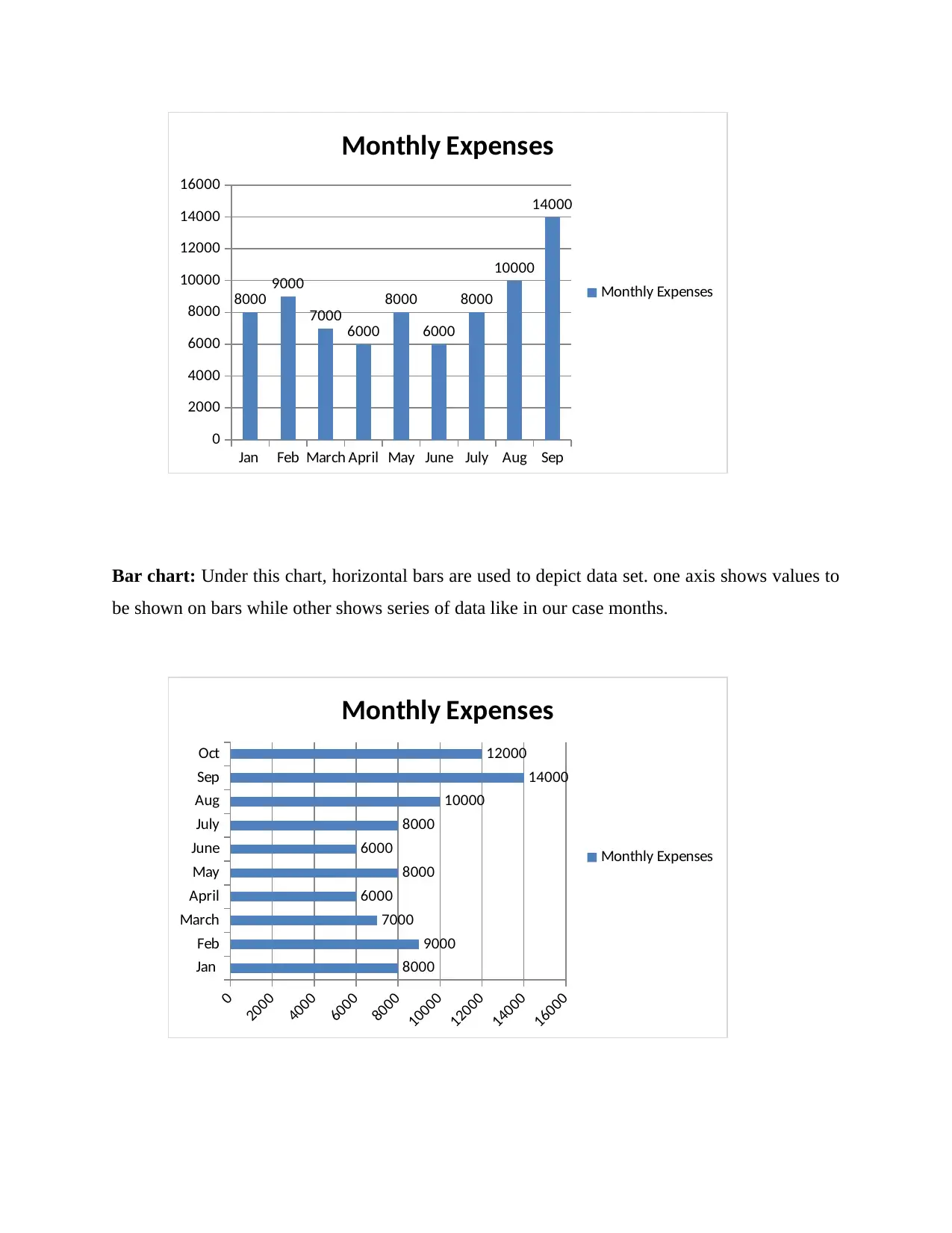
Bar chart: Under this chart, horizontal bars are used to depict data set. one axis shows values to
be shown on bars while other shows series of data like in our case months.
Jan
Feb
March
April
May
June
July
Aug
Sep
Oct
0
2000
4000
6000
8000
10000
12000
14000
16000
8000
9000
7000
6000
8000
6000
8000
10000
14000
12000
Monthly Expenses
Monthly Expenses
0
2000
4000
6000
8000
10000
12000
14000
16000
8000
9000
7000
6000
8000
6000
8000
10000
14000
Monthly Expenses
Monthly Expenses
Bar chart: Under this chart, horizontal bars are used to depict data set. one axis shows values to
be shown on bars while other shows series of data like in our case months.
Jan
Feb
March
April
May
June
July
Aug
Sep
Oct
0
2000
4000
6000
8000
10000
12000
14000
16000
8000
9000
7000
6000
8000
6000
8000
10000
14000
12000
Monthly Expenses
Monthly Expenses
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
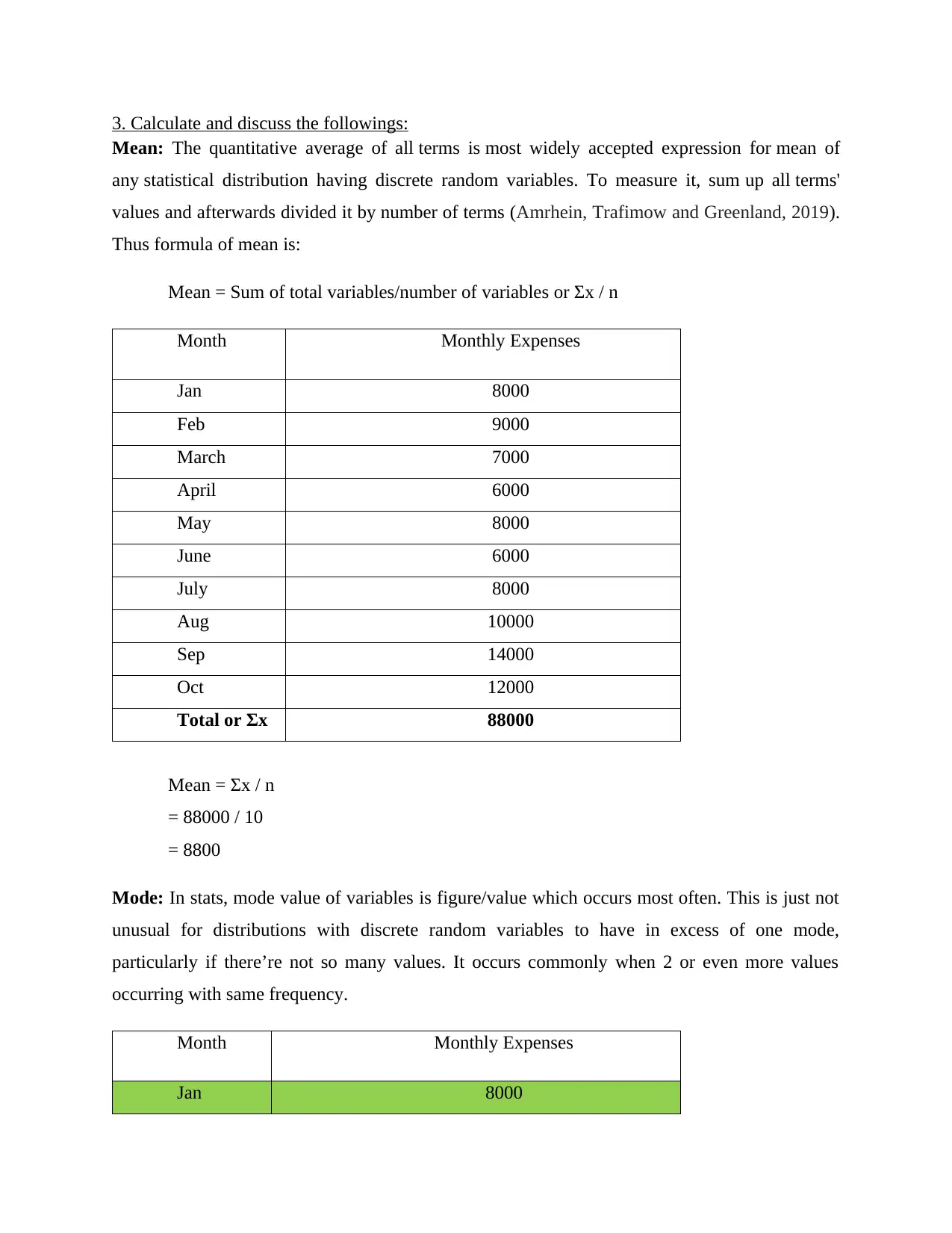
3. Calculate and discuss the followings:
Mean: The quantitative average of all terms is most widely accepted expression for mean of
any statistical distribution having discrete random variables. To measure it, sum up all terms'
values and afterwards divided it by number of terms (Amrhein, Trafimow and Greenland, 2019).
Thus formula of mean is:
Mean = Sum of total variables/number of variables or Σx / n
Month Monthly Expenses
Jan 8000
Feb 9000
March 7000
April 6000
May 8000
June 6000
July 8000
Aug 10000
Sep 14000
Oct 12000
Total or Σx 88000
Mean = Σx / n
= 88000 / 10
= 8800
Mode: In stats, mode value of variables is figure/value which occurs most often. This is just not
unusual for distributions with discrete random variables to have in excess of one mode,
particularly if there’re not so many values. It occurs commonly when 2 or even more values
occurring with same frequency.
Month Monthly Expenses
Jan 8000
Mean: The quantitative average of all terms is most widely accepted expression for mean of
any statistical distribution having discrete random variables. To measure it, sum up all terms'
values and afterwards divided it by number of terms (Amrhein, Trafimow and Greenland, 2019).
Thus formula of mean is:
Mean = Sum of total variables/number of variables or Σx / n
Month Monthly Expenses
Jan 8000
Feb 9000
March 7000
April 6000
May 8000
June 6000
July 8000
Aug 10000
Sep 14000
Oct 12000
Total or Σx 88000
Mean = Σx / n
= 88000 / 10
= 8800
Mode: In stats, mode value of variables is figure/value which occurs most often. This is just not
unusual for distributions with discrete random variables to have in excess of one mode,
particularly if there’re not so many values. It occurs commonly when 2 or even more values
occurring with same frequency.
Month Monthly Expenses
Jan 8000
Feb 9000
March 7000
April 6000
May 8000
June 6000
July 8000
Aug 10000
Sep 14000
Oct 12000
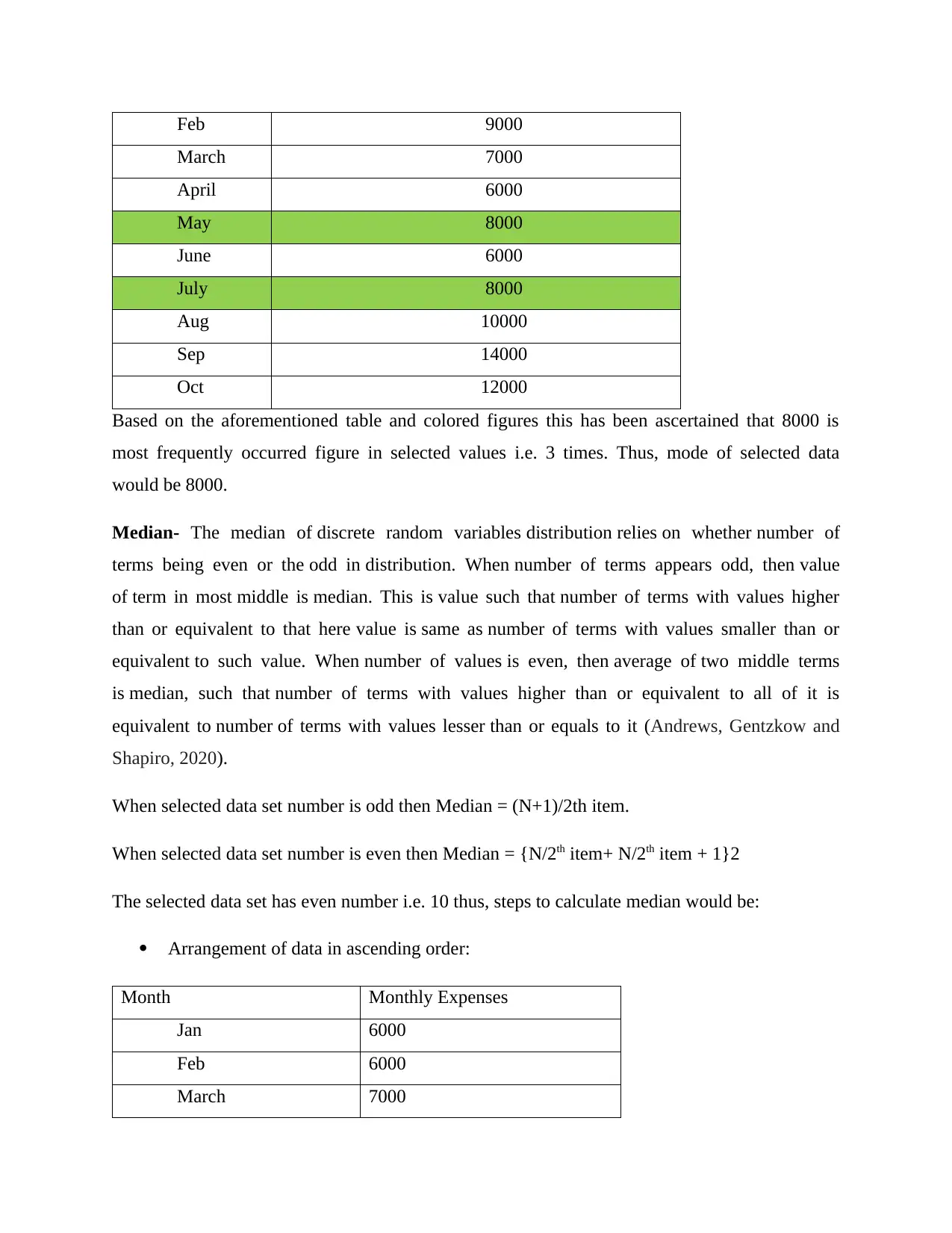
Based on the aforementioned table and colored figures this has been ascertained that 8000 is
most frequently occurred figure in selected values i.e. 3 times. Thus, mode of selected data
would be 8000.
Median- The median of discrete random variables distribution relies on whether number of
terms being even or the odd in distribution. When number of terms appears odd, then value
of term in most middle is median. This is value such that number of terms with values higher
than or equivalent to that here value is same as number of terms with values smaller than or
equivalent to such value. When number of values is even, then average of two middle terms
is median, such that number of terms with values higher than or equivalent to all of it is
equivalent to number of terms with values lesser than or equals to it (Andrews, Gentzkow and
Shapiro, 2020).
When selected data set number is odd then Median = (N+1)/2th item.
When selected data set number is even then Median = {N/2th item+ N/2th item + 1}2
The selected data set has even number i.e. 10 thus, steps to calculate median would be:
Arrangement of data in ascending order:
Month Monthly Expenses
Jan 6000
Feb 6000
March 7000
March 7000
April 6000
May 8000
June 6000
July 8000
Aug 10000
Sep 14000
Oct 12000
Based on the aforementioned table and colored figures this has been ascertained that 8000 is
most frequently occurred figure in selected values i.e. 3 times. Thus, mode of selected data
would be 8000.
Median- The median of discrete random variables distribution relies on whether number of
terms being even or the odd in distribution. When number of terms appears odd, then value
of term in most middle is median. This is value such that number of terms with values higher
than or equivalent to that here value is same as number of terms with values smaller than or
equivalent to such value. When number of values is even, then average of two middle terms
is median, such that number of terms with values higher than or equivalent to all of it is
equivalent to number of terms with values lesser than or equals to it (Andrews, Gentzkow and
Shapiro, 2020).
When selected data set number is odd then Median = (N+1)/2th item.
When selected data set number is even then Median = {N/2th item+ N/2th item + 1}2
The selected data set has even number i.e. 10 thus, steps to calculate median would be:
Arrangement of data in ascending order:
Month Monthly Expenses
Jan 6000
Feb 6000
March 7000

April 8000
May 8000
June 8000
July 9000
Aug 10000
Sep 12000
Oct 14000
N= 10
M= (10/2th item + 10/2th item + 1)/2
= (5th item+ 6th item)/2
= (8000 + 8000)/2
= 16000 / 2
= 8000
Range: The variance among the highest value as well as the lowest value is range of distribution
with discrete random variables. The range is simple difference between two extreme points
mostly on distribution slope for distribution with some constant random
variables where function's value drops to zero. The value of function is equivalent to 0 for value
outside of distribution range.
Higher value = 14000
Lower value = 6000
Range= (14000 - 6000)
= 8000
Standard deviation: This is kind of numerical value which is mainly applied to express how
widely values within data set vary. When data set vary highly from mean, then SD would be big
as well as vice-versa (Sharma, Kanchan and Krishan, 2018).
Month Expenses x- mean (x-
May 8000
June 8000
July 9000
Aug 10000
Sep 12000
Oct 14000
N= 10
M= (10/2th item + 10/2th item + 1)/2
= (5th item+ 6th item)/2
= (8000 + 8000)/2
= 16000 / 2
= 8000
Range: The variance among the highest value as well as the lowest value is range of distribution
with discrete random variables. The range is simple difference between two extreme points
mostly on distribution slope for distribution with some constant random
variables where function's value drops to zero. The value of function is equivalent to 0 for value
outside of distribution range.
Higher value = 14000
Lower value = 6000
Range= (14000 - 6000)
= 8000
Standard deviation: This is kind of numerical value which is mainly applied to express how
widely values within data set vary. When data set vary highly from mean, then SD would be big
as well as vice-versa (Sharma, Kanchan and Krishan, 2018).
Month Expenses x- mean (x-
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
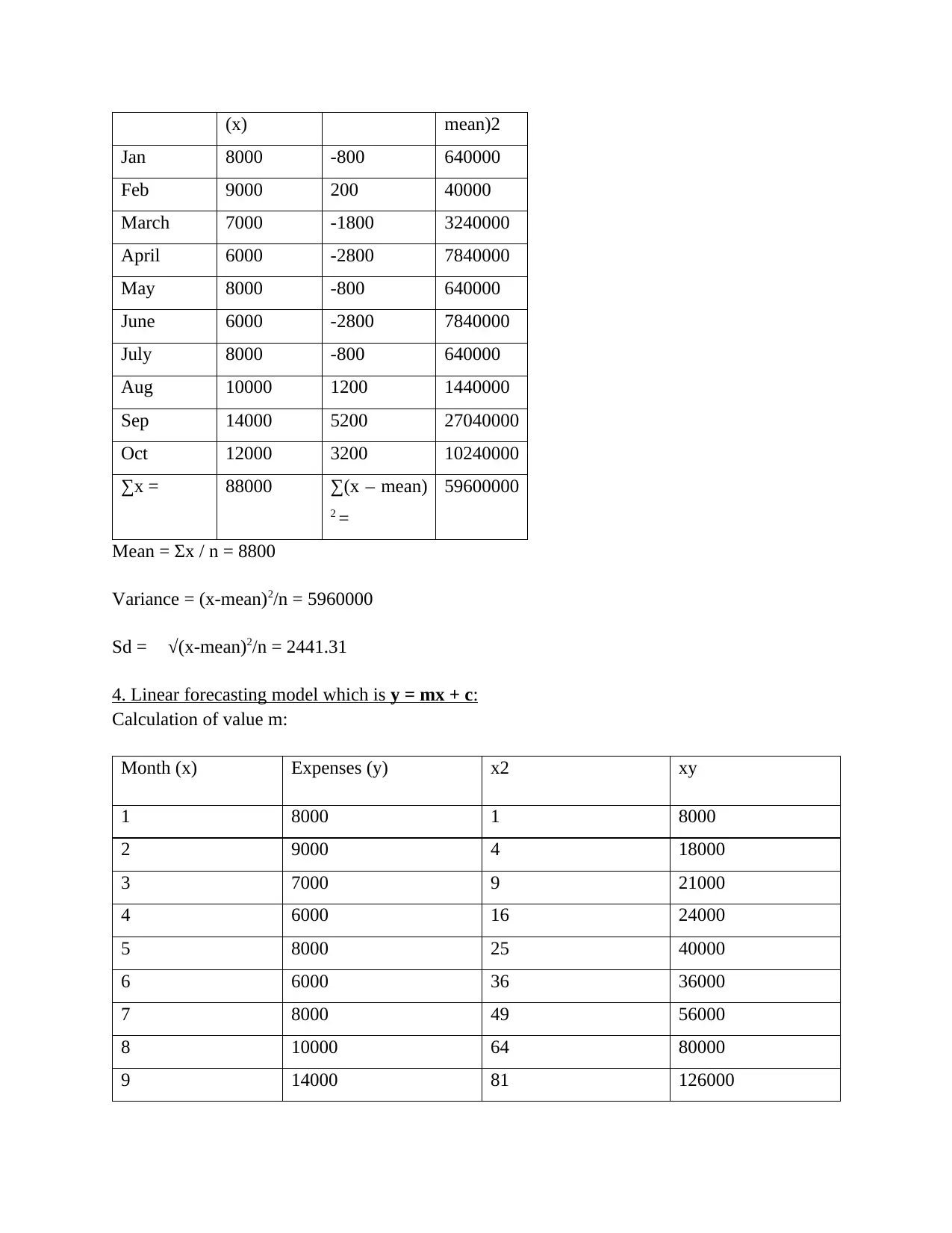
(x) mean)2
Jan 8000 -800 640000
Feb 9000 200 40000
March 7000 -1800 3240000
April 6000 -2800 7840000
May 8000 -800 640000
June 6000 -2800 7840000
July 8000 -800 640000
Aug 10000 1200 1440000
Sep 14000 5200 27040000
Oct 12000 3200 10240000
∑x = 88000 ∑(x – mean)
2 =
59600000
Mean = Σx / n = 8800
Variance = (x-mean)2/n = 5960000
Sd = √(x-mean)2/n = 2441.31
4. Linear forecasting model which is y = mx + c:
Calculation of value m:
Month (x) Expenses (y) x2 xy
1 8000 1 8000
2 9000 4 18000
3 7000 9 21000
4 6000 16 24000
5 8000 25 40000
6 6000 36 36000
7 8000 49 56000
8 10000 64 80000
9 14000 81 126000
Jan 8000 -800 640000
Feb 9000 200 40000
March 7000 -1800 3240000
April 6000 -2800 7840000
May 8000 -800 640000
June 6000 -2800 7840000
July 8000 -800 640000
Aug 10000 1200 1440000
Sep 14000 5200 27040000
Oct 12000 3200 10240000
∑x = 88000 ∑(x – mean)
2 =
59600000
Mean = Σx / n = 8800
Variance = (x-mean)2/n = 5960000
Sd = √(x-mean)2/n = 2441.31
4. Linear forecasting model which is y = mx + c:
Calculation of value m:
Month (x) Expenses (y) x2 xy
1 8000 1 8000
2 9000 4 18000
3 7000 9 21000
4 6000 16 24000
5 8000 25 40000
6 6000 36 36000
7 8000 49 56000
8 10000 64 80000
9 14000 81 126000

10 12000 100 120000
Σx = 55 Σy = 88000 Σx2 = 385 Σxy = 529000
y = mx + c
Here, m = n (∑xy) - (∑x) (∑y)/ n(∑x2)-( ∑x)2
= 10*(529000)-(55)*(88000)/10*(385)-(55) 2
= 5290000-4840000/3850-3025
= 450000/825
= 545.4545455
Calculation of c:
c = [(∑y) / n]-m (∑x/n)
= [88000/10]- 545.4545 (55/10)
= 8800-3000
= 5800
Forecasting for 11 and 15 days:
Forecasting for day 11:
y = mx + c
= 545.45 x 11 + 5800
= 11799.9995 or 11800
Forecasting for day 15:
= 545.4545 * 15 + 5800
= 13981.82 or around 14000
Σx = 55 Σy = 88000 Σx2 = 385 Σxy = 529000
y = mx + c
Here, m = n (∑xy) - (∑x) (∑y)/ n(∑x2)-( ∑x)2
= 10*(529000)-(55)*(88000)/10*(385)-(55) 2
= 5290000-4840000/3850-3025
= 450000/825
= 545.4545455
Calculation of c:
c = [(∑y) / n]-m (∑x/n)
= [88000/10]- 545.4545 (55/10)
= 8800-3000
= 5800
Forecasting for 11 and 15 days:
Forecasting for day 11:
y = mx + c
= 545.45 x 11 + 5800
= 11799.9995 or 11800
Forecasting for day 15:
= 545.4545 * 15 + 5800
= 13981.82 or around 14000

CONCLUSION
Form above study this has been asserted that Data analysis is defined as procedure of
analyzing, converting and modelling of data to presents useful information for business decision
making. The main aim of this analysis to extract useful information from data and take right
decision in regard of future activities. For this analysis require to use different types of
techniques that helps to forecast future trends effectively.
Form above study this has been asserted that Data analysis is defined as procedure of
analyzing, converting and modelling of data to presents useful information for business decision
making. The main aim of this analysis to extract useful information from data and take right
decision in regard of future activities. For this analysis require to use different types of
techniques that helps to forecast future trends effectively.
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

REFERENCES
Books and journal:
Kamilaris, A., Kartakoullis, A. and Prenafeta-Boldú, F.X., 2017. A review on the practice of big
data analysis in agriculture. Computers and Electronics in Agriculture, 143, pp.23-37.
Amrhein, V., Trafimow, D. and Greenland, S., 2019. Inferential statistics as descriptive statistics:
There is no replication crisis if we don’t expect replication. The American
Statistician, 73(sup1), pp.262-270.
Andrews, I., Gentzkow, M. and Shapiro, J.M., 2020. On the informativeness of descriptive
statistics for structural estimates. Econometrica, 88(6), pp.2231-2258.
Sharma, S.K., Kanchan, T. and Krishan, K., 2018. Descriptive statistics. The Encyclopedia of
Archaeological Sciences, pp.1-8.
Books and journal:
Kamilaris, A., Kartakoullis, A. and Prenafeta-Boldú, F.X., 2017. A review on the practice of big
data analysis in agriculture. Computers and Electronics in Agriculture, 143, pp.23-37.
Amrhein, V., Trafimow, D. and Greenland, S., 2019. Inferential statistics as descriptive statistics:
There is no replication crisis if we don’t expect replication. The American
Statistician, 73(sup1), pp.262-270.
Andrews, I., Gentzkow, M. and Shapiro, J.M., 2020. On the informativeness of descriptive
statistics for structural estimates. Econometrica, 88(6), pp.2231-2258.
Sharma, S.K., Kanchan, T. and Krishan, K., 2018. Descriptive statistics. The Encyclopedia of
Archaeological Sciences, pp.1-8.
1 out of 11
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.





