Numeracy and Data Analysis

This document discusses various topics related to numeracy and data analysis. It covers arranging data in tables, presenting data using charts, calculation steps for mean, median, mode, range, and standard deviation, and using linear forecasting models. The document provides examples and analysis for each topic.

NUMERACY AND DATA
ANALYSIS

TABLE OF CONTENTS
TABLE OF CONTENTS................................................................................................................2
TASK...............................................................................................................................................1
1. Arranging data in form of table...............................................................................................1
2. Presentation of the data using 2 types of the charts.................................................................1
3. Steps for the calculation and highlighting financial issues......................................................2
4. Using the linear forecasting models that is y = mx +c............................................................5
REFERENCES................................................................................................................................7

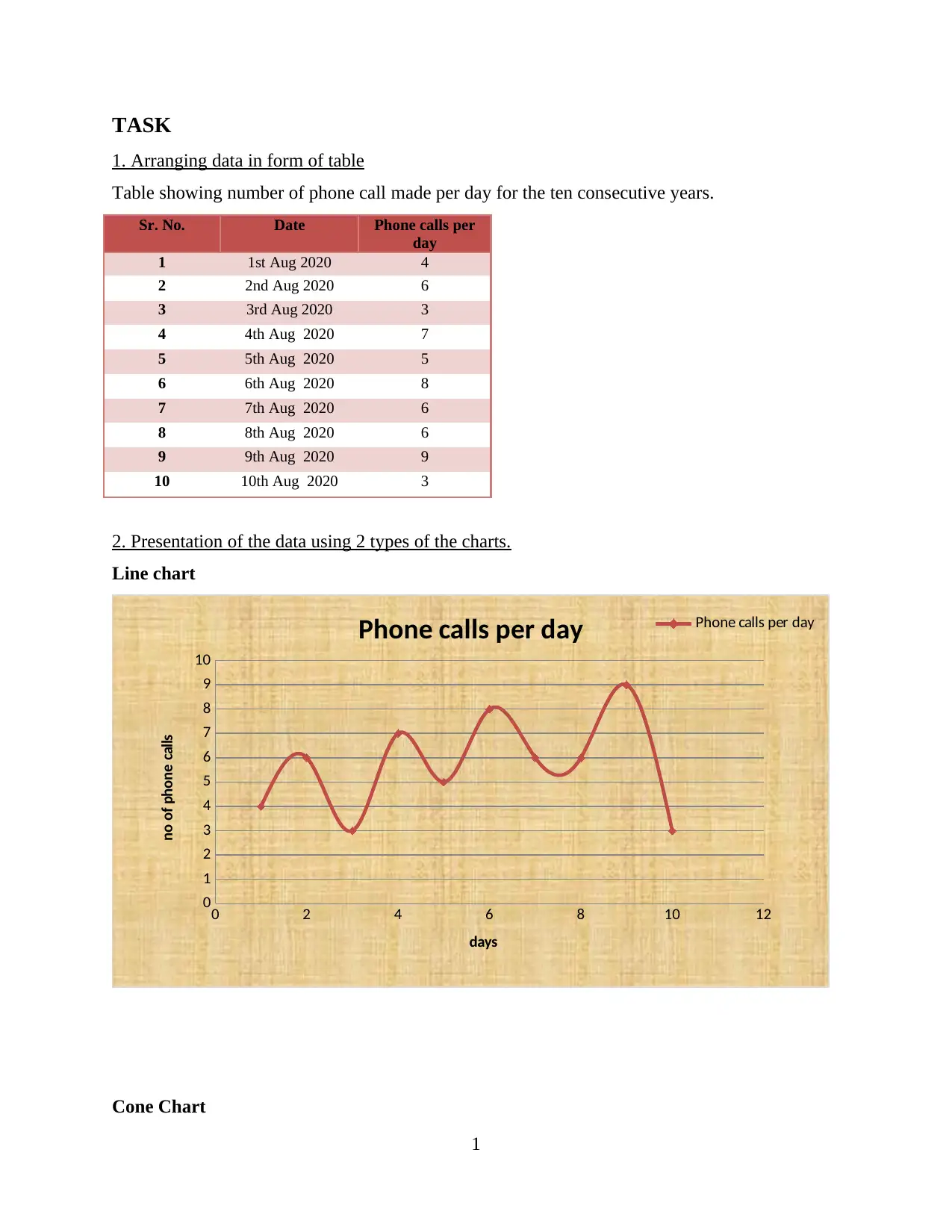
TASK
1. Arranging data in form of table
Table showing number of phone call made per day for the ten consecutive years.
Sr. No. Date Phone calls per
day
1 1st Aug 2020 4
2 2nd Aug 2020 6
3 3rd Aug 2020 3
4 4th Aug 2020 7
5 5th Aug 2020 5
6 6th Aug 2020 8
7 7th Aug 2020 6
8 8th Aug 2020 6
9 9th Aug 2020 9
10 10th Aug 2020 3
2. Presentation of the data using 2 types of the charts.
Line chart
0 2 4 6 8 10 12
0
1
2
3
4
5
6
7
8
9
10
Phone calls per day Phone calls per day
days
no of phone calls
Cone Chart
1

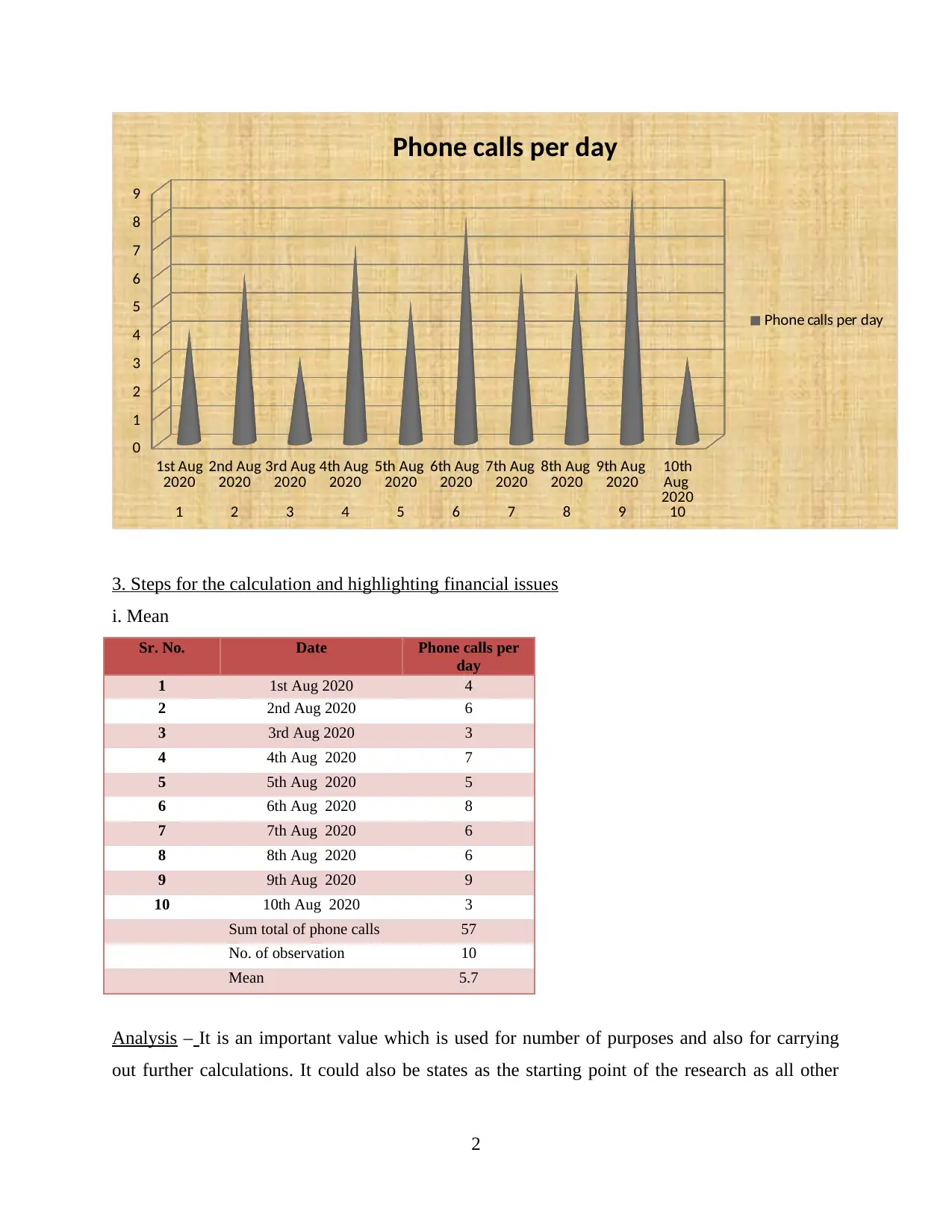
1st Aug
2020 2nd Aug
2020 3rd Aug
2020 4th Aug
2020 5th Aug
2020 6th Aug
2020 7th Aug
2020 8th Aug
2020 9th Aug
2020 10th
Aug
2020
1 2 3 4 5 6 7 8 9 10
0
1
2
3
4
5
6
7
8
9
Phone calls per day
Phone calls per day
3. Steps for the calculation and highlighting financial issues
i. Mean
Sr. No. Date Phone calls per
day
1 1st Aug 2020 4
2 2nd Aug 2020 6
3 3rd Aug 2020 3
4 4th Aug 2020 7
5 5th Aug 2020 5
6 6th Aug 2020 8
7 7th Aug 2020 6
8 8th Aug 2020 6
9 9th Aug 2020 9
10 10th Aug 2020 3
Sum total of phone calls 57
No. of observation 10
Mean 5.7
Analysis – It is an important value which is used for number of purposes and also for carrying
out further calculations. It could also be states as the starting point of the research as all other
2

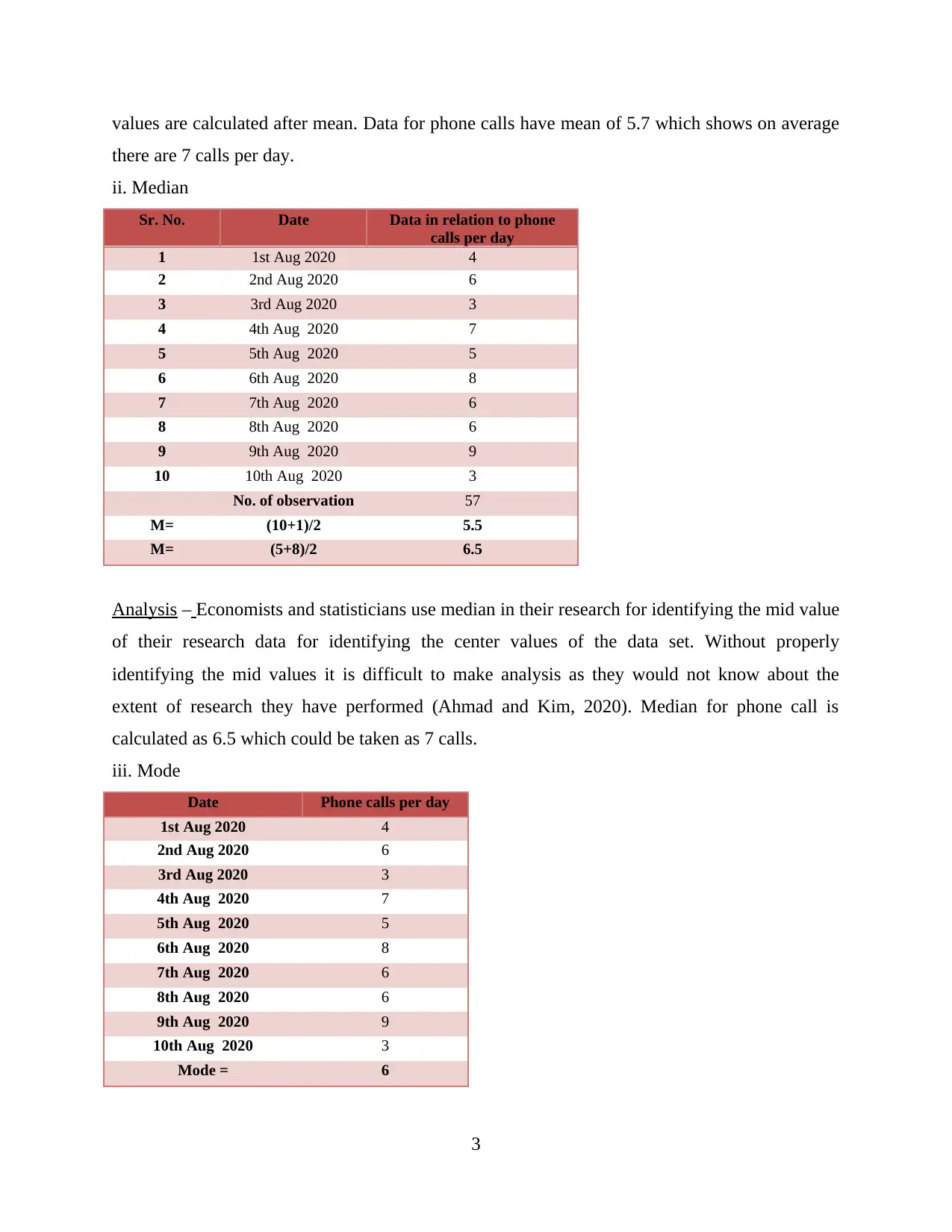
values are calculated after mean. Data for phone calls have mean of 5.7 which shows on average
there are 7 calls per day.
ii. Median
Sr. No. Date Data in relation to phone
calls per day
1 1st Aug 2020 4
2 2nd Aug 2020 6
3 3rd Aug 2020 3
4 4th Aug 2020 7
5 5th Aug 2020 5
6 6th Aug 2020 8
7 7th Aug 2020 6
8 8th Aug 2020 6
9 9th Aug 2020 9
10 10th Aug 2020 3
No. of observation 57
M= (10+1)/2 5.5
M= (5+8)/2 6.5
Analysis – Economists and statisticians use median in their research for identifying the mid value
of their research data for identifying the center values of the data set. Without properly
identifying the mid values it is difficult to make analysis as they would not know about the
extent of research they have performed (Ahmad and Kim, 2020). Median for phone call is
calculated as 6.5 which could be taken as 7 calls.
iii. Mode
Date Phone calls per day
1st Aug 2020 4
2nd Aug 2020 6
3rd Aug 2020 3
4th Aug 2020 7
5th Aug 2020 5
6th Aug 2020 8
7th Aug 2020 6
8th Aug 2020 6
9th Aug 2020 9
10th Aug 2020 3
Mode = 6
3

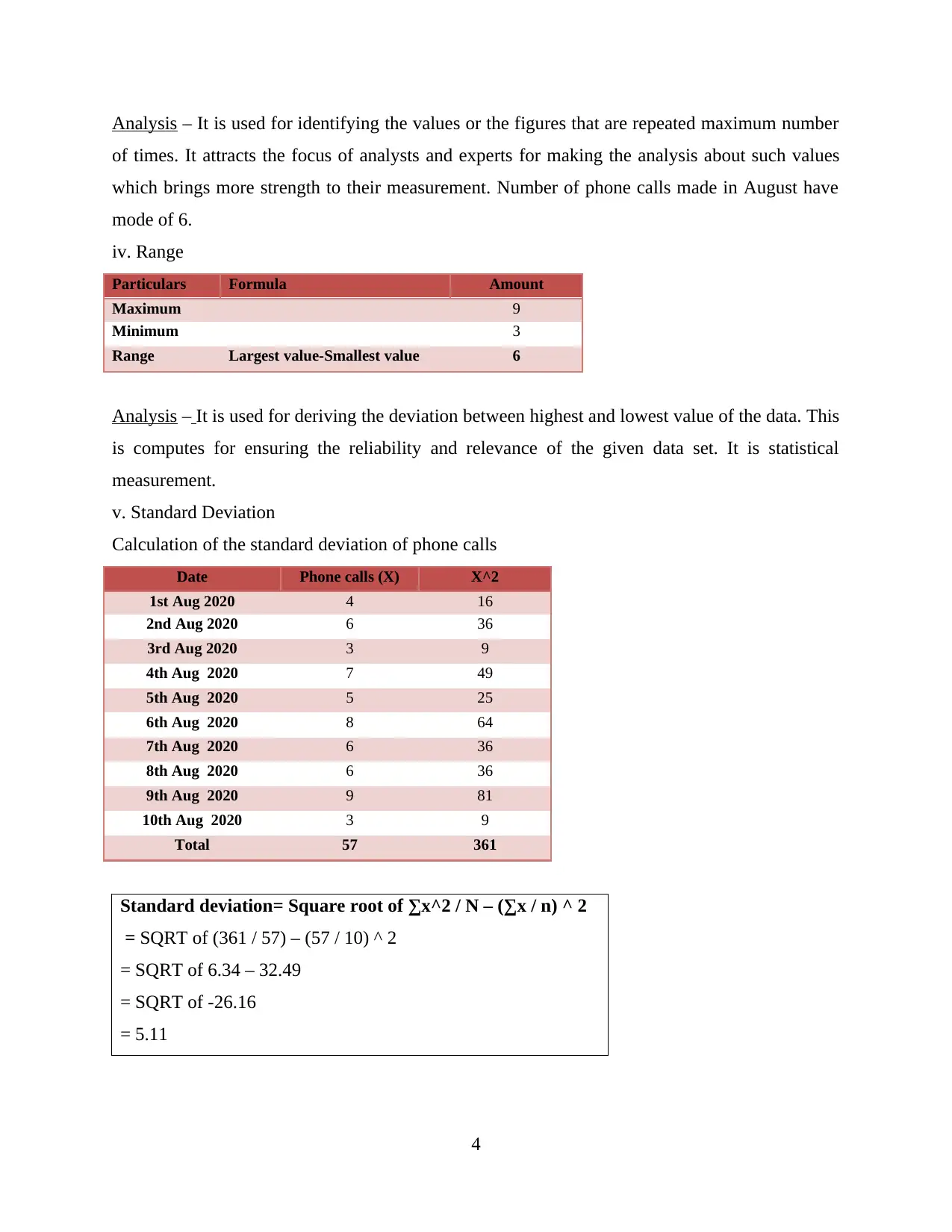
Analysis – It is used for identifying the values or the figures that are repeated maximum number
of times. It attracts the focus of analysts and experts for making the analysis about such values
which brings more strength to their measurement. Number of phone calls made in August have
mode of 6.
iv. Range
Particulars Formula Amount
Maximum 9
Minimum 3
Range Largest value-Smallest value 6
Analysis – It is used for deriving the deviation between highest and lowest value of the data. This
is computes for ensuring the reliability and relevance of the given data set. It is statistical
measurement.
v. Standard Deviation
Calculation of the standard deviation of phone calls
Date Phone calls (X) X^2
1st Aug 2020 4 16
2nd Aug 2020 6 36
3rd Aug 2020 3 9
4th Aug 2020 7 49
5th Aug 2020 5 25
6th Aug 2020 8 64
7th Aug 2020 6 36
8th Aug 2020 6 36
9th Aug 2020 9 81
10th Aug 2020 3 9
Total 57 361
Standard deviation= Square root of ∑x^2 / N – (∑x / n) ^ 2
= SQRT of (361 / 57) – (57 / 10) ^ 2
= SQRT of 6.34 – 32.49
= SQRT of -26.16
= 5.11
4

Analysis – The calculation of the standard deviation is done by the analysts and experts for
identifying the variation of the results from its mean values (Reyes-Urueña and et.al., 2018).
Standard deviation of the given data for phone calls is 5.11. The deviation is not high from the
mean value.
4. Using the linear forecasting models that is y = mx +c
Computation of the values used in linear forecasting
Date X Phone calls (Y) X*Y X^2
1st Aug 2020 1 4 4 1
2nd Aug 2020 2 6 12 4
3rd Aug 2020 3 3 9 9
4th Aug 2020 4 7 28 16
5th Aug 2020 5 5 25 25
6th Aug 2020 6 8 48 36
7th Aug 2020 7 6 42 49
8th Aug 2020 8 6 48 64
9th Aug 2020 9 9 81 81
10th Aug 2020 10 3 30 100
Total 55 57 327 385
i) steps showing calculation of the m value
m = NΣxy – Σx Σy / NΣ x^2 – (Σx)^2
Y = mX + c
m = 10 (327) - (55 * 57) / (10 * 385) – (55)^2
m = (3870 – 3135) / (3850 – 3025)
m = 735 / 825
m = 0.89
ii) steps showing calculation of the c value
c = Σy – m Σx / N
c = 57 – (0.89 * 55) / 10
c = (57 – 49) / 10
c = 8 / 10
c = 0.8
iii) Forecasting number of calls made on 12th and 14th day using m and c values.
For 12th day -
5

Y = mX + c
= 0.89 * (12) + (0.8)
= 10.68 + 0.8
= 11.48 = 11 approx
For 14th day -
Y = mX + c
= 0.89 * (14) + (0.8)
= 12.46 + 0.8
= 13.26 = 13 approx
Analysis – The above computation shows that the method is highly useful in making forecasts
about the future values based on the previous business trends (Mohd Saifudin, Othman and
Mohamed Elias, 2017). The phone calls are estimated to be 11 on 12th day of August and 13 calls
on 14th day of August. This shows growing trend of the phone calls.
6

REFERENCES
Books and Journals
Mohd Saifudin, A., Othman, S.N. and Mohamed Elias, E., 2017. Critical factors of the new
Islamic supply chain model through the lens of descriptive data analysis. International
Journal of Supply Chain Management (IJSCM). 6(1). pp.203-208.
Reyes-Urueña, J.M., and et.al., 2018. Estimating the HIV undiagnosed population in Catalonia,
Spain: descriptive and comparative data analysis to identify differences in MSM stratified
by migrant and Spanish-born population. BMJ open. 8(2).
Ahmad, S. and Kim, D.H., 2020. Quantum GIS based descriptive and predictive data analysis for
effective planning of waste management. IEEE Access. 8. pp.46193-46205.
7