Numeracy and Data Analysis
VerifiedAdded on 2023/01/07
|10
|1645
|65
AI Summary
This document provides a comprehensive guide on numeracy and data analysis. It explains the importance of data analysis and its application in making informed decisions. The document covers topics such as arranging data into table format, presenting data using charts, computation of mean, median, mode, standard deviation, and the use of a linear forecasting model. It also includes a conclusion highlighting the significance of data analysis in daily decision-making.
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

Numeracy and Data
Analysis
Analysis
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

Contents
INTRODUCTION...........................................................................................................................................3
MAIN BODY.................................................................................................................................................3
1. Arranging data into table format:.........................................................................................................3
2. Present above data using charts:..........................................................................................................4
3. Computation and highlight final value.................................................................................................5
4. Use of linear forecasting model i.e. y = mx + c to compute and make discussion on followings:.......7
CONCLUSION...............................................................................................................................................9
REFERENCES..............................................................................................................................................10
INTRODUCTION...........................................................................................................................................3
MAIN BODY.................................................................................................................................................3
1. Arranging data into table format:.........................................................................................................3
2. Present above data using charts:..........................................................................................................4
3. Computation and highlight final value.................................................................................................5
4. Use of linear forecasting model i.e. y = mx + c to compute and make discussion on followings:.......7
CONCLUSION...............................................................................................................................................9
REFERENCES..............................................................................................................................................10
INTRODUCTION
Numeracy is understanding, knowledge, attitudes and criteria that are needed in a diverse
variety of possible outcome and scenarios in mathematical. Whereas the phrase data-analysis is
defined as data review, preparation, and improvement and provide accurate, useful
intelligence.Numeracy includes skills not often learned in the course, the capacity to use figures
and to address real-life problems. It includes being willing to use calculations and quantitative
methods in all areas of life with faith and ability(Del Río and et.al, 2017). Numeracy is of equal
value to education.Data Analysis is the method by which quantitative and/or logical methods are
regularly applied to explain and demonstrate, compress and recapture and analyze data.
Authentic and precise review of the study results is an important way of ensuring data security.
This report consists of phone calls making per day and make two types of charts. Along with
calculate mean, median, mode, standard deviation and linear forecasting model.
MAIN BODY
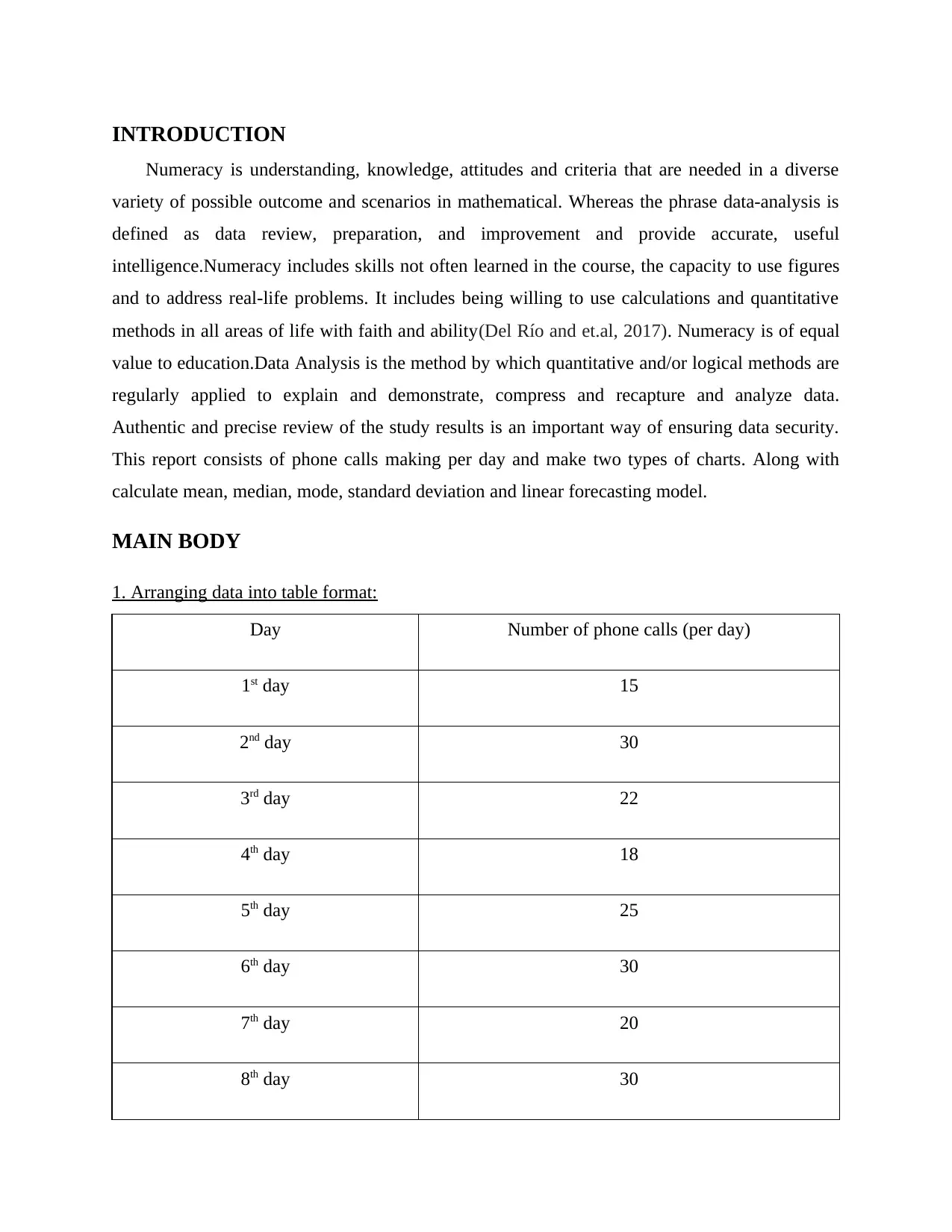
1. Arranging data into table format:
Day Number of phone calls (per day)
1st day 15
2nd day 30
3rd day 22
4th day 18
5th day 25
6th day 30
7th day 20
8th day 30
Numeracy is understanding, knowledge, attitudes and criteria that are needed in a diverse
variety of possible outcome and scenarios in mathematical. Whereas the phrase data-analysis is
defined as data review, preparation, and improvement and provide accurate, useful
intelligence.Numeracy includes skills not often learned in the course, the capacity to use figures
and to address real-life problems. It includes being willing to use calculations and quantitative
methods in all areas of life with faith and ability(Del Río and et.al, 2017). Numeracy is of equal
value to education.Data Analysis is the method by which quantitative and/or logical methods are
regularly applied to explain and demonstrate, compress and recapture and analyze data.
Authentic and precise review of the study results is an important way of ensuring data security.
This report consists of phone calls making per day and make two types of charts. Along with
calculate mean, median, mode, standard deviation and linear forecasting model.
MAIN BODY
1. Arranging data into table format:
Day Number of phone calls (per day)
1st day 15
2nd day 30
3rd day 22
4th day 18
5th day 25
6th day 30
7th day 20
8th day 30

9th day 15
10th day 28
2. Present above data using charts:
Column chart:The Column Chart comparisons a specific collection of data pointed successfully
but it highlights while contrasting several sets. Note that averages are not included in the data
sequence. Since by each series data Excel requires a different color, it is simple to see that a
particular pattern evolves over time, or to contrast several sets throughout a given period of time.
The Grouped Chart of Columns is particularly common(Lore, Wang and Buckley, 2016).
1st
day 2nd
day 3rd
day 4th
day 5th
day 6th
day 7th
day 8th
day 9th
day 10th
day
0
5
10
15
20
25
30
15
30
22
18
25
30
20
30
15
28
Number of phone calls (per day)
Number of phone calls
(per day)
Line chart:The Line Chart is particularly useful in showing patterns. The vertical line (Y-axis)
often shows numerical values, while the horizontal line (X-axis) indicates time or other groups.
The Line Chart is similarly useful in showing numerous-series patterns as seen through markers
in the above line chart. Note that each line reflects a contrasting shade. While not as colorful as
the other maps, the usefulness of the line chart in displaying a pattern for a single episode and
contrasting patterns for different sequence of data points is easy to see.
10th day 28
2. Present above data using charts:
Column chart:The Column Chart comparisons a specific collection of data pointed successfully
but it highlights while contrasting several sets. Note that averages are not included in the data
sequence. Since by each series data Excel requires a different color, it is simple to see that a
particular pattern evolves over time, or to contrast several sets throughout a given period of time.
The Grouped Chart of Columns is particularly common(Lore, Wang and Buckley, 2016).
1st
day 2nd
day 3rd
day 4th
day 5th
day 6th
day 7th
day 8th
day 9th
day 10th
day
0
5
10
15
20
25
30
15
30
22
18
25
30
20
30
15
28
Number of phone calls (per day)
Number of phone calls
(per day)
Line chart:The Line Chart is particularly useful in showing patterns. The vertical line (Y-axis)
often shows numerical values, while the horizontal line (X-axis) indicates time or other groups.
The Line Chart is similarly useful in showing numerous-series patterns as seen through markers
in the above line chart. Note that each line reflects a contrasting shade. While not as colorful as
the other maps, the usefulness of the line chart in displaying a pattern for a single episode and
contrasting patterns for different sequence of data points is easy to see.
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

1st
day 2nd
day 3rd
day 4th
day 5th
day 6th
day 7th
day 8th
day 9th
day 10th
day
0
5
10
15
20
25
30
35
15
30
22
18
25
30
20
30
15
28
Number of phone calls (per day)
Number of phone calls
(per day)
3. Computation and highlight final value
Mean:The "Mean" is done by multiplying all the digits in the information combined and
separated by the number elements in the database.
Day Number of phone calls (per day)
1st day 15
2nd day 30
3rd day 22
4th day 18
5th day 25
6th day 30
7th day 20
8th day 30
9th day 15
10th day 28
∑x = Sum of all the phone
calls 233
Mean = ∑x / n = 233 / 10 = 23.3
day 2nd
day 3rd
day 4th
day 5th
day 6th
day 7th
day 8th
day 9th
day 10th
day
0
5
10
15
20
25
30
35
15
30
22
18
25
30
20
30
15
28
Number of phone calls (per day)
Number of phone calls
(per day)
3. Computation and highlight final value
Mean:The "Mean" is done by multiplying all the digits in the information combined and
separated by the number elements in the database.
Day Number of phone calls (per day)
1st day 15
2nd day 30
3rd day 22
4th day 18
5th day 25
6th day 30
7th day 20
8th day 30
9th day 15
10th day 28
∑x = Sum of all the phone
calls 233
Mean = ∑x / n = 233 / 10 = 23.3

Interpretation: As per the above table put all the consecutive calls that conduct by a person and
get the amount of 233 sum of 10 days after that dvide by the 10 days and get amount of mean
23.3Median: Median is the value that represents the central ground since all the measurements
are grouped in an upward / downward order. The center frequency is split into precisely two
parts. Fifty per cent of an allocation's results have ratings on below the average. So the median is
the fiftieth percent(Taylor and Byrne-Davis, 2016).
As here, selected data is of even number i.e. 10 days. Thus Median would be = [(10/2) + (10/2
+1) value] / 2 = (5th value + 6th value )/2 = (25 + 30)/2 = 27.5
From the table set select the 5th and 6th amount that calculates as per the equation and get
the amount of 27.5
Mode: Mode is defined as the most commonly seen value in the results. Some sets of data do not
even have a mode, since each meaning only happens once. Some data sets on the other hand may
have more than one mode. This occurs when two or more variables of similar frequency in the
sample group which would be larger than just about every other quality. This method reflects on
the biggest value in data range which is 30.
Range:For a data set, the "Range" is the variance between the greatest value and lowest value in
the sample group. Rearrange the statistical model first from then deduct the first component
since the last component, lowest to the highest.
Maximum Range = Highest Value i.e. 30
Minimum Range = Smallest Value i.e. 15
To calculate the range select highest value from the table which is 30 and select lowest
value which is 15
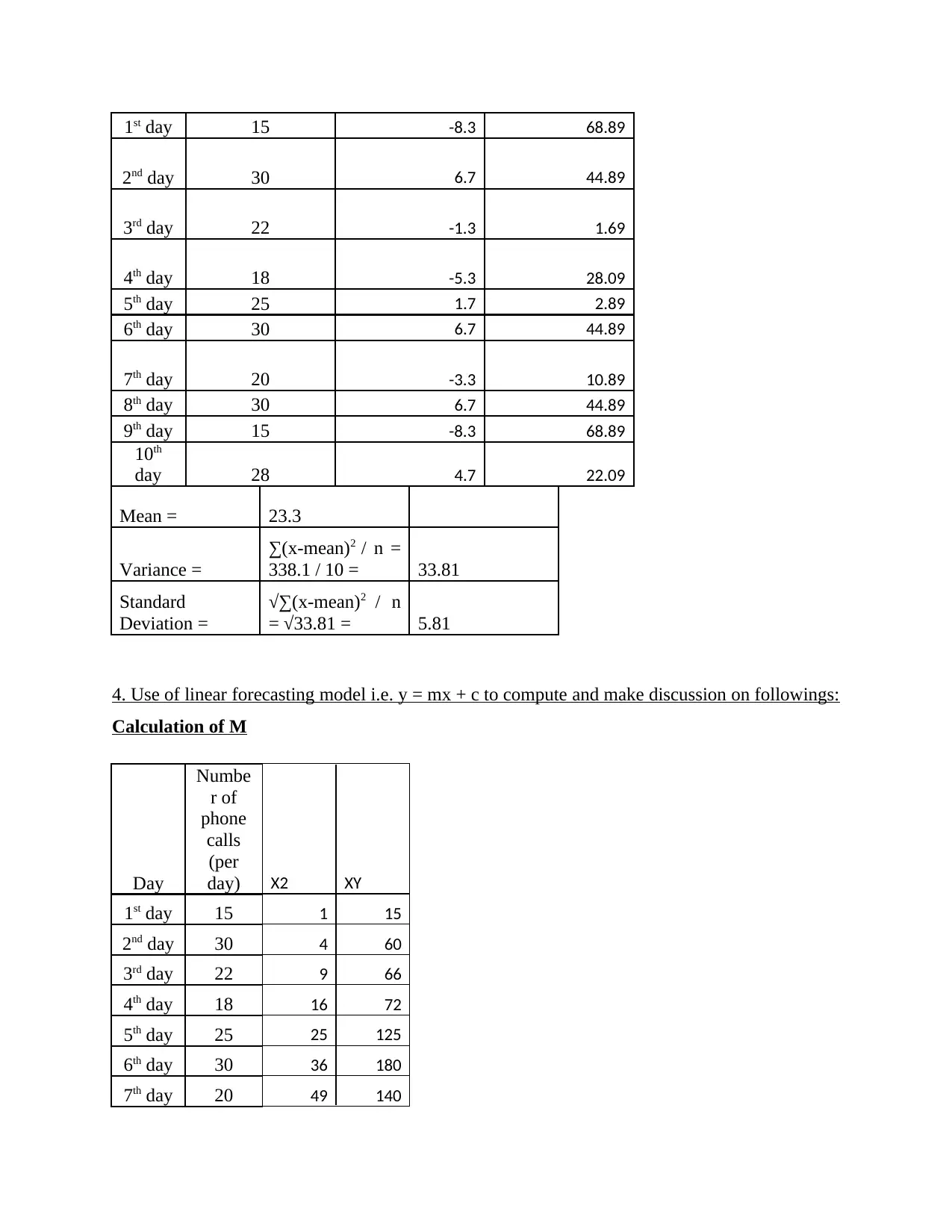
Standard deviation: The standard deviation is a calculation of the points distributed across a
sample group. In general, they are concerned in a population's standard deviation. Even so, as
information from a survey is often provided instead, they can approximate the standard deviation
of the community from a standard deviation of the measurements (Zippert and Rittle-Johnson,
2020).
Day
Number of phone
calls (per day) X- mean (x-mean)2
get the amount of 233 sum of 10 days after that dvide by the 10 days and get amount of mean
23.3Median: Median is the value that represents the central ground since all the measurements
are grouped in an upward / downward order. The center frequency is split into precisely two
parts. Fifty per cent of an allocation's results have ratings on below the average. So the median is
the fiftieth percent(Taylor and Byrne-Davis, 2016).
As here, selected data is of even number i.e. 10 days. Thus Median would be = [(10/2) + (10/2
+1) value] / 2 = (5th value + 6th value )/2 = (25 + 30)/2 = 27.5
From the table set select the 5th and 6th amount that calculates as per the equation and get
the amount of 27.5
Mode: Mode is defined as the most commonly seen value in the results. Some sets of data do not
even have a mode, since each meaning only happens once. Some data sets on the other hand may
have more than one mode. This occurs when two or more variables of similar frequency in the
sample group which would be larger than just about every other quality. This method reflects on
the biggest value in data range which is 30.
Range:For a data set, the "Range" is the variance between the greatest value and lowest value in
the sample group. Rearrange the statistical model first from then deduct the first component
since the last component, lowest to the highest.
Maximum Range = Highest Value i.e. 30
Minimum Range = Smallest Value i.e. 15
To calculate the range select highest value from the table which is 30 and select lowest
value which is 15
Standard deviation: The standard deviation is a calculation of the points distributed across a
sample group. In general, they are concerned in a population's standard deviation. Even so, as
information from a survey is often provided instead, they can approximate the standard deviation
of the community from a standard deviation of the measurements (Zippert and Rittle-Johnson,
2020).
Day
Number of phone
calls (per day) X- mean (x-mean)2
1st day 15 -8.3 68.89
2nd day 30 6.7 44.89
3rd day 22 -1.3 1.69
4th day 18 -5.3 28.09
5th day 25 1.7 2.89
6th day 30 6.7 44.89
7th day 20 -3.3 10.89
8th day 30 6.7 44.89
9th day 15 -8.3 68.89
10th
day 28 4.7 22.09
Mean = 23.3
Variance =
∑(x-mean)2 / n =
338.1 / 10 = 33.81
Standard
Deviation =
√∑(x-mean)2 / n
= √33.81 = 5.81
4. Use of linear forecasting model i.e. y = mx + c to compute and make discussion on followings:
Calculation of M
Day
Numbe
r of
phone
calls
(per
day) X2 XY
1st day 15 1 15
2nd day 30 4 60
3rd day 22 9 66
4th day 18 16 72
5th day 25 25 125
6th day 30 36 180
7th day 20 49 140
2nd day 30 6.7 44.89
3rd day 22 -1.3 1.69
4th day 18 -5.3 28.09
5th day 25 1.7 2.89
6th day 30 6.7 44.89
7th day 20 -3.3 10.89
8th day 30 6.7 44.89
9th day 15 -8.3 68.89
10th
day 28 4.7 22.09
Mean = 23.3
Variance =
∑(x-mean)2 / n =
338.1 / 10 = 33.81
Standard
Deviation =
√∑(x-mean)2 / n
= √33.81 = 5.81
4. Use of linear forecasting model i.e. y = mx + c to compute and make discussion on followings:
Calculation of M
Day
Numbe
r of
phone
calls
(per
day) X2 XY
1st day 15 1 15
2nd day 30 4 60
3rd day 22 9 66
4th day 18 16 72
5th day 25 25 125
6th day 30 36 180
7th day 20 49 140
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

8th day 30 64 240
9th day 15 81 135
10th
day 28 100 280
X = 55 233
X2 =
385 1313
m = N∑xy- ∑x∑y / N∑ X2 - (∑x)2
= 10*1313 – 55*233 / 10*385 – (55)2
= 13130 – 12815/ 3850 – 3025
= 315 / 825
= 0.38
Calculation of C
c = [(∑y / n)-m (∑x/n)]
= [(233 /10) - (0.38) (55/10)]
= 23.3 + 2.09
= 25.39
Forecasting of number of calls
At 12th day:
Y = m x+ c
= 0.38 *12 + 25.39
= 4.56 + 25.39
= 29.95 or around 30 calls on 12th day
9th day 15 81 135
10th
day 28 100 280
X = 55 233
X2 =
385 1313
m = N∑xy- ∑x∑y / N∑ X2 - (∑x)2
= 10*1313 – 55*233 / 10*385 – (55)2
= 13130 – 12815/ 3850 – 3025
= 315 / 825
= 0.38
Calculation of C
c = [(∑y / n)-m (∑x/n)]
= [(233 /10) - (0.38) (55/10)]
= 23.3 + 2.09
= 25.39
Forecasting of number of calls
At 12th day:
Y = m x+ c
= 0.38 *12 + 25.39
= 4.56 + 25.39
= 29.95 or around 30 calls on 12th day

At 14th day:
Y = m x+ c
= 0.38 *14 + 25.39
= 5.32 + 25.39
= 30.71 or around 31 calls on 14thday.
CONCLUSION
As per the above discussion it has been concluded that data-analysis is very necessary to
eliminate relevant information from the existing image. It also assists the researcher by providing
different techniques to make wrong assumptions. It serves as the foundation for successful daily
decision making.
Y = m x+ c
= 0.38 *14 + 25.39
= 5.32 + 25.39
= 30.71 or around 31 calls on 14thday.
CONCLUSION
As per the above discussion it has been concluded that data-analysis is very necessary to
eliminate relevant information from the existing image. It also assists the researcher by providing
different techniques to make wrong assumptions. It serves as the foundation for successful daily
decision making.

REFERENCES
Books and Journal
Del Río, M. F. and et.al, 2017. Distinct influences of mothers and fathers on kindergartners’
numeracy performance: The role of math anxiety, home numeracy practices, and
numeracy expectations. Early Education and Development. 28(8). pp.939-955.
Lore, M.D., Wang, A.H. and Buckley, M.T., 2016. Effectiveness of a parent-child home
numeracy intervention on urban Catholic school first grade students. Journal of Catholic
Education. 19(3). pp.142-165.
Taylor, A.A. and Byrne-Davis, L.M., 2016. Clinician Numeracy: The Development of an
Assessment Measure for Doctors. Numeracy: Advancing Education in Quantitative
Literacy. 9(1).
Zippert, E.L. and Rittle-Johnson, B., 2020. The home math environment: More than
numeracy. Early Childhood Research Quarterly. 50. pp.4-15.
Books and Journal
Del Río, M. F. and et.al, 2017. Distinct influences of mothers and fathers on kindergartners’
numeracy performance: The role of math anxiety, home numeracy practices, and
numeracy expectations. Early Education and Development. 28(8). pp.939-955.
Lore, M.D., Wang, A.H. and Buckley, M.T., 2016. Effectiveness of a parent-child home
numeracy intervention on urban Catholic school first grade students. Journal of Catholic
Education. 19(3). pp.142-165.
Taylor, A.A. and Byrne-Davis, L.M., 2016. Clinician Numeracy: The Development of an
Assessment Measure for Doctors. Numeracy: Advancing Education in Quantitative
Literacy. 9(1).
Zippert, E.L. and Rittle-Johnson, B., 2020. The home math environment: More than
numeracy. Early Childhood Research Quarterly. 50. pp.4-15.
1 out of 10
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.





