Numeracy and Data Analysis

This document provides an introduction to numeracy and data analysis, covering topics such as data collection, arrangement, representation using charts, calculations of mean, median, mode, maximum, minimum, range, and linear forecasting models. It also includes a conclusion and references for further reading.

Numeracy and Data Analysis
1

INTRODUCTION...........................................................................................................................3
MAIN BODY..................................................................................................................................3
1. Arrangement of data................................................................................................................3
2. Using above arranged data represent two different charts.......................................................3
3. Calculate the following terms..................................................................................................5
4. Calculate y=mx+c by using linear forecasting model.............................................................7
CONCLUSION................................................................................................................................9
REFERENCES..............................................................................................................................10
2

INTRODUCTION
Data analysis is a method of data gathering and manipulation which enables everyone to
acquire useful knowledge (Friese, 2019). In other words, the study of data is primarily intended
to analyze what knowledge depends, whatever it needs, on interpretation. The study focuses
primarily on data collection in which data are linked to the payment of bills for several months.
The project report also includes a significant set of calculations such as mean, mode, medium
and predictions.
MAIN BODY
1. Arrangement of data
Months Type of bill Amount (in ‘00 pounds)
January Telephone bill 10
February Water bill 5
March Council taxation bill 20
April Rental charges or bill 17
May Bank statement 25
June Internet bill 20
July Transportation bill 9
August Grocery bill 30
September Electricity bill 10
October Heating bill 10
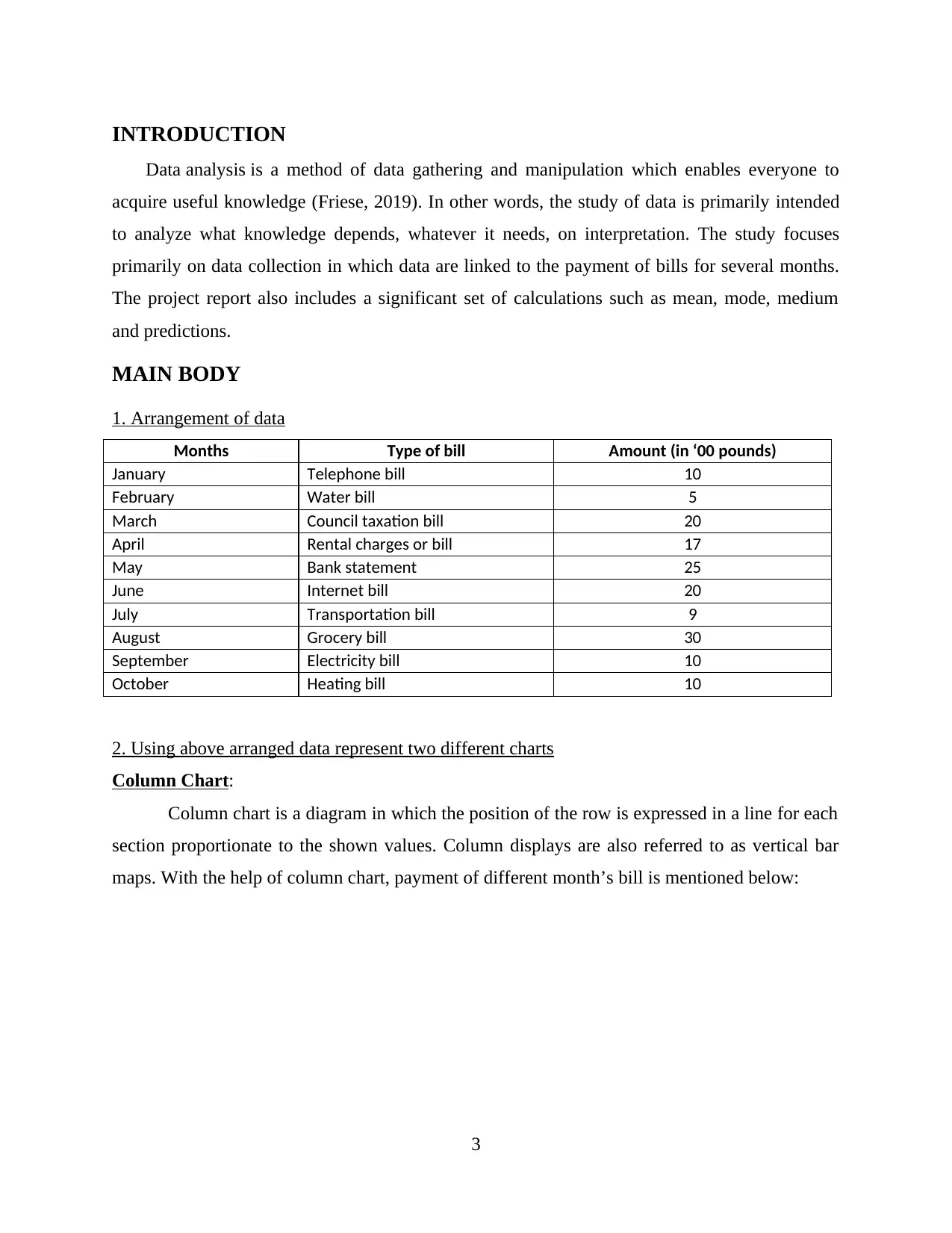
2. Using above arranged data represent two different charts
Column Chart:
Column chart is a diagram in which the position of the row is expressed in a line for each
section proportionate to the shown values. Column displays are also referred to as vertical bar
maps. With the help of column chart, payment of different month’s bill is mentioned below:
3

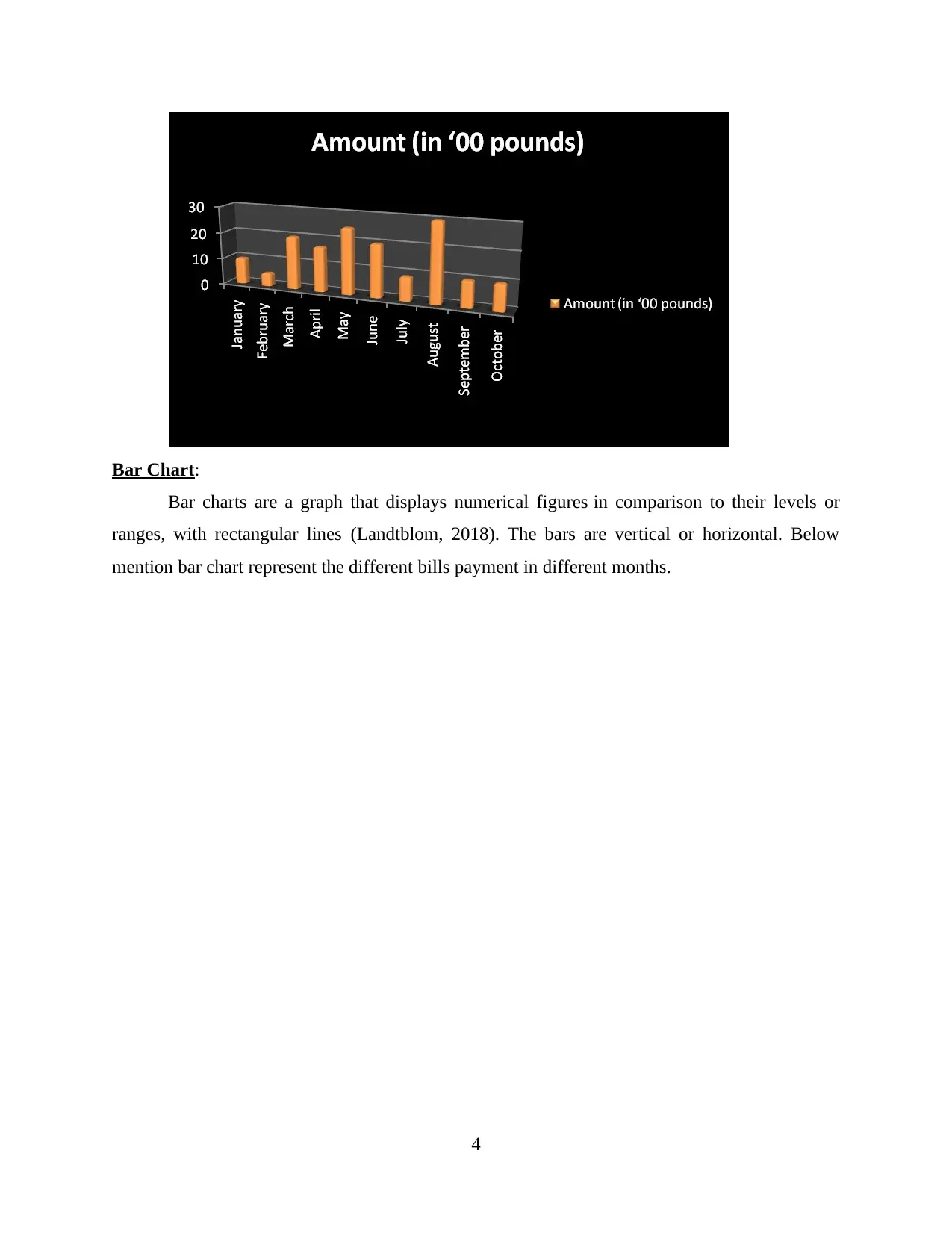
Bar Chart:
Bar charts are a graph that displays numerical figures in comparison to their levels or
ranges, with rectangular lines (Landtblom, 2018). The bars are vertical or horizontal. Below
mention bar chart represent the different bills payment in different months.
4

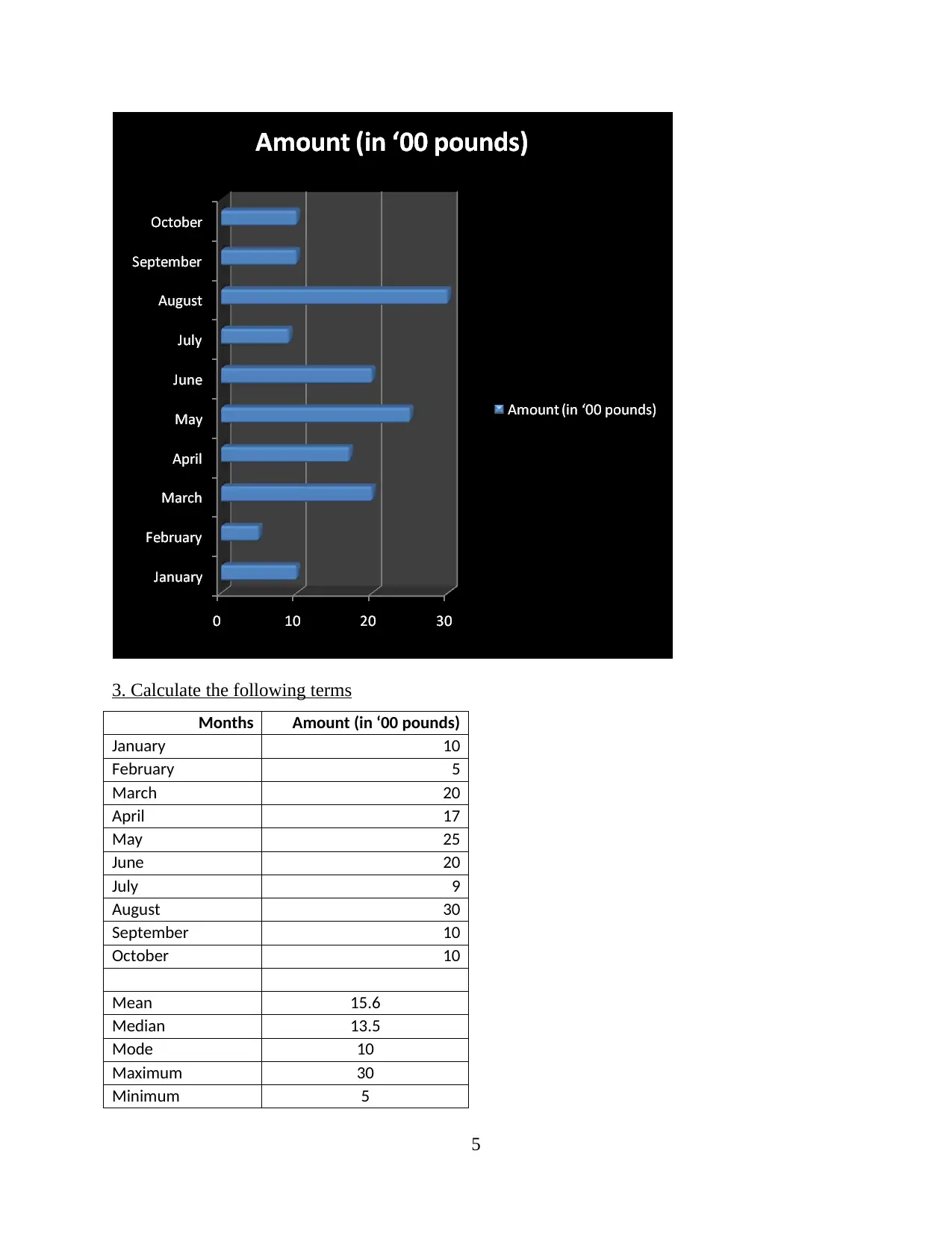
3. Calculate the following terms
Months Amount (in ‘00 pounds)
January 10
February 5
March 20
April 17
May 25
June 20
July 9
August 30
September 10
October 10
Mean 15.6
Median 13.5
Mode 10
Maximum 30
Minimum 5
5

Range 25
Mean: A quantitative sample of a single special variable is the most common term for an
average, which is the average number of any parameter (Sarkar and Rashid, 2016). Add and
break down the meanings of all terms in a variety of ways to determine this. The mean value is
measured below the following value of the bills.
Formula:
Mean= Sum of all observations /number of observations
= 156 /10
= 15.6
Median: In the sequence of numbers, the "median" is the middle value of the observation, if
there's no number and no element in the array. This is calculated using a formula:
Formula:
When data set is even= {N/2th item + N/2th item + 1}2
When data set is odd= (N+1) /2th item.
Months Amount (in ‘00 pounds)
January 5
February 9
March 10
April 10
May 10
June 17
July 20
August 20
September 25
October 30
Total observation is N= 10
M= (10/2th item + 10/2th item + 1)/2
= (5th item+ 6th item)/2
= 5.5th item
= 13.5
6

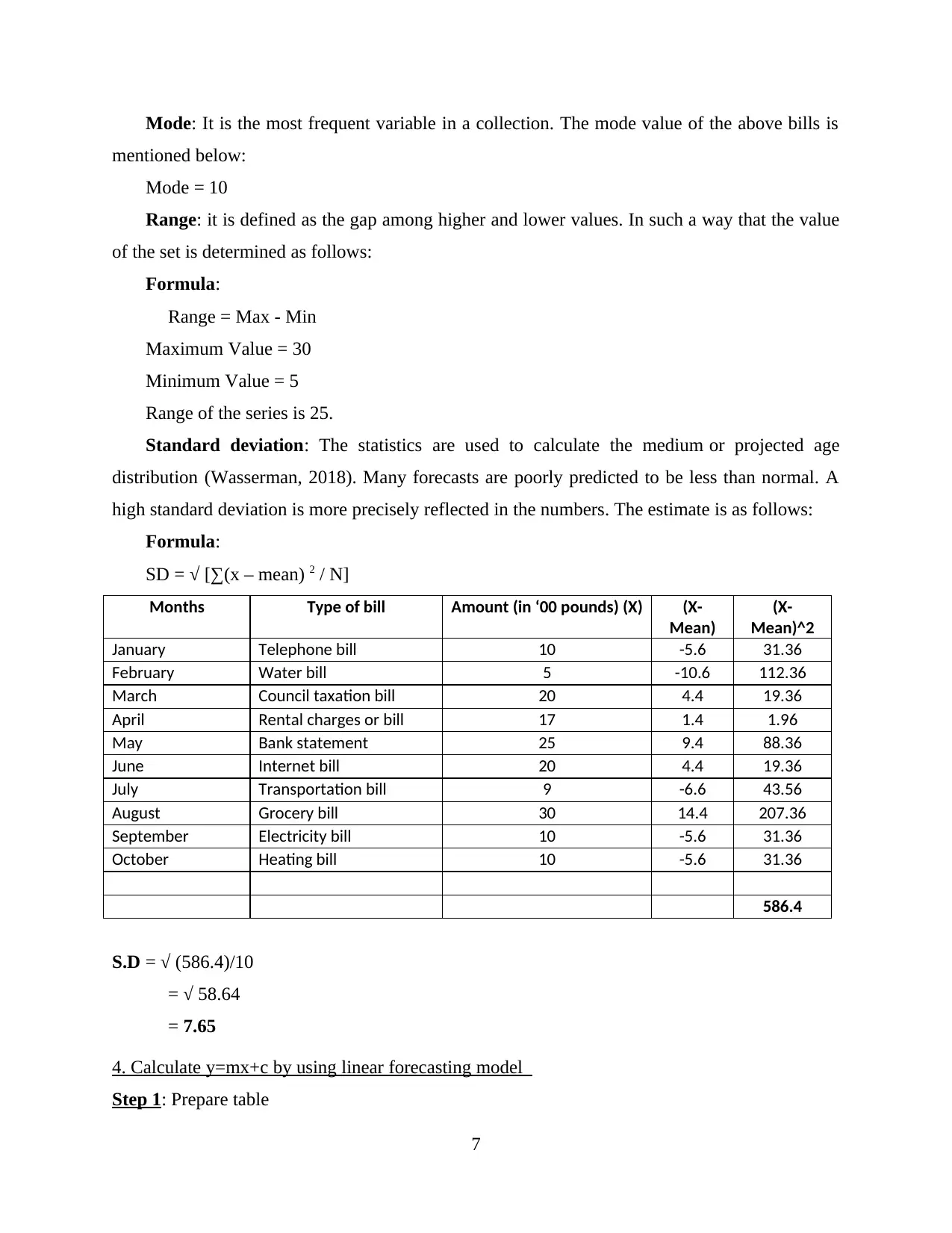
Mode: It is the most frequent variable in a collection. The mode value of the above bills is
mentioned below:
Mode = 10
Range: it is defined as the gap among higher and lower values. In such a way that the value
of the set is determined as follows:
Formula:
Range = Max - Min
Maximum Value = 30
Minimum Value = 5
Range of the series is 25.
Standard deviation: The statistics are used to calculate the medium or projected age
distribution (Wasserman, 2018). Many forecasts are poorly predicted to be less than normal. A
high standard deviation is more precisely reflected in the numbers. The estimate is as follows:
Formula:
SD = √ [∑(x – mean) 2 / N]
Months Type of bill Amount (in ‘00 pounds) (X) (X-
Mean)
(X-
Mean)^2
January Telephone bill 10 -5.6 31.36
February Water bill 5 -10.6 112.36
March Council taxation bill 20 4.4 19.36
April Rental charges or bill 17 1.4 1.96
May Bank statement 25 9.4 88.36
June Internet bill 20 4.4 19.36
July Transportation bill 9 -6.6 43.56
August Grocery bill 30 14.4 207.36
September Electricity bill 10 -5.6 31.36
October Heating bill 10 -5.6 31.36
586.4
S.D = √ (586.4)/10
= √ 58.64
= 7.65
4. Calculate y=mx+c by using linear forecasting model
Step 1: Prepare table
7

Number of months
(X)
Amount (Y) X2 XY
1 10 1 10
2 5 4 10
3 20 9 60
4 17 16 68
5 25 25 125
6 20 36 120
7 9 49 63
8 30 64 240
9 10 81 90
10 10 100 100
∑ 55 ∑ 156 ∑ 385 ∑ 886
Step 2: Calculation of the value of M:
Formula:
M = [ N ∑XY - ∑x ∑y ] / [ N ∑X2 - (∑x)2 ]
= [ 10 * 886 – (55 * 156) ] / [10*385- (55)2 ]
= [8860 – 8580] / [3850 – 3025]
= 280 / 825
= 0.33
Step 3: Calculation of value of C:
Formula: C = {∑y - m ∑x} / N
= (156 – {0.33 * 55}) / 10
= (156 – 18.15) / 10
= 137.85 / 10
= 13.78
Step 4: Number of bill payments on 12th Month:
Formula: Y = mx + c
= 0.33 * 12 + 13.78
= 3.96 + 13.78
= 17.74
Step 5: Number of bill payments on 14th Month:
Formula: Y = mx + c
= 0.33 * 14 + 13.78
8

= 4.62 + 13.78
= 18.4
CONCLUSION
The study indicates that the analysis of data is too critical to evaluate any specific outcome
of compiling data sets. Various types of properties such as mean, mode, median and many more
were determined in this study. In addition the linear equation for estimating the number of bills
payment for the months of 12 and 14.
9

REFERENCES
Books & Journals
Friese, S., 2019. Qualitative data analysis with ATLAS. ti. SAGE Publications Limited.
Landtblom, K. K., 2018. Prospective Teachers’ Conceptions of the Concepts Mean, Median and
Mode. In Students' and Teachers' Values, Attitudes, Feelings and Beliefs in
Mathematics Classrooms (pp. 43-52). Springer, Cham.
Sarkar, J. and Rashid, M., 2016. Visualizing mean, median, mean deviation, and standard
deviation of a set of numbers. The American Statistician. 70(3). pp.304-312.
Wasserman, L., 2018. Topological data analysis. Annual Review of Statistics and Its
Application, 5, pp.501-532.
10