Numeracy and Data Analysis

This project report covers the calculation of mean, mode, median, range, and standard deviation for humidity data in London city. It also includes the presentation of data in table and chart format, as well as the forecasting of humidity using a linear regression model.

NUMERACY AND
DATA ANALYSIS

Table of Contents
INTRODUCTION...........................................................................................................................3
MAIN BODY...................................................................................................................................3
1. Arrangement of data in table format........................................................................................3
2. Presentation of data in two charts............................................................................................3
3. Calculation of below mentioned items:...................................................................................5
4. Calculating values of m, c and humidity forecast of day 15 and 20........................................7
CONCLUSION................................................................................................................................8
REFERENCES................................................................................................................................9

INTRODUCTION
Data analysis is a type of framework that is linked with process of collecting and
analysing financial data with an aim of taking suitable decisions (Mulligan, 2015). There are
different kinds of techniques for making effective analysis of data. The project report covers
detailed information regards to calculation of mean-mode-median in accordance of humidity data
of London city of ten days (Humidity data of London, 2019). As well as report includes
implementation of linear regression model for forecasting of humidity percentage in further days.
MAIN BODY
1. Arrangement of data in table format.
The data of humidity percentage of London city of ten days (21st of October to 30th of
October) is being presented in table format in such manner:
Serial number Date Humidity (in terms of %)
1 21st of October, 2019 88
2 22nd of October, 2019 94
3 23rd of October, 2019 95
4 24th of October, 2019 96
5 25th of October, 2019 96
6 26th of October, 2019 79
7 27th of October, 2019 93
8 28th of October, 2019 98
9 29th of October, 2019 82
10 30th of October, 2019 82

2. Presentation of data in two charts.
Bar chart- This can be defined as a kinds of diagram in that monetary data are presented in form
of horizontal bars. Herein, below presentation of humidity data has been done in form of bar
chart in such manner:
21st of October, 2019
22nd of October, 2019
23rd of October, 2019
24th of October, 2019
25th of October, 2019
26th of October, 2019
27th of October, 2019
28th of October, 2019
29th of October, 2019
30th of October, 2019
0 20 40 60 80 100 120
88
94
95
96
96
79
93
98
82
82
Humidity (in terms of %)
Column chart- This is defined as a type of diagram in which financial data is presented in the
way of vertical lines (.Estrada-Mejia, de Vries and Zeelenberg, 2016). Herein, below
presentation of humidity data has been done in form of column chart in such manner:

21st of October, 2019
22nd of October, 2019
23rd of October, 2019
24th of October, 2019
25th of October, 2019
26th of October, 2019
27th of October, 2019
28th of October, 2019
29th of October, 2019
30th of October, 2019
0
20
40
60
80
100
120
88 94 95 96 96
79
93 98
82 82
Humidity (in terms of %)
3. Calculation of below mentioned items:
Date Humidity (in terms of %)
21st of October, 2019 88
22nd of October, 2019 94
23rd of October, 2019 95
24th of October, 2019 96
25th of October, 2019 96
26th of October, 2019 79
27th of October, 2019 93
28th of October, 2019 98
29th of October, 2019 82
30th of October, 2019 82
Total 903
Mean 90.3
Mode 82
Median 93.5
Range 19
Standard deviation 6.98

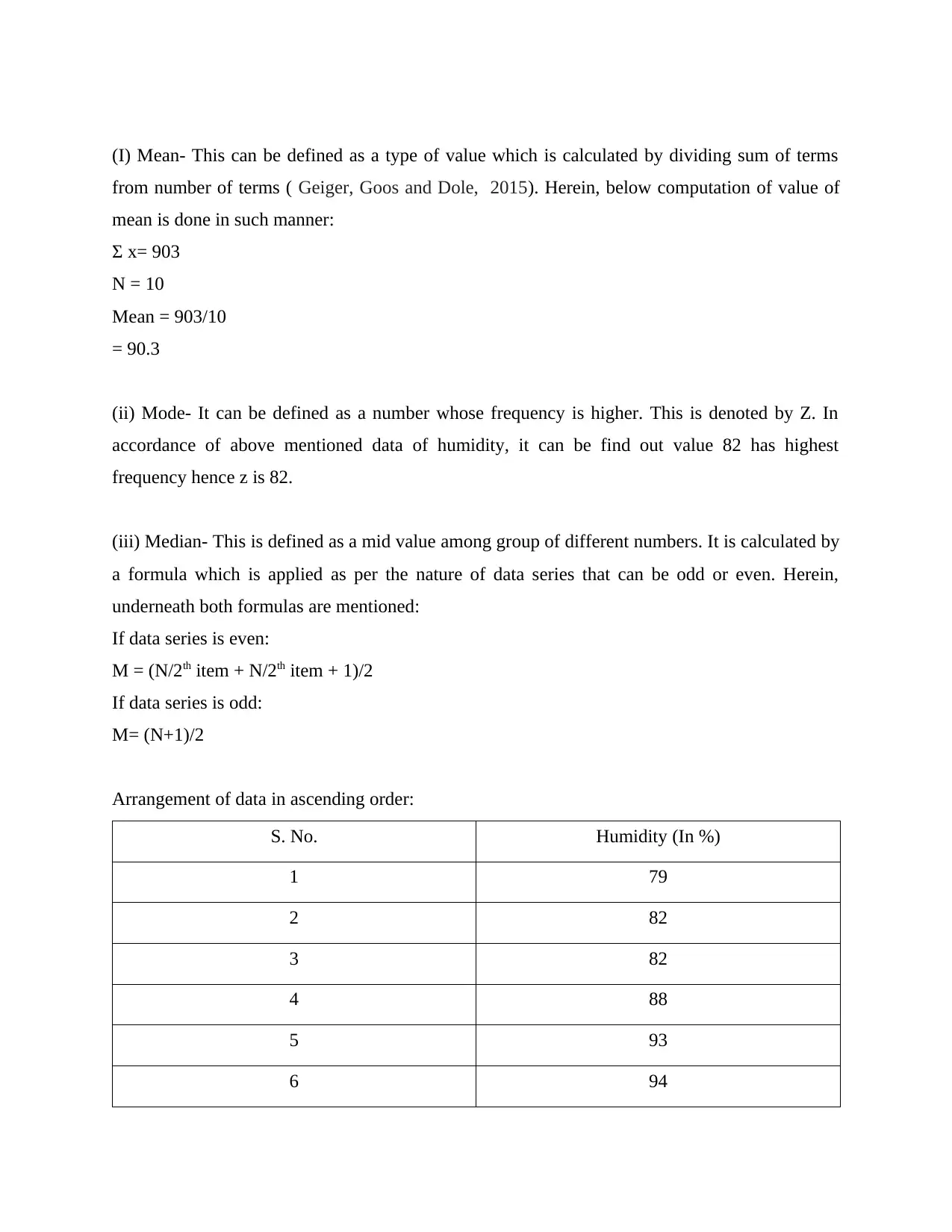
(I) Mean- This can be defined as a type of value which is calculated by dividing sum of terms
from number of terms ( Geiger, Goos and Dole, 2015). Herein, below computation of value of
mean is done in such manner:
Σ x= 903
N = 10
Mean = 903/10
= 90.3
(ii) Mode- It can be defined as a number whose frequency is higher. This is denoted by Z. In
accordance of above mentioned data of humidity, it can be find out value 82 has highest
frequency hence z is 82.
(iii) Median- This is defined as a mid value among group of different numbers. It is calculated by
a formula which is applied as per the nature of data series that can be odd or even. Herein,
underneath both formulas are mentioned:
If data series is even:
M = (N/2th item + N/2th item + 1)/2
If data series is odd:
M= (N+1)/2
Arrangement of data in ascending order:
S. No. Humidity (In %)
1 79
2 82
3 82
4 88
5 93
6 94

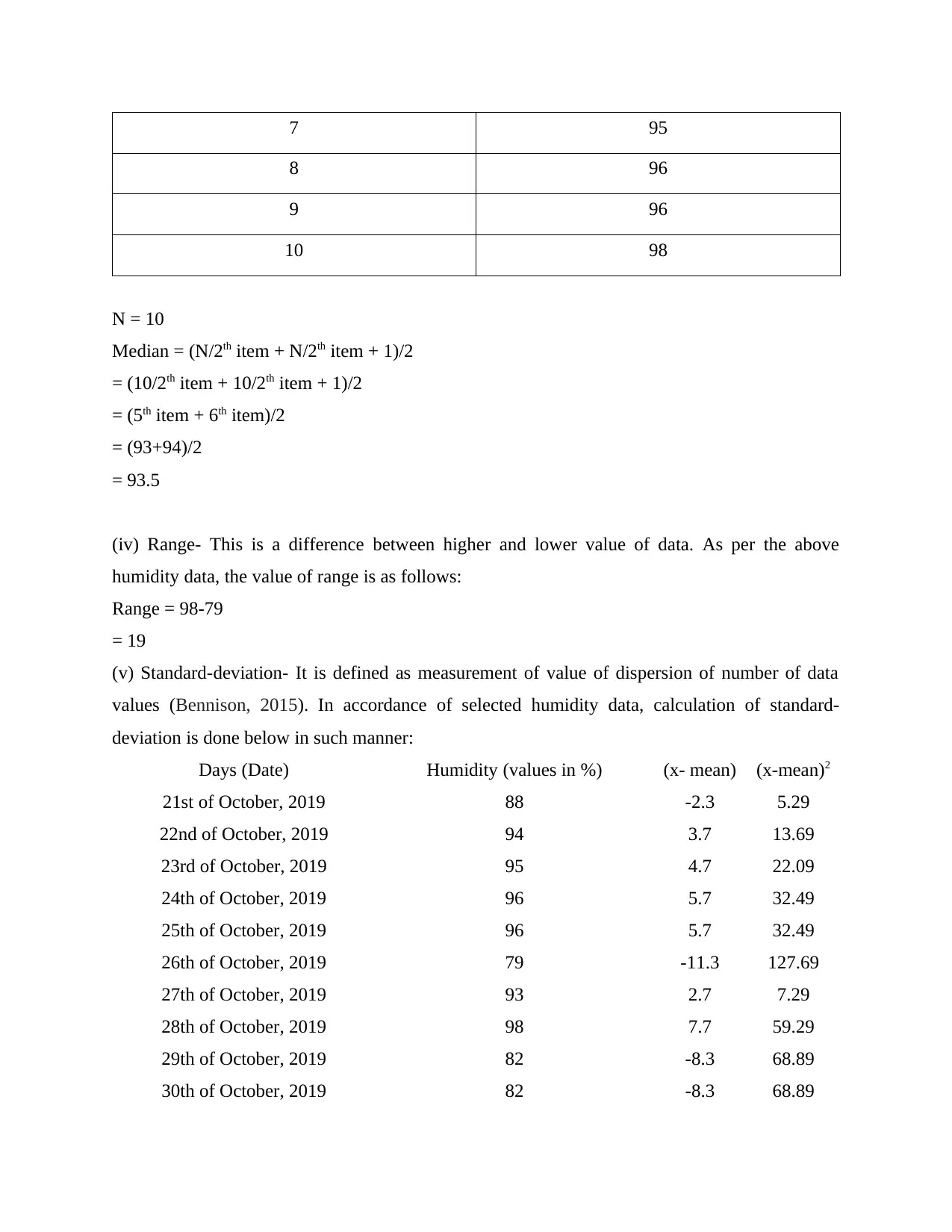
7 95
8 96
9 96
10 98
N = 10
Median = (N/2th item + N/2th item + 1)/2
= (10/2th item + 10/2th item + 1)/2
= (5th item + 6th item)/2
= (93+94)/2
= 93.5
(iv) Range- This is a difference between higher and lower value of data. As per the above
humidity data, the value of range is as follows:
Range = 98-79
= 19
(v) Standard-deviation- It is defined as measurement of value of dispersion of number of data
values (Bennison, 2015). In accordance of selected humidity data, calculation of standard-
deviation is done below in such manner:
Days (Date) Humidity (values in %) (x- mean) (x-mean)2
21st of October, 2019 88 -2.3 5.29
22nd of October, 2019 94 3.7 13.69
23rd of October, 2019 95 4.7 22.09
24th of October, 2019 96 5.7 32.49
25th of October, 2019 96 5.7 32.49
26th of October, 2019 79 -11.3 127.69
27th of October, 2019 93 2.7 7.29
28th of October, 2019 98 7.7 59.29
29th of October, 2019 82 -8.3 68.89
30th of October, 2019 82 -8.3 68.89

Total=
438.1
Variance = [ ∑(x – mean)2 / N ]
= 438.1/10
= 43.81
Standard deviation = √variance
= √43.81
= 6.62
4. Calculating values of m, c and humidity forecast of day 15 and 20.
Days (X) Humidity (Y) X2 ∑XY Y2
1 88 1 88 7744
2 94 4 188 8836
3 95 9 285 9025
4 96 16 384 9216
5 96 25 480 9216
6 79 36 474 6241
7 93 49 651 8649
8 98 64 784 9604
9 82 81 738 6724
10 82 100 820 6724
∑X= 55 ∑Y= 903 ∑X2= 385 ∑XY= 4892 ∑Y2 = 81979
(I) Calculation of value of m:
m= (∑Y)(∑X2)- (∑X)(∑XY) / n(∑X2)-(∑X)2
= 903*385-55*4892 / 10*385-(55) 2
= 347655- 269060/ 3850-3025
= 78595/825
= 95.26

(ii) Calculation of value of c:
c= n(∑XY)- (∑X)(∑Y) / n(∑X2)-(∑X)2
= 10*4892-55*903 / 10*385-(55) 2
= 48920-49665/ 3850-3025
= -745/825
= -0.90
(iii) Forecasting of humidity:
For 15th day-
Y = m+cx
= 95.26+ (-0.90*15)
= 95.26+ (-13.54)
= 81.72%
For 20th day-
= 95.26+(-0.90*20)
= 95.26+ (-18)
= 77.26%
CONCLUSION
On the basis of above project report, it can be concluded that any type of business entity
can take suitable decisions as per the analysed data. In the absence of proper data analysis, it may
difficult to take corrective actions. Report concludes vital range of calculations such as mean-
mode-median as per humidity data of London city. In the end part of report, forecasting of
humidity is done by help of linear regression model.

REFERENCES
Books and journal:
Mulligan, J., 2015. Moving beyond basic numeracy: data modeling in the early years of
schooling. ZDM. 47(4). pp.653-663.
Estrada-Mejia, C., de Vries, M. and Zeelenberg, M., 2016. Numeracy and wealth. Journal of
Economic Psychology. 54. pp.53-63.
Geiger, V., Goos, M. and Dole, S., 2015. The role of digital technologies in numeracy teaching
and learning. International Journal of Science and Mathematics Education. 13(5).
pp.1115-1137.
Bennison, A., 2015. Supporting teachers to embed numeracy across the curriculum: A
sociocultural approach. ZDM. 47(4). pp.561-573.
Online
Humidity data of London. 2019. [Online]. Available through:
<https://www.timeanddate.com/weather/uk/london/historic>