Numeracy and Data Analysis

This document discusses numeracy and data analysis, covering topics such as presenting expenditure data, using charts, calculating mean, mode, median, range, and standard deviation, and using a linear forecasting model. It provides insights into the importance of data analysis in making informed decisions.

Numeracy and Data Analysis

Contents
INTRODUCTION...........................................................................................................................3
MAIN BODY..................................................................................................................................3
1. Presentation of selected expenditure data in tabular form:......................................................3
2. Presenting selected data of expenses with help of two different charts:.................................3
3. Calculate and discuss the followings:......................................................................................5
4. Linear forecasting model which is y = mx + c:.......................................................................8
CONCLUSION..............................................................................................................................10
REFERENCES..............................................................................................................................11

INTRODUCTION
Data analysis corresponds to data evaluation, inspection, transition, and processing
mechanism that aims to uncover crucial information inform findings, and assists in decisions.
Data analysis processes has various characteristics and methods, underneath number of labels
containing multiple tactics, and is employed in various fields of business, studies, and social
research. Data analysis serves a part in taking more rational decisions in contemporary’s
business environment and enabling entities run more smoothly (Miles, Huberman and Saldaña,
2018). The study-assessment encompasses different data analysis-related principles such as
the standard deviation, mode, mean formula, median etc. with the 10 consecutive
months' expenditure data. In addition, the report covers linear forecasting method to estimate
expenditures for month eleven and twelve.
MAIN BODY
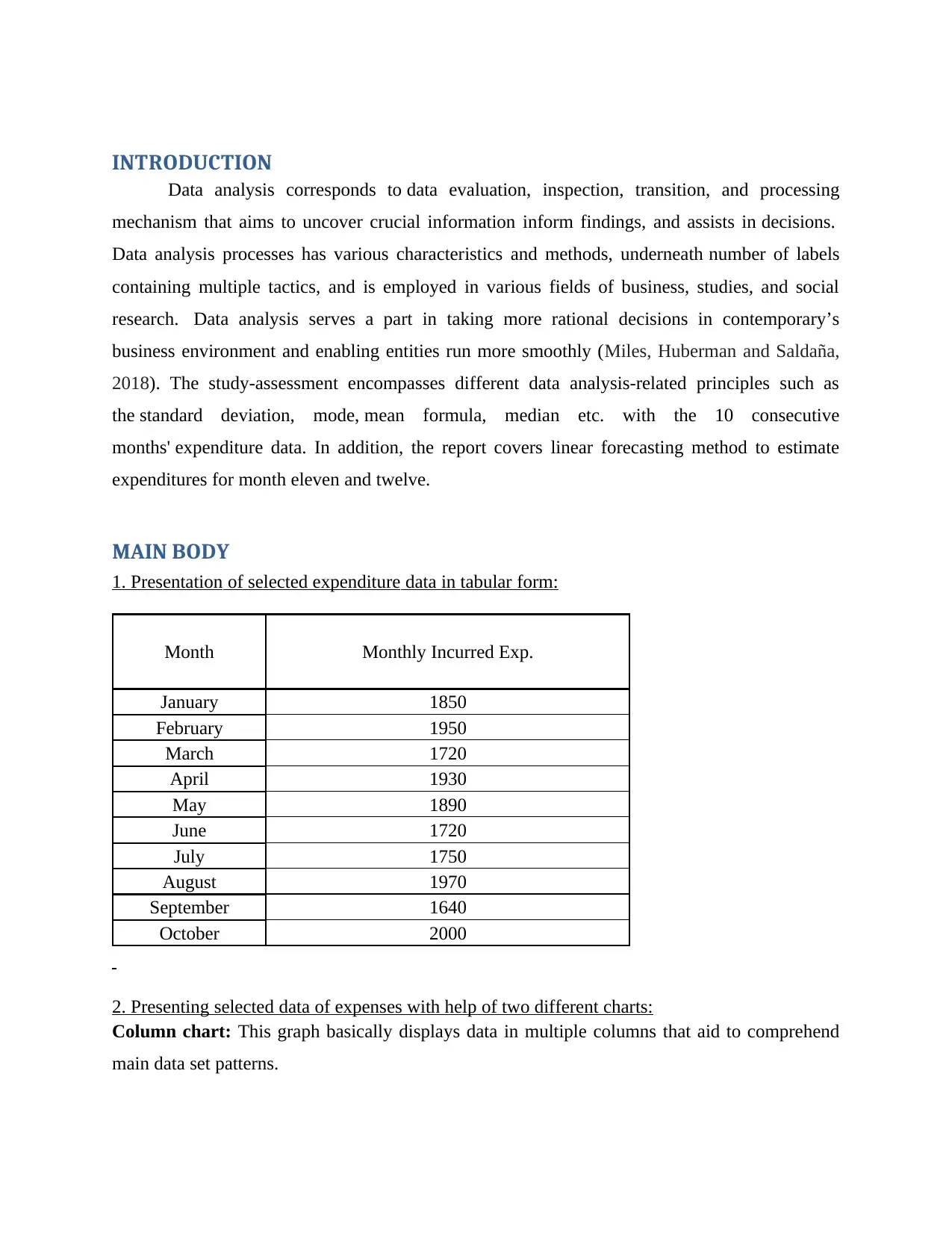
1. Presentation of selected expenditure data in tabular form:
Month Monthly Incurred Exp.
January 1850
February 1950
March 1720
April 1930
May 1890
June 1720
July 1750
August 1970
September 1640
October 2000
2. Presenting selected data of expenses with help of two different charts:
Column chart: This graph basically displays data in multiple columns that aid to comprehend
main data set patterns.

Jan Feb MarchApril May June July Aug Sep
0
500
1000
1500
2000
2500
1850 1950
1720
1930 1890
1720 1750
1970
1640
Monthly incurred Exp.
Monthly incurred Exp.
Bar chart: Horizontal columns are employed in this graph to describe the data collection. A axis
exhibits attributes to be displayed on bars, whereas others represent data series such as months
for our scenario.
Jan
Feb
March
April
May
June
July
Aug
Sep
Oct
0 500 1000 1500 2000 2500
1850
1950
1720
1930
1890
1720
1750
1970
1640
2000
Monthly incurred Exp.
Monthly incurred Exp.

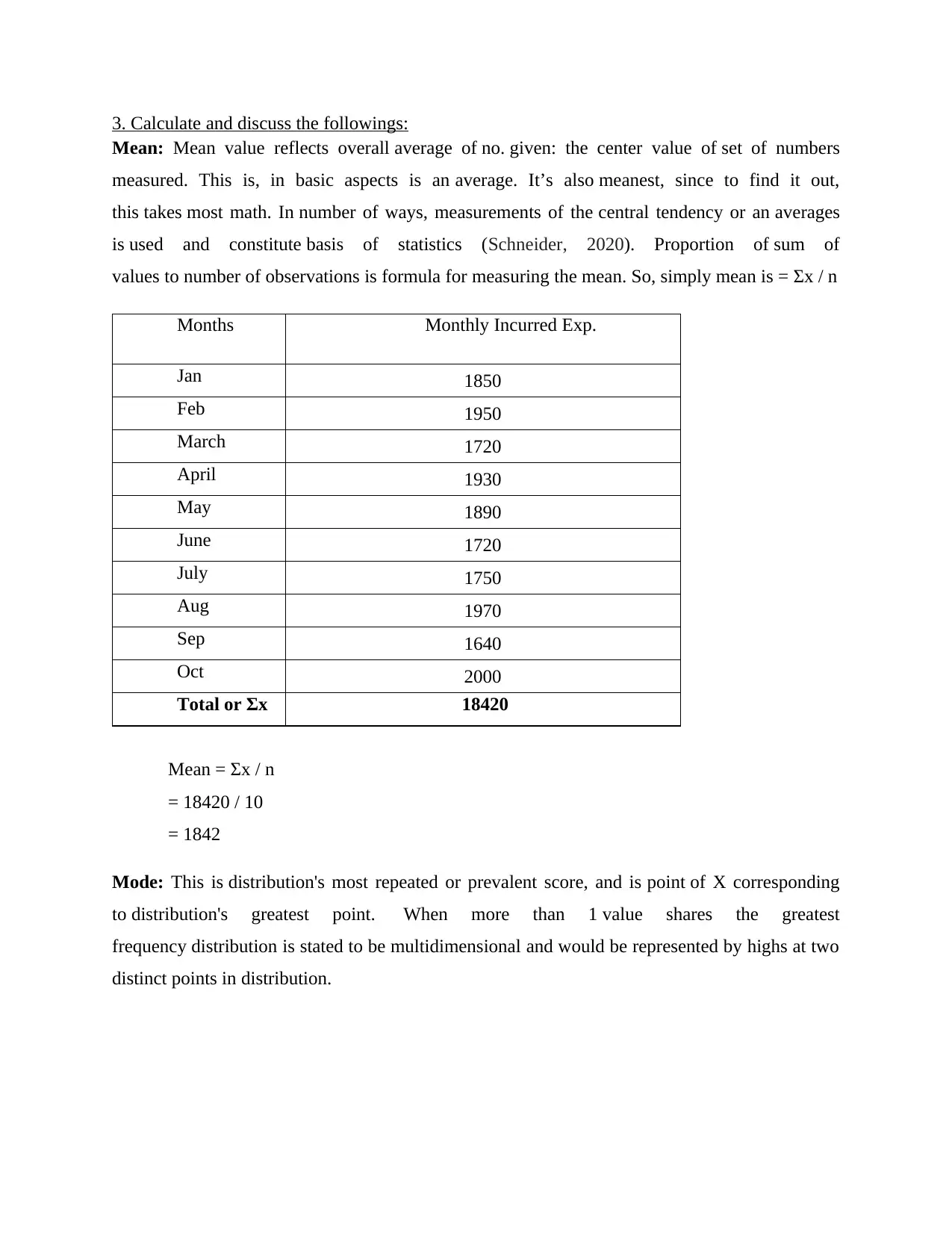
3. Calculate and discuss the followings:
Mean: Mean value reflects overall average of no. given: the center value of set of numbers
measured. This is, in basic aspects is an average. It’s also meanest, since to find it out,
this takes most math. In number of ways, measurements of the central tendency or an averages
is used and constitute basis of statistics (Schneider, 2020). Proportion of sum of
values to number of observations is formula for measuring the mean. So, simply mean is = Σx / n
Months Monthly Incurred Exp.
Jan 1850
Feb 1950
March 1720
April 1930
May 1890
June 1720
July 1750
Aug 1970
Sep 1640
Oct 2000
Total or Σx 18420
Mean = Σx / n
= 18420 / 10
= 1842
Mode: This is distribution's most repeated or prevalent score, and is point of X corresponding
to distribution's greatest point. When more than 1 value shares the greatest
frequency distribution is stated to be multidimensional and would be represented by highs at two
distinct points in distribution.

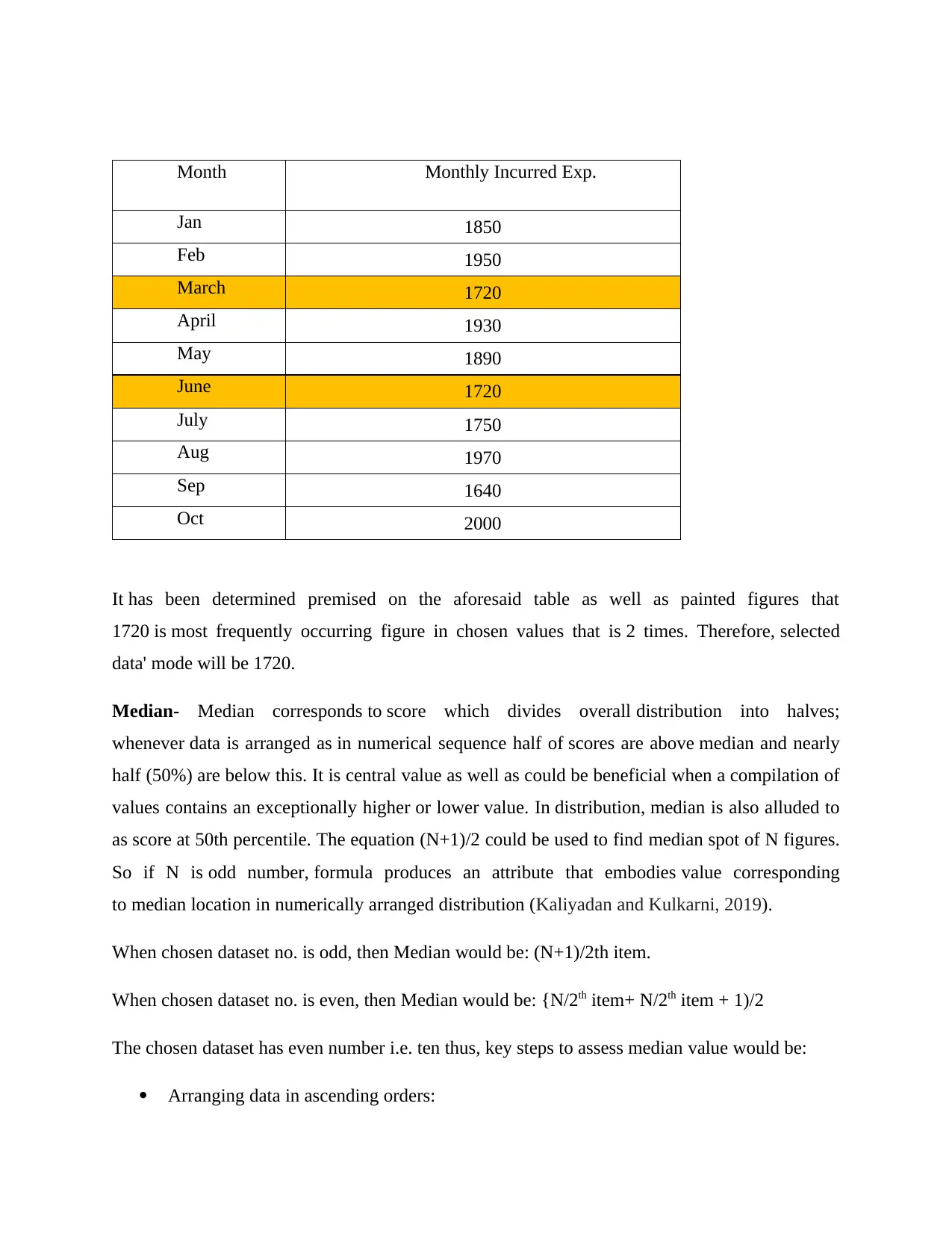
Month Monthly Incurred Exp.
Jan 1850
Feb 1950
March 1720
April 1930
May 1890
June 1720
July 1750
Aug 1970
Sep 1640
Oct 2000
It has been determined premised on the aforesaid table as well as painted figures that
1720 is most frequently occurring figure in chosen values that is 2 times. Therefore, selected
data' mode will be 1720.
Median- Median corresponds to score which divides overall distribution into halves;
whenever data is arranged as in numerical sequence half of scores are above median and nearly
half (50%) are below this. It is central value as well as could be beneficial when a compilation of
values contains an exceptionally higher or lower value. In distribution, median is also alluded to
as score at 50th percentile. The equation (N+1)/2 could be used to find median spot of N figures.
So if N is odd number, formula produces an attribute that embodies value corresponding
to median location in numerically arranged distribution (Kaliyadan and Kulkarni, 2019).
When chosen dataset no. is odd, then Median would be: (N+1)/2th item.
When chosen dataset no. is even, then Median would be: {N/2th item+ N/2th item + 1)/2
The chosen dataset has even number i.e. ten thus, key steps to assess median value would be:
 Arranging data in ascending orders:

Month Monthly Incurred Exp.
Sep 1640
March 1720
June 1720
July 1750
Jan 1850
May 1890
April 1930
Feb 1950
Aug 1970
Oct 2000
 N= 10
 M= (10/2th item + 10/2th item + 1)/2
 = (5th item+ 6th item)/2
 = (1850 + 1890)/2
 = 3740 / 2
 = 1870
Range: Range is distinction between distribution's maximum and low value. This is not always
employed as sole variability indicator since it is focused exclusively on distribution's most severe
points and doesn't represent the variance trend within distribution.
Higher value = 2000
Lower value = 1640
Range= (2000 -1640)
= 360
Standard deviation: Standard deviation gives insight into extent of variance within a set of
attributes It evaluates deviation from mean of group (average). The positive value square root
of variance is standard deviation. Variance of square units is metric and has minimal significance
with regard to the results Thereby, measure of variability represented in same units as data

is standard deviation. SD of such deviations is quite much like mean or average (Amrhein,
Trafimow and Greenland, 2019).
Month Expenses
(x)
x- mean (x-
mean)2
Jan 1850 8 64
Feb 1950 108 11664
March 1720 -122 14884
April 1930 88 7744
May 1890 48 2304
June 1720 -122 14884
July 1750 -92 8464
Aug 1970 128 16384
Sep 1640 -202 40804
Oct 2000 158 24964
∑x = 18420 ∑(x – mean)
2 =
142160
Mean = Σx / n = 1842
Variance = (x-mean)2/n = 142160
Sd = √(x-mean)2/n = 119.2309
4. Linear forecasting model which is y = mx + c:
Calculation of value m:
Month (x) Expenses (y) x2 xy
1 1850 1 1850
2 1950 4 3900
3 1720 9 5160
4 1930 16 7720
5 1890 25 9450
6 1720 36 10320
7 1750 49 12250
8 1970 64 15760

9 1640 81 14760
10 2000 100 20000
Σx = 55 Σy = 18420 Σx2 = 385 Σxy = 101170
y = mx + c
Here,
m= n (∑xy) - (∑x) (∑y)/ n(∑x2)-( ∑x)2
= 10*(101170)-(55)*(18420)/10*(385)-(55) 2
= 1011700-1013100/3850-3025
= 1400/825
= 1.6970
Calculation of c:
c = [(∑y) / n]-m (∑x/n)
= [18420/10]- 1.6970 (55/10)
= 1842-9.3333
= 1832.667
Forecasting for month 11 and 12:
Forecasting for month 11:
y = mx + c
= 1.6970 * 11 + 1832.667
= 1851.334 or 1850
Forecasting for month 12:
= 1.6970 * 12 + 1832.667
= 1853.03 or around 1853

CONCLUSION
The above study asserts that the data analysis is characterized as a method of organizing
integrating and presenting data to provide beneficial business decision-making details. The
predominant object of this study is to observe the results data through useful insights and to
make the appropriate decisions with respect to possible issues.

REFERENCES
Books and journal:
Miles, M.B., Huberman, A.M. and Saldaña, J., 2018. Qualitative data analysis: A methods
sourcebook. Sage publications.
Schneider, J., 2020. New definitions (measures) of skewness, mean and dispersion of fuzzy
numbers--by way of a new representation as parameterized curves. arXiv preprint
arXiv:2011.01041.
Kaliyadan, F. and Kulkarni, V., 2019. Types of variables, descriptive statistics, and sample
size. Indian dermatology online journal, 10(1), p.82.
Amrhein, V., Trafimow, D. and Greenland, S., 2019. Inferential statistics as descriptive statistics:
There is no replication crisis if we don’t expect replication. The American
Statistician, 73(sup1), pp.262-270.