Numeracy and Data Analysis

This document provides information on numeracy and data analysis. It includes topics such as arranging data in table format, presenting data in charts, calculating mean, median, mode, range, and standard deviation, and using linear regression for calculations. It also includes references for further reading.

Numeracy
and
Data Analysis

Table of Contents
1. Arrange the data in table format..................................................................................................3
2. Present the data in column chart and line chart...........................................................................3
3. Calculation of mean, median, mode, range and standard deviation............................................4
I. Mean:........................................................................................................................................4
II. Median:...................................................................................................................................5
III. Mode:.....................................................................................................................................6
IV. Range:....................................................................................................................................6
V. Standard deviation:.................................................................................................................7
4. Calculation based on y = mx + c.................................................................................................8
I. Calculation of m.......................................................................................................................9
II. Calculation of c.......................................................................................................................9
III. Calculation for 12th and 14th day expenses.............................................................................9
REFERENCES..............................................................................................................................10

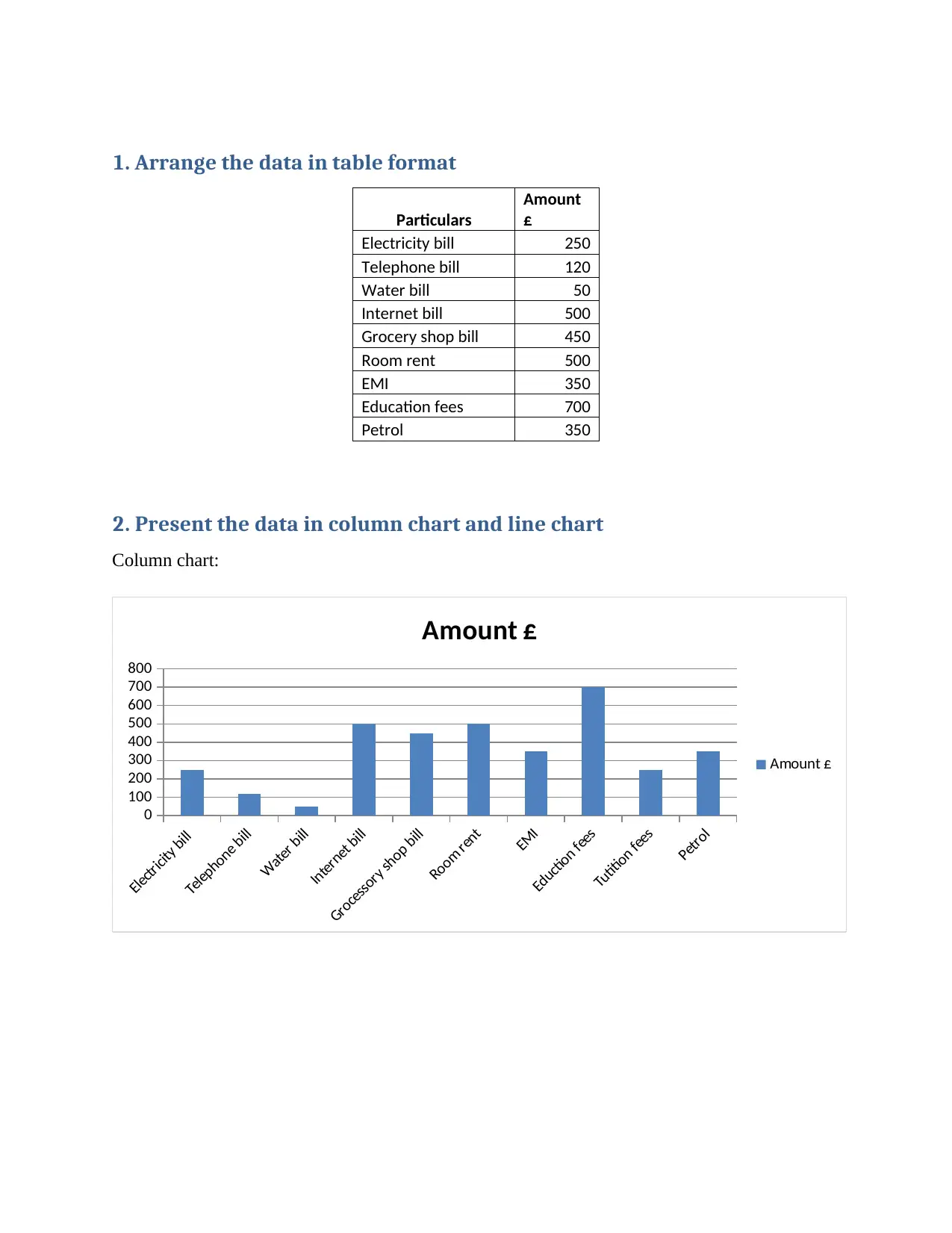
1. Arrange the data in table format
Particulars
Amount
£
Electricity bill 250
Telephone bill 120
Water bill 50
Internet bill 500
Grocery shop bill 450
Room rent 500
EMI 350
Education fees 700
Petrol 350
2. Present the data in column chart and line chart
Column chart:
Electricity bill
Telephone bill
Water bill
Internet bill
Grocessory shop bill
Room rent
EMI
Eduction fees
Tutition fees
Petrol
0
100
200
300
400
500
600
700
800
Amount £
Amount £

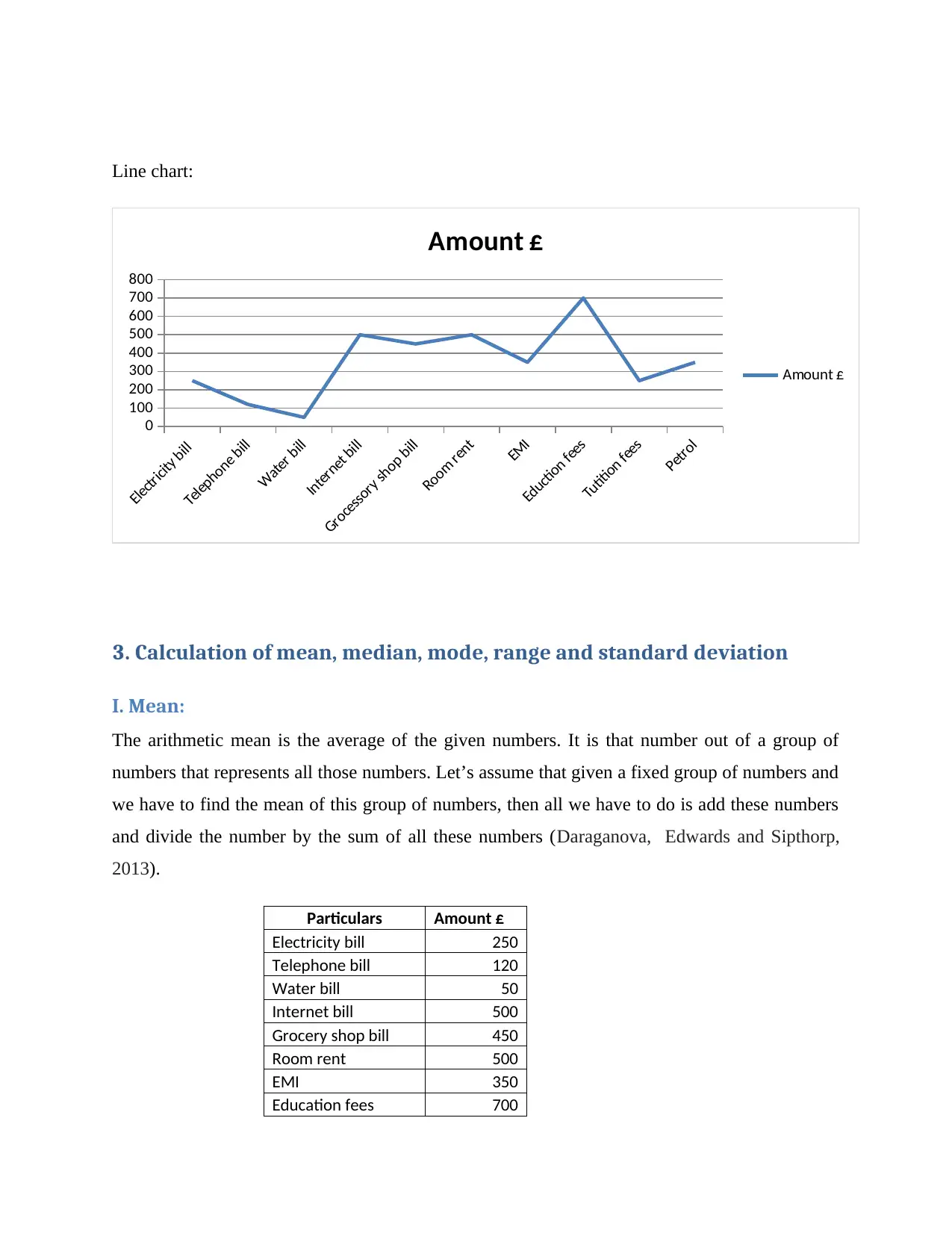
Line chart:
Electricity bill
Telephone bill
Water bill
Internet bill
Grocessory shop bill
Room rent
EMI
Eduction fees
Tutition fees
Petrol
0
100
200
300
400
500
600
700
800
Amount £
Amount £
3. Calculation of mean, median, mode, range and standard deviation
I. Mean:
The arithmetic mean is the average of the given numbers. It is that number out of a group of
numbers that represents all those numbers. Let’s assume that given a fixed group of numbers and
we have to find the mean of this group of numbers, then all we have to do is add these numbers
and divide the number by the sum of all these numbers (Daraganova, Edwards and Sipthorp,
2013).
Particulars Amount £
Electricity bill 250
Telephone bill 120
Water bill 50
Internet bill 500
Grocery shop bill 450
Room rent 500
EMI 350
Education fees 700

Tuition fees 250
Petrol 350
Sum Ʃ 3520
Mean =x̄ Sum Ʃ / Number of items
Mean =x̄ 352
II. Median:
If we say in simple language, the median is the number that falls exactly in between the given
numbers. This is the number that separates the larger part of this group from the smaller part of
the group. It can be called the medium part of a given population. To remove the median we
have to arrange the numbers in different ways. For example, if we have to find the median of
some numbers, we will either have to write it in increasing order or we will have to write it in
decreasing order. When we arrange these numbers in such a way, then the number between them
will be the median of these numbers (Groves, Mousley and Forgasz, 2006).
Particulars Amount £
Water bill 50
Telephone bill 120
Electricity bill 250
Tuition fees 250
EMI 350
Petrol 350
Grocery shop bill 450
Internet bill 500
Room rent 500
Education fees 700
Median = {(n + 1) ÷ 2}th value
Median = { (10 + 1) /2 }
Median = 5.5
Average = (middle value before + middle value after) ÷ 2
(5th + 6th value) /2
(350 + 350)/2
Median = 350

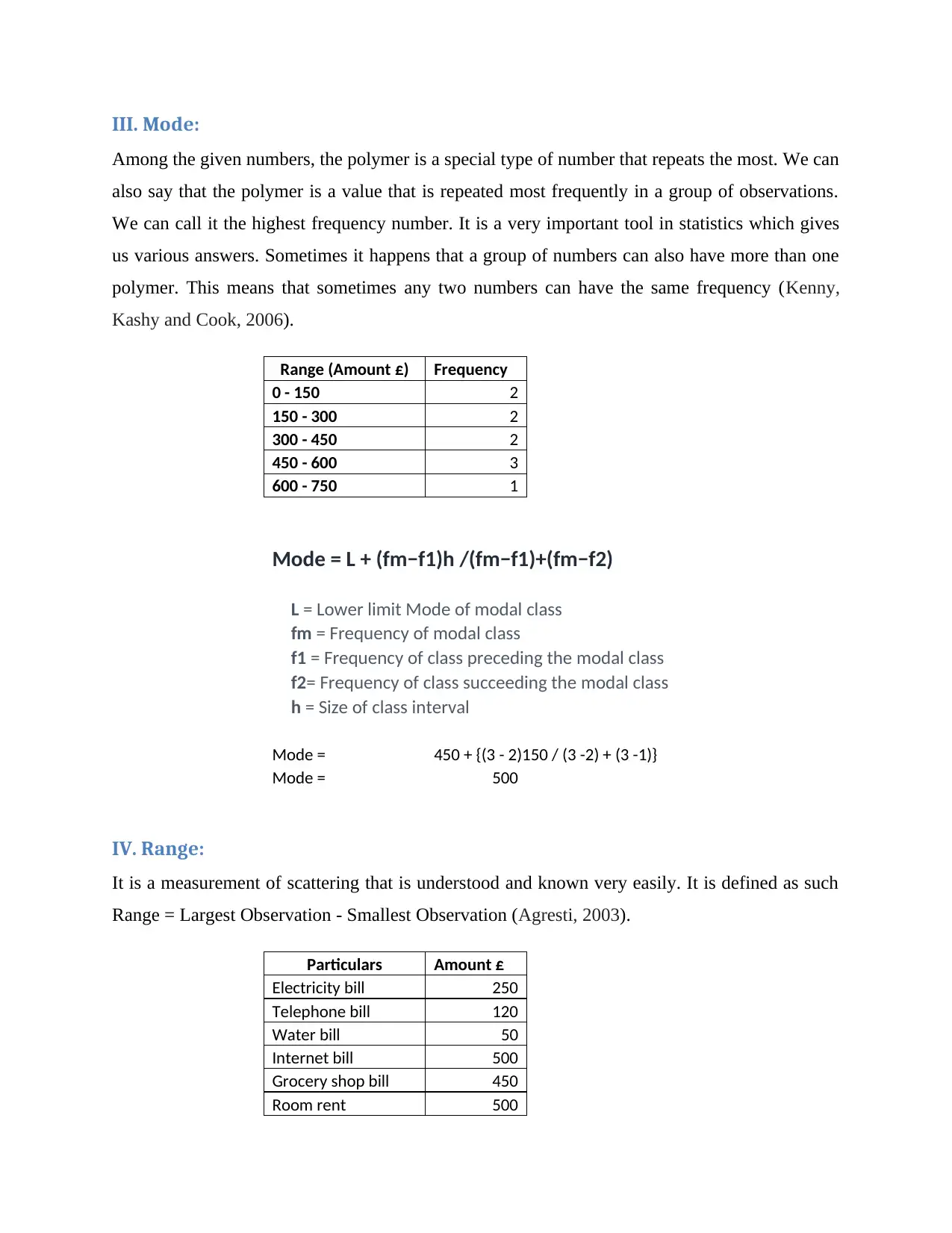
III. Mode:
Among the given numbers, the polymer is a special type of number that repeats the most. We can
also say that the polymer is a value that is repeated most frequently in a group of observations.
We can call it the highest frequency number. It is a very important tool in statistics which gives
us various answers. Sometimes it happens that a group of numbers can also have more than one
polymer. This means that sometimes any two numbers can have the same frequency (Kenny,
Kashy and Cook, 2006).
Range (Amount £) Frequency
0 - 150 2
150 - 300 2
300 - 450 2
450 - 600 3
600 - 750 1
Mode = L + (fm−f1)h /(fm−f1)+(fm−f2)
L = Lower limit Mode of modal class
fm = Frequency of modal class
f1 = Frequency of class preceding the modal class
f2= Frequency of class succeeding the modal class
h = Size of class interval
Mode = 450 + {(3 - 2)150 / (3 -2) + (3 -1)}
Mode = 500
IV. Range:
It is a measurement of scattering that is understood and known very easily. It is defined as such
Range = Largest Observation - Smallest Observation (Agresti, 2003).
Particulars Amount £
Electricity bill 250
Telephone bill 120
Water bill 50
Internet bill 500
Grocery shop bill 450
Room rent 500

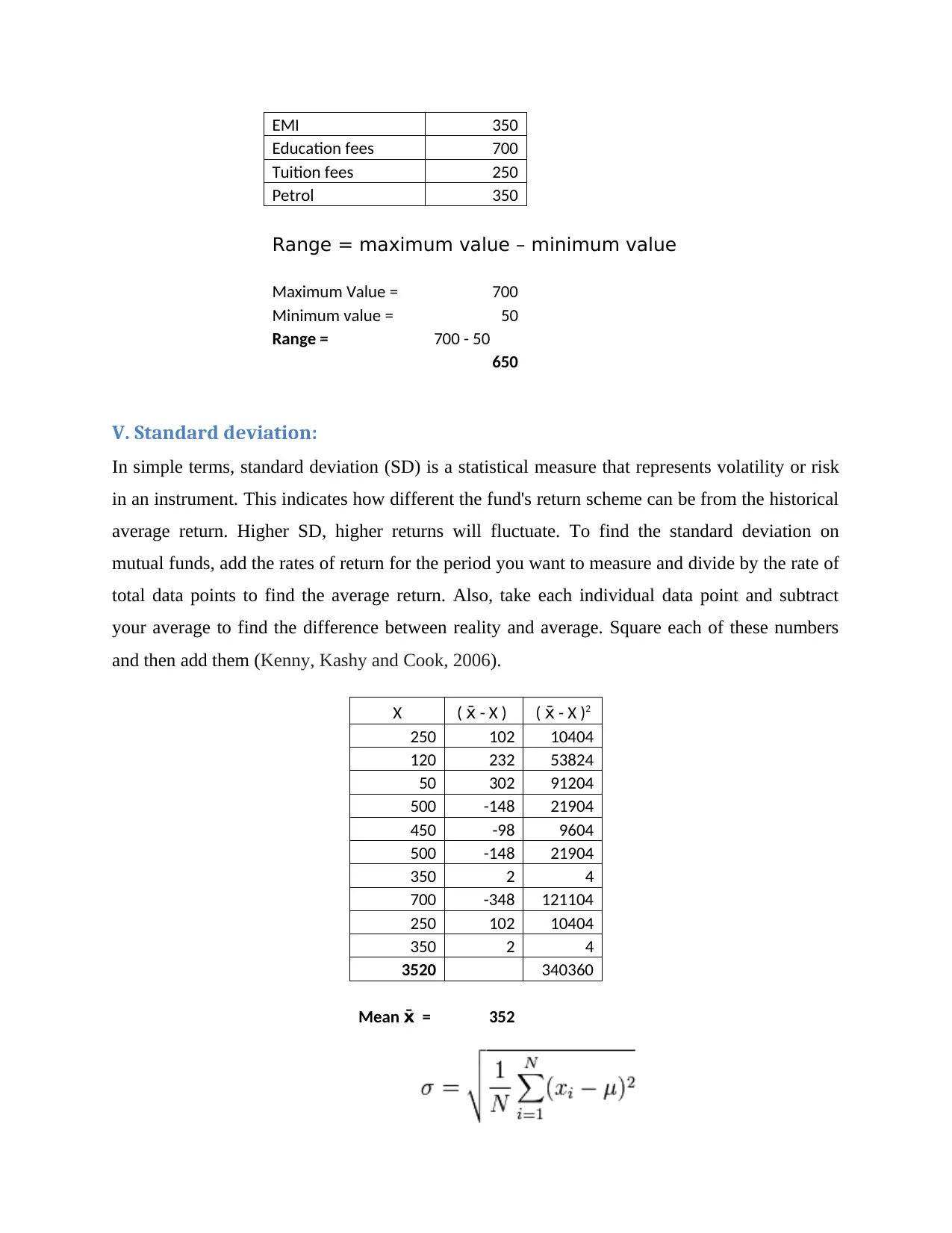
EMI 350
Education fees 700
Tuition fees 250
Petrol 350
Range = maximum value – minimum value
Maximum Value = 700
Minimum value = 50
Range = 700 - 50
650
V. Standard deviation:
In simple terms, standard deviation (SD) is a statistical measure that represents volatility or risk
in an instrument. This indicates how different the fund's return scheme can be from the historical
average return. Higher SD, higher returns will fluctuate. To find the standard deviation on
mutual funds, add the rates of return for the period you want to measure and divide by the rate of
total data points to find the average return. Also, take each individual data point and subtract
your average to find the difference between reality and average. Square each of these numbers
and then add them (Kenny, Kashy and Cook, 2006).
X ( - X )x̄ ( - X )x̄ 2
250 102 10404
120 232 53824
50 302 91204
500 -148 21904
450 -98 9604
500 -148 21904
350 2 4
700 -348 121104
250 102 10404
350 2 4
3520 340360
Mean =x̄ 352

Standard deviation = 184.48
4. Calculation based on y = mx + c
LINEAR FORECASTING MODEL: Linear regression analysis establishes a relationship
between a dependent variable and one or more independent variables. Simple linear regression
has only one independent variable. The dependent variable is also what you want to predict.
Once the values of A and B are calculated, any future value of X can be substituted to predict the
corresponding value of Y (Gelman and et.al., 2013).
Exponential adjustment: It also establishes a relationship between a dependent variable and one
or more independent variables. The uniform (exponential) curve in this allows a better fit than a
straight line (Hair and et.al., 1998).
y = mx + c
y = how far up
x = how far along
m = Slope or Gradient (how steep the line is)
c = value of y when x=0
I. Calculation of m
m = Change in Y/ Change in X
X Y
1 50

2 120
3 250
4 250
5 350
6 350
7 450
8 500
9 500
10 700
m = 120 - 50/2-1
m = 70
II. Calculation of c
Y = mx + c
120 = 70(2) + c
C = 120 – 140
C = -20
III. Calculation for 12th and 14th day expenses
X = 12
Y = mx + c
Y = 70(12) + (-20)
= 840 – 20
= 820
X = 14
Y = mx + c
= 70(14) + (-20)
= 980 – 20
= 960
Hence, on 12th day the expenses will be £820 and on 14th day it will be £960.

REFERENCES
Books
Agresti, A., 2003. Categorical data analysis (Vol. 482). John Wiley & Sons.
Daraganova, G., Edwards, B. and Sipthorp, M., 2013. Using National Assessment Program
Literacy and Numeracy (NAPLAN) Data in the Longitudinal Study of Australian Children
(LSAC). Department of Families, Housing, Community Services and Indigenous Affairs.
Gelman, A., and et.al., 2013. Bayesian data analysis. CRC press.
Groves, S., Mousley, J. and Forgasz, H., 2006. A primary numeracy: a mapping review and
analysis of Australian research in numeracy learning at the primary school level: report.
Centre for Studies in Mathematics, Science and Environmental Education, Deakin
University.
Hair, J.F., and et.al., 1998. Multivariate data analysis (Vol. 5, No. 3, pp. 207-219). Upper Saddle
River, NJ: Prentice hall.
Kenny, D.A., Kashy, D.A. and Cook, W.L., 2006. Dyadic data analysis. Guilford press.