Numeracy and Data Analysis - Desklib

This study material covers Numeracy and Data Analysis with topics like Arranging Data, Charts depicting data, Calculation with steps, Linear forecasting and more. It also includes mean, median, mode, range and standard deviation calculation with steps.

NUMERACY AND DATA
ANALYSIS

TABLE OF CONTENTS
TASK...............................................................................................................................................2
Arranging Data............................................................................................................................2
Charts depicting data...................................................................................................................2
Calculation with steps..................................................................................................................3
Linear forecasting........................................................................................................................5
REFERENCES................................................................................................................................8
1

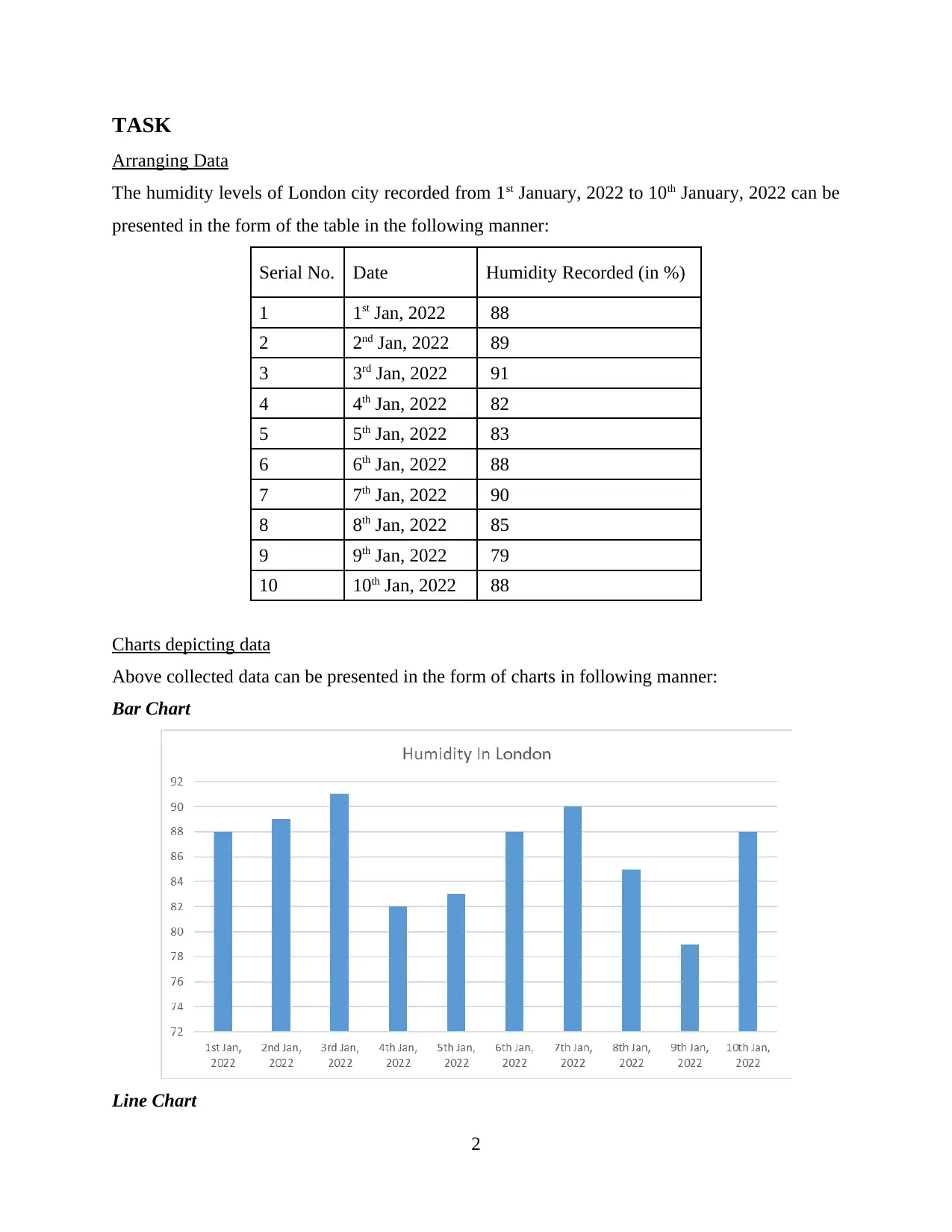
TASK
Arranging Data
The humidity levels of London city recorded from 1st January, 2022 to 10th January, 2022 can be
presented in the form of the table in the following manner:
Serial No. Date Humidity Recorded (in %)
1 1st Jan, 2022 88
2 2nd Jan, 2022 89
3 3rd Jan, 2022 91
4 4th Jan, 2022 82
5 5th Jan, 2022 83
6 6th Jan, 2022 88
7 7th Jan, 2022 90
8 8th Jan, 2022 85
9 9th Jan, 2022 79
10 10th Jan, 2022 88
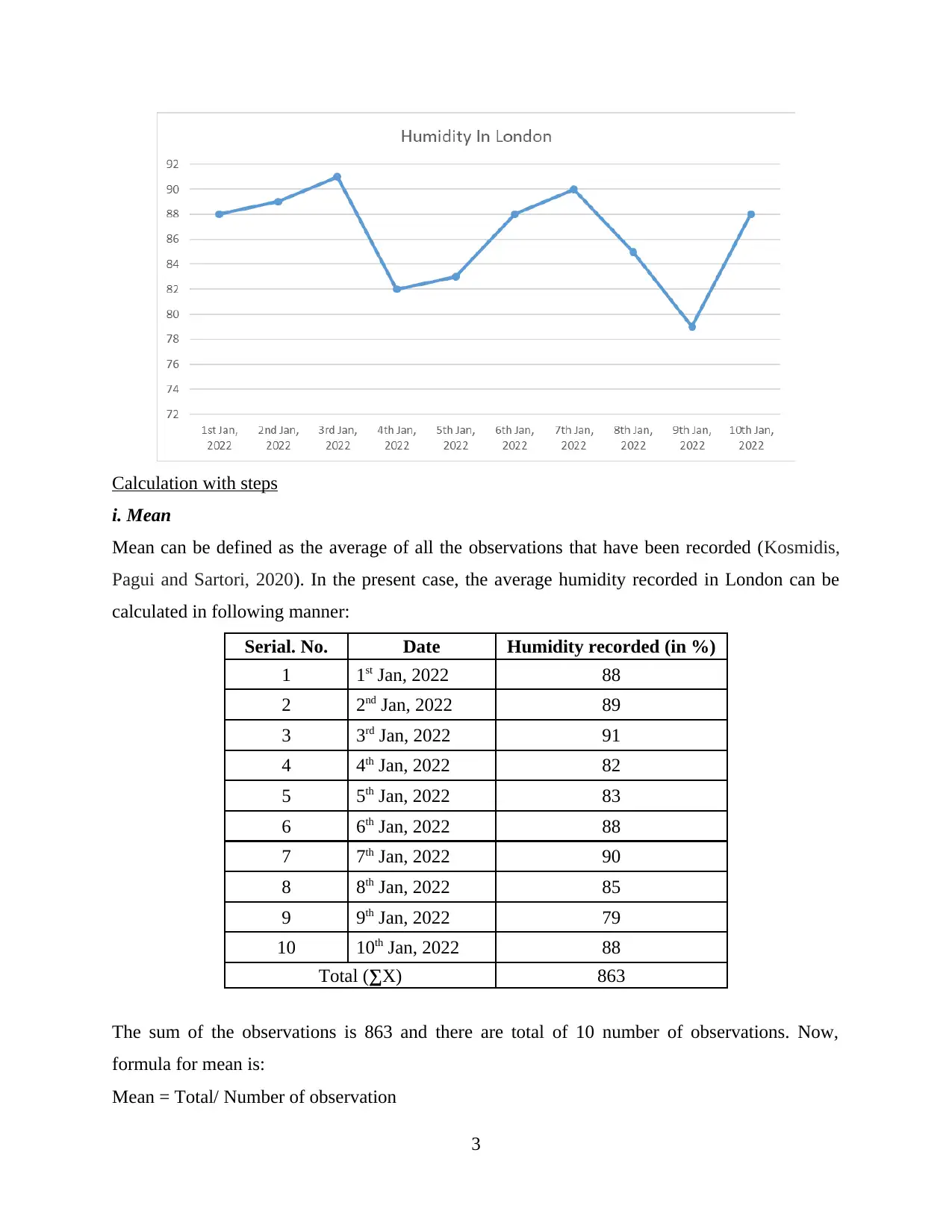
Charts depicting data
Above collected data can be presented in the form of charts in following manner:
Bar Chart
Line Chart
2

Calculation with steps
i. Mean
Mean can be defined as the average of all the observations that have been recorded (Kosmidis,
Pagui and Sartori, 2020). In the present case, the average humidity recorded in London can be
calculated in following manner:
Serial. No. Date Humidity recorded (in %)
1 1st Jan, 2022 88
2 2nd Jan, 2022 89
3 3rd Jan, 2022 91
4 4th Jan, 2022 82
5 5th Jan, 2022 83
6 6th Jan, 2022 88
7 7th Jan, 2022 90
8 8th Jan, 2022 85
9 9th Jan, 2022 79
10 10th Jan, 2022 88
Total (∑X) 863
The sum of the observations is 863 and there are total of 10 number of observations. Now,
formula for mean is:
Mean = Total/ Number of observation
3

i.e., 863/ 10 = 86.3%
On an average, the humidity level of London can have said to be at 86.3% from 1st January to
10th January, 2022.
ii. Median
Median can be defined as the middle most value that has been recorded amongst a set of
observations (Mishra and et.al., 2019). It lies exactly in between of both the ends. Median can be
calculated in following manner:
Step 1: Arranging the data in ascending order:
79, 82, 83, 85, 88, 88, 88, 89, 90, 91
Step 2: Application of formula (n + 1)/ 2,
Where, n = number of observations, i.e.,
Median position = (10 + 1)/ 2 = 5.5th observation is the median value. This means that the
median value lies between 5th and 6th observation respectively.
Now median = 5th observation + 6th observation/ 2, i.e.,
Here 88 lies on 5th as well as 6th position, i.e. 88 + 88 / 2 = 88. Hence the middle value of the
humidity recorded of London is 88%.
iii. Mode
Mode is the most frequent value that has been recorded in a set of observations (Kaur, P.,
Stoltzfus and Yellapu, 2018). Here, in the recorded set of observations, the highest number of
repetition in humidity levels is found to be at 88% which is recorded for 3 times in 10 days.
Hence, mode is 88%.
iv. Range
Range is basically difference of maximum and minimum values form a set of observation.
Range = Highest value – smallest value
Here, at present, 91% is highest humidity level and 79% is the lowest. Therefore,
Range = 91 – 79 i.e. 12.
It can be said that the range within which humidity levels have been recorded is very small at
only 5 units.
v. Standard Deviation
SD indicates the average deviation that occurs from the mean value for a recorded set of data. It
indicates how far values have extended at both the extremes from the average recorded value
4

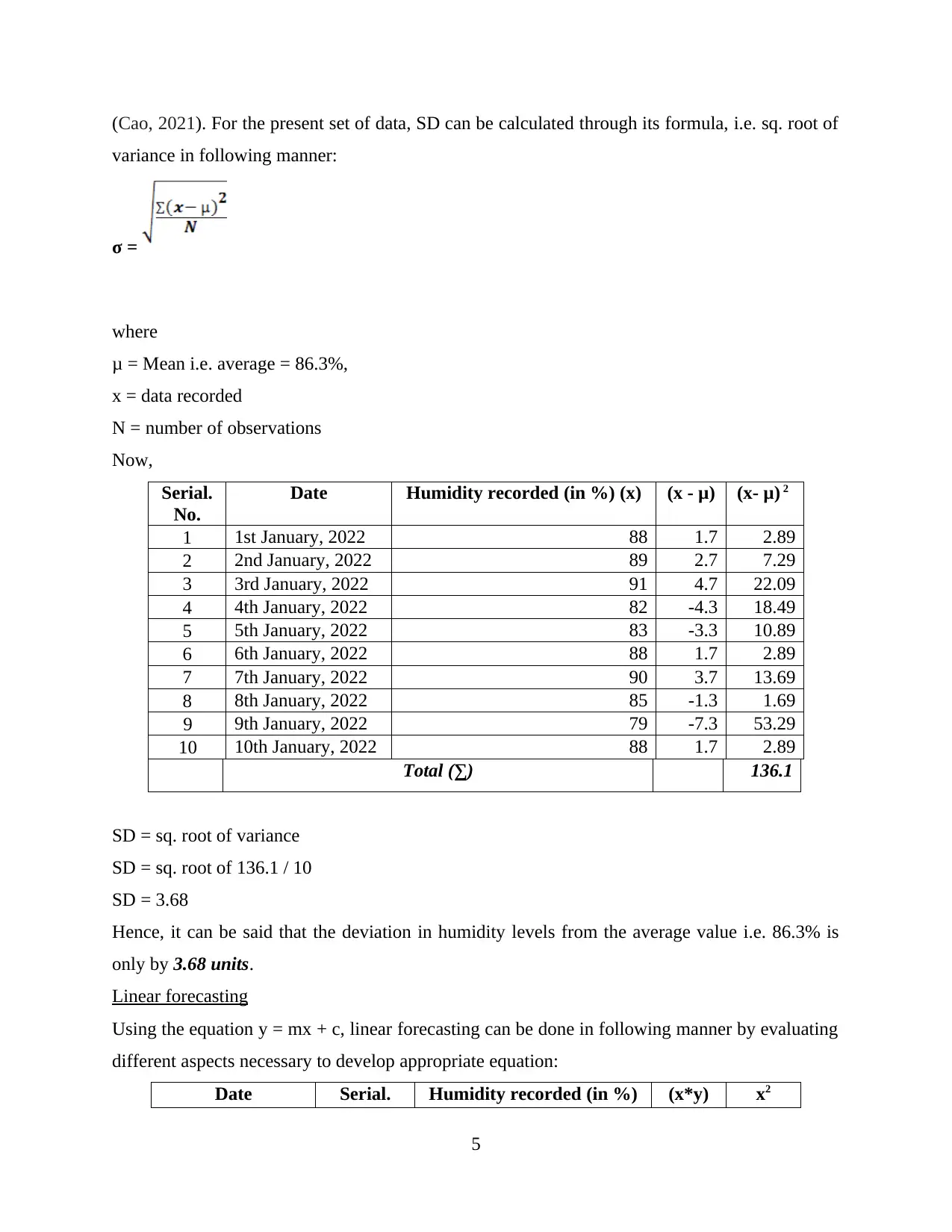
(Cao, 2021). For the present set of data, SD can be calculated through its formula, i.e. sq. root of
variance in following manner:
σ =
where
μ = Mean i.e. average = 86.3%,
x = data recorded
N = number of observations
Now,
Serial.
No.
Date Humidity recorded (in %) (x) (x - μ) (x- μ) 2
1 1st January, 2022 88 1.7 2.89
2 2nd January, 2022 89 2.7 7.29
3 3rd January, 2022 91 4.7 22.09
4 4th January, 2022 82 -4.3 18.49
5 5th January, 2022 83 -3.3 10.89
6 6th January, 2022 88 1.7 2.89
7 7th January, 2022 90 3.7 13.69
8 8th January, 2022 85 -1.3 1.69
9 9th January, 2022 79 -7.3 53.29
10 10th January, 2022 88 1.7 2.89
Total (∑) 136.1
SD = sq. root of variance
SD = sq. root of 136.1 / 10
SD = 3.68
Hence, it can be said that the deviation in humidity levels from the average value i.e. 86.3% is
only by 3.68 units.
Linear forecasting
Using the equation y = mx + c, linear forecasting can be done in following manner by evaluating
different aspects necessary to develop appropriate equation:
Date Serial. Humidity recorded (in %) (x*y) x2
5

No. (x) (y)
1st January, 2022 1 88 88 1
2nd January, 2022 2 89 178 4
3rd January, 2022 3 91 273 9
4th January, 2022 4 82 328 16
5th January, 2022 5 83 415 25
6th January, 2022 6 88 528 36
7th January, 2022 7 90 630 49
8th January, 2022 8 85 680 64
9th January, 2022 9 79 711 81
10th January, 2022 10 88 880 100
Sum 55 863 4711 385
Now,
i. Calculating m
m =
m = [(10*4711) – (55*863)]/ [(10*385) – (55) 2]
m = [47110 - 47465]/ [3850 - 3025]
m = -355/ 825
m = -0.43
ii. Calculating c
c =
c = [863 – (-0.43 * 55)]/ 10
c = [863 – (-54.57)]/ 10
c = 91.75
iii. Forecasting humidity for 11th and 13th day respectively
Using equation y = mx + c and inputting the calculated value of m and c, forecasted humidity
percentage can be identified as:
6

Y = (-0.43) x + 91.75
Forecasted Humidity level for 11th day =
Y = (-0.43) * 11 + 91.75
Y = 87.02%
Forecasted Humidity level for 13th day =
Y = (-0.43) * 13 + 91.75
Y = 86.16%
Hence, humidity levels for 11th and 13th day, as forecasted, will be 87.02% and 86.16%
respectively.
7

REFERENCES
Books and Journal
Cao, W., 2021. Discussion on Mean, Median, Mode and its Validity and Table Number. Journal
of Contemporary Educational Research. 5(3).
Kaur, P., Stoltzfus, J. and Yellapu, V., 2018. Descriptive statistics. International Journal of
Academic Medicine. 4(1). p.60.
Kosmidis, I., Pagui, E.C.K. and Sartori, N., 2020. Mean and median bias reduction in
generalized linear models. Statistics and Computing. 30(1). pp.43-59.
Mishra, P., and et.al., 2019. Descriptive statistics and normality tests for statistical data. Annals
of cardiac anaesthesia. 22(1). p.67.
8