Report on Numeracy and Data Analysis of Humidity Levels in Wales

This report presents a data analysis of humidity levels in Wales, utilizing various statistical methods and a linear forecasting model. The analysis includes arranging humidity data collected over ten days into a table and generating column and line charts to visualize the data. Key statistical measures such as mean, median, mode, range, and standard deviation are calculated with detailed step-by-step explanations. Furthermore, a linear forecasting model is applied to frame a regression equation, calculating the values of 'm' (slope) and 'c' (vertical intercept). Based on this model, the humidity levels for day 11 and day 13 are forecasted. The report concludes by summarizing the findings of the data evaluation and the application of the linear forecasting model.

Numeracy and Data
Analysis - Individual
Assessment

Contents
INTRODUCTION...........................................................................................................................3
MAIN BODY..................................................................................................................................3
1. Arrange the data in the table format........................................................................................3
2. Prepare the charts of the above table.......................................................................................3
3. Calculate the following by explaining all the steps of calculation..........................................4
4. Using the linear forecasting model frame the regression equation and calculate the value of
m and c.........................................................................................................................................7
a) Calculate the value of m by writing down the steps of calculation.........................................7
b) Calculate the value of c by writing down the steps of computation........................................8
c) Calculate the value of m and c on day 11 and 13....................................................................8
CONCLUSION................................................................................................................................9
REFERENCES..............................................................................................................................10

INTRODUCTION
Data analysis is done on the collection of the certain information (Cheung, Dulay and
McBride, 2020). The data in the report is collected of the city Wales which is in the United
States and the descriptive analysis will be performed of the data. Further, the regression equation
will be formed and the forecast calculation of 2 days will be made on the basis of the equation.
MAIN BODY
1. Arrange the data in the table format.
Humidity Data
Day (x) Humidity (y)
1 80
2 78
3 89
4 97
5 83
6 87
7 92
8 75
9 66
10 79
2. Prepare the charts of the above table.
1 2 3 4 5 6 7 8 9 10
0
20
40
60
80
100
120
Humidity level

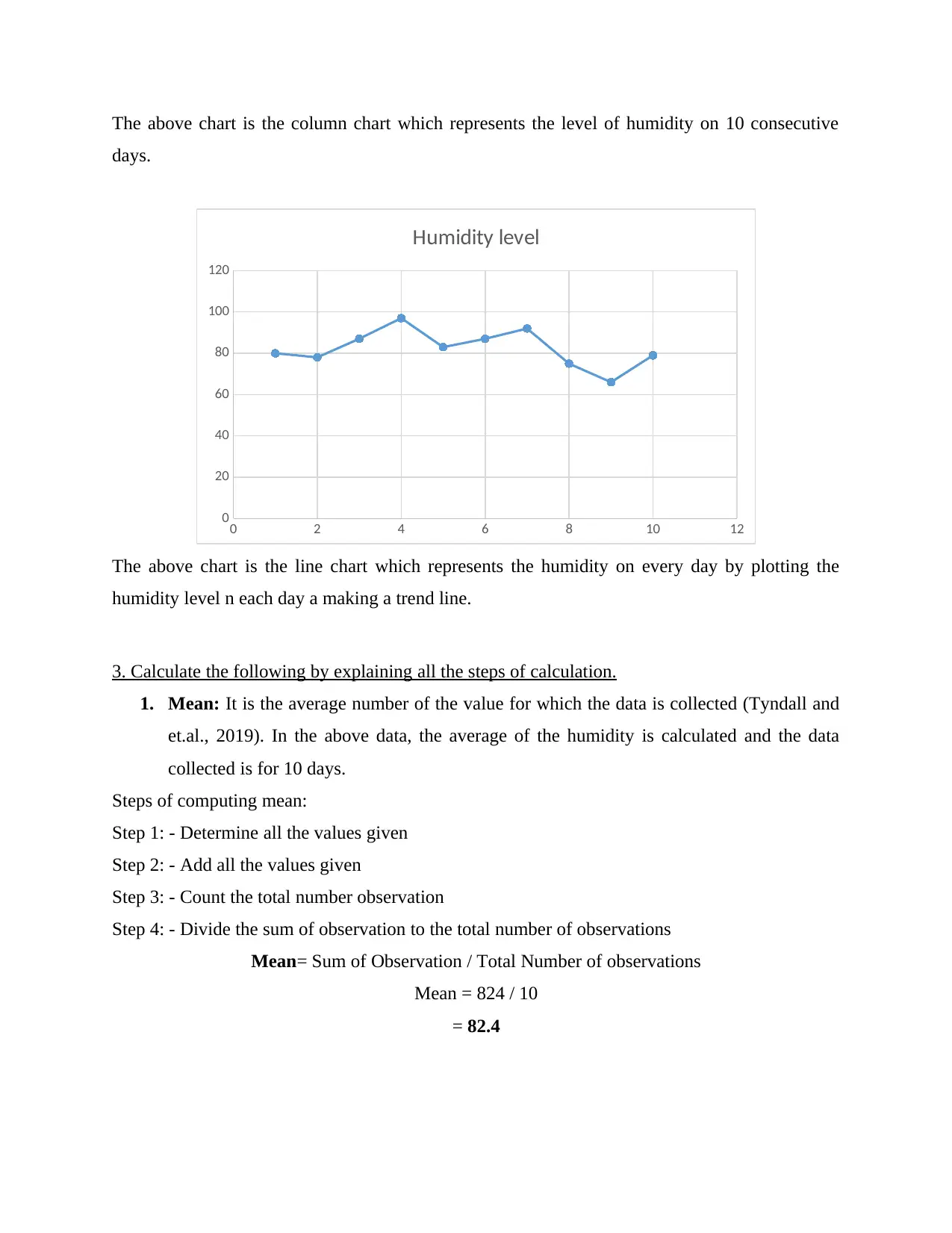
The above chart is the column chart which represents the level of humidity on 10 consecutive
days.
0 2 4 6 8 10 12
0
20
40
60
80
100
120
Humidity level
The above chart is the line chart which represents the humidity on every day by plotting the
humidity level n each day a making a trend line.
3. Calculate the following by explaining all the steps of calculation.
1. Mean: It is the average number of the value for which the data is collected (Tyndall and
et.al., 2019). In the above data, the average of the humidity is calculated and the data
collected is for 10 days.
Steps of computing mean:
Step 1: - Determine all the values given
Step 2: - Add all the values given
Step 3: - Count the total number observation
Step 4: - Divide the sum of observation to the total number of observations
Mean= Sum of Observation / Total Number of observations
Mean = 824 / 10
= 82.4

2. Median: It is the value which is derived from the arrangement of the data is the
ascending order. It is the mid – value of the series and is termed as median.
Steps to calculate median:
Step 1: - First of all arrange the data in ascending order (smallest to largest number)
Step 2: - Then calculate the number of observations whether it is odd/even.
Step 3: - If it is Even, then the following formula should be used (N/2)
Step 4: - And if it is odd, then the following formula should be used ((N+1)/2)
Step 5: - The resulted outcome is the position of the median. Arrange the data first n the
ascending order:
Median= (N + 1 / 2)
= (10 + 1) / 2
= 11 / 2 = 5.5
80, 78, 87, 97, 83, 87, 92, 75, 66, 79
66, 75, 78, 79, 80, 83, 87, 87, 92, 97
So the median in this data is (80 + 83) / 2 = 81.5
3. Mode: It is the value which occurs the most number of times in the data (Tang and et.al.,
2020).
Steps to calculate Mode: -
Step 1: - Collect and organise the data given.
Step 2: - Find out the distinct values.
Step 3: - Count the Frequency of occurrence of the data.
Step 4: - Most occurred value is the Mode.
80, 78, 87, 97, 83, 87, 92, 75, 66, 79
It can be observed from the have data that the value which has been repeated most number
of times is 87. It has been repeated 2 times.
4. Range:
Steps to calculate Range: -
Step 1: - Arrange all the data available.
Step 2: - Then identify the highest and the lowest value.

Step 3: - Subtract the lowest value from the highest.
Step 4: - The value we get after the third step is the Range.
Range= Maximum Value – Minimum value
Range = 97 – 66
= 31
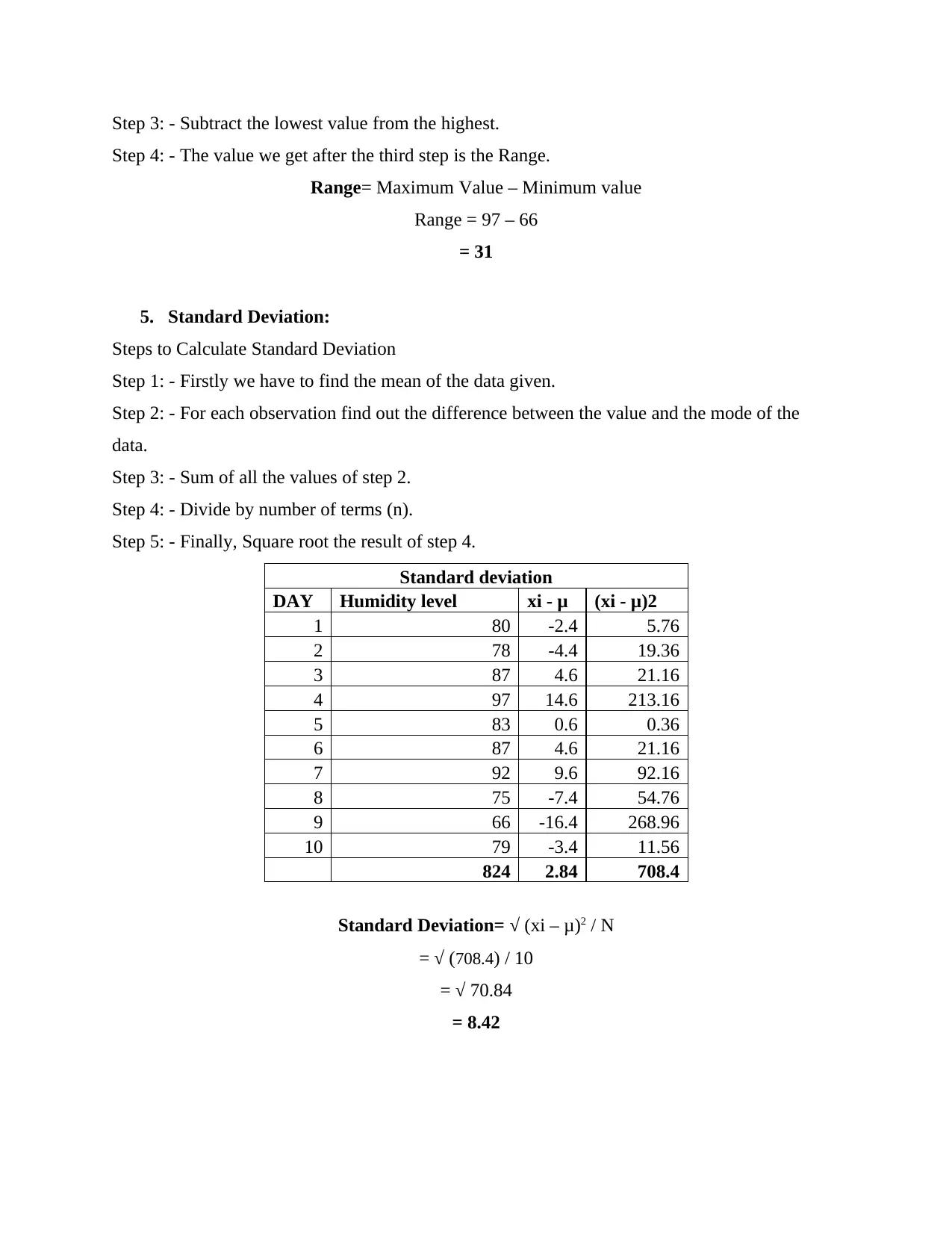
5. Standard Deviation:
Steps to Calculate Standard Deviation
Step 1: - Firstly we have to find the mean of the data given.
Step 2: - For each observation find out the difference between the value and the mode of the
data.
Step 3: - Sum of all the values of step 2.
Step 4: - Divide by number of terms (n).
Step 5: - Finally, Square root the result of step 4.
Standard deviation
DAY Humidity level xi - μ (xi - μ)2
1 80 -2.4 5.76
2 78 -4.4 19.36
3 87 4.6 21.16
4 97 14.6 213.16
5 83 0.6 0.36
6 87 4.6 21.16
7 92 9.6 92.16
8 75 -7.4 54.76
9 66 -16.4 268.96
10 79 -3.4 11.56
824 2.84 708.4
Standard Deviation= √ (xi – μ)2 / N
= √ (708.4) / 10
= √ 70.84
= 8.42

4. Using the linear forecasting model frame the regression equation and calculate the value of m
and c.
Linear Forecasting Model: - It predicts ' future values' based on the 'past values' in a
linear equation. (Abuya and et.al., 2018)
y = mx + c
where, 'y' is the dependent variable
'mx' is the independent variable
'c' is the constant
a) Calculate the value of m by writing down the steps of calculation.
Steps of Calculating m is:
1. Multiply both the variables X and Y which are named as days and humidity.
2. Doing the sum of the above calculation.
3. Sum of the x variable and y factor individually.
4. Then multiply both the factors.
5. Calculate ( x)⅀ 2 at the end put the values in the formula.
6. The resultant value is the value of 'm'.
Linear forecasting model
DAY Humidity level xy x^2
1 80 80 1
2 78 156 4
3 87 261 9
4 97 388 16
5 83 415 25
6 87 522 36
7 92 644 49
8 75 600 64
9 66 594 81
10 79 790 100
55 824 4450 385
m = 10 * 4450 – 4450 / 10* 385 – 385

= 44500 – 4450 / 3850 – 385
= 40050 / 3465
= 11.55
The above value of m denotes the slope of the line which is 11.55.
b) Calculate the value of c by writing down the steps of computation.
Steps of calculating c:
1. First of all, calculate the sum of 'y' variable.
2. Then calculate the sum of 'x' variable.
3. Finally divide it with the sum of 'N'.
4. The value derived from Step 3 is the value of 'c'.
c = 824 – 11.55 * 55 / 10
= 824 – 635.25 / 10
= 188.75 / 10
= 18.875
The above value computed of c represents the vertical intercept of the regression equation.
c) Calculate the value of m and c on day 11 and 13.
Humidity on Day 11: -
m = 11.55, c = 18.875, x = 11,
y = mx + c
y = (11.55 * 11) + 18.875
y = 127.05 + 18.875
y = 145.925
Humidity on Day 13: -
m = 11.55, c = 18.875, x =13
y = mx+ c
y = (11.55 * 13) + 18.875
y = 150.15 + 18.875
y = 169.025

CONCLUSION
From the above data it can be concluded that the data of the humidity level of Wales was
evaluated on the basis of Mean, range, standard deviation, mode and median. Further the
regression equation was formed using the linear forecasting model.

REFERENCES
Books and Journals
Abuya, B.A. And et.al., 2018. Mothers’ education and girls’ Achievement in Kibera: The link with self-
efficacy. SAGE Open. 8(1). p.2158244018765608.
Cheung, S.K., Dulay, K.M. and McBride, C., 2020. Parents’ characteristics, the home environment, and
children’s numeracy skills: How are they related in low-to middle-income families in the
Philippines?. Journal of experimental child psychology. 192. p.104780.
Tang, X. and et.al., 2020. Latent feature extraction for process data via multidimensional
scaling. Psychometrika. 85(2). pp.378-397.
Tyndall, V. and et.al., 2019. Marked improvement in HbA 1c following commencement of flash glucose
monitoring in people with type 1 diabetes. Diabetologia. 62(8). pp.1349-1356.