Numeracy and Data Analysis: Computation and Explanation of Data Analysis on Temperature

This report focuses on data numeracy and its importance in evaluating and understanding accumulated data. It includes the computation and explanation of data analysis on temperature, including mean, median, mode, standard deviation, and range. The report also presents the information using two types of graphs and tables and computes the linear anticipating model to estimate future weather conditions.

Numeracy

Table of Contents
INTRODUCTION...........................................................................................................................3
MAIN BODY...................................................................................................................................3
1. Arrangement the information in suitable table format.......................................................3
2. Present the information using two types of graphs............................................................3
3. Computation and explanation of data analysis on Temperature........................................4
1. Arrangement the information in suitable table format.......................................................5
4. Calculation and definition of linear forecasting.................................................................6
CONCLUSION................................................................................................................................8
REFERENCES................................................................................................................................9

INTRODUCTION
Data numeracy is undertaken as the crucial method of statistics which aids business entities,
sector and governments for understandings as well as evaluating the accumulated with value
simple and faster. Additionally, this always represented into numerical or quantitative way. Into
the particular report, 10 random days of London city temperature level are accumulated.
Thereafter, fives data numeracy forms formulas are executed upon accumulated information
which mean, mode, standard deviation, median and range along with its stapes or meaning. In
addition to this, the particular report also highlights of the information into two several kinds f
graphs and tables. This in future computes the liner anticipating model in which they figure out
the value of ‘m’ as well as ‘c’ and then day 11 or 14 temperatures are anticipate.
MAIN BODY
1. Arrangement the information in suitable table format
Day
Wind
Speed
1 25
2 28
3 29
4 32
5 24
6 20
7 22
8 25
9 26
10 25
Total 256
2. Present the information using two types of graphs

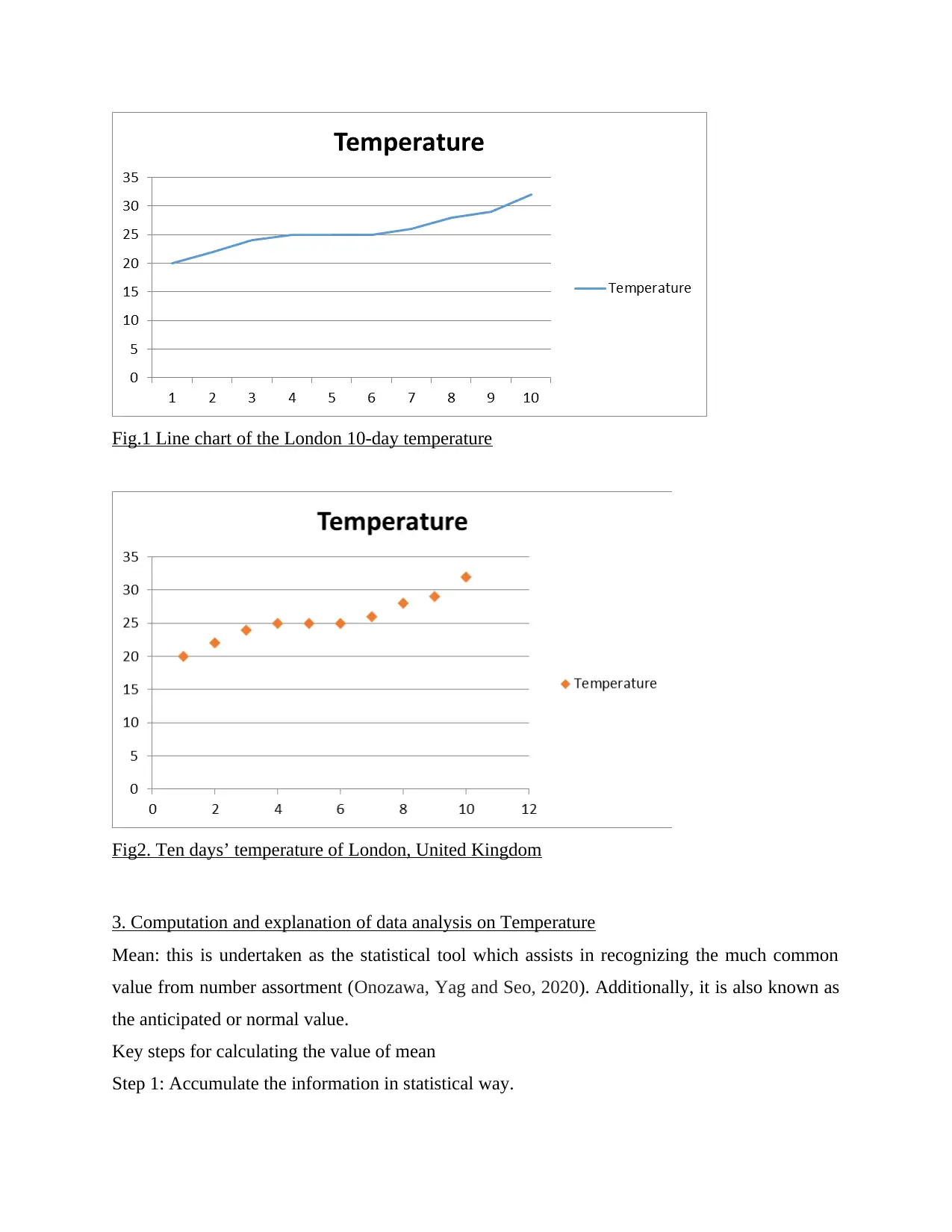
Fig.1 Line chart of the London 10-day temperature
Fig2. Ten days’ temperature of London, United Kingdom
3. Computation and explanation of data analysis on Temperature
Mean: this is undertaken as the statistical tool which assists in recognizing the much common
value from number assortment (Onozawa, Yag and Seo, 2020). Additionally, it is also known as
the anticipated or normal value.
Key steps for calculating the value of mean
Step 1: Accumulate the information in statistical way.

Step 2: Organize the information.
Step 3: Add the importance of data collection
Step 4: At the end, divide the above step outcomes in number of information into provide table.
Subsequent LY below London temperature mean computations are provided
Mean = Aggregate of all worth / Number of value
x = 256 / 10
Mean = 25.6
1. Arrangement the information in suitable table format
I. Median: The substance which present in the middle point when standards are set in an
ascending order is referred to as median (Tout, 2020).
Phases for calculation of median
Phase 1: Firstly the frequency of the information available is identified to get quantitative results
Phase 2: Organization or arrangement of the data points in an increasing or decreasing manner.
Phase 3: This is an important phase which involves determination of data at the middle.
Phase 4: In this phase data is counted weather it is even or odd.
Phase 5: The last phase involved application of the formula to get the answer.
The application of above phases is completed below to devise median of London heat conditions
Data set = 25, 28, 29, 32, 24, 20, 22, 25, 26, 25
Ascending order = 20, 22, 24, 25, 25, 25, 26, 28, 29, 32
Median = (Number of term + 1) / 2
= (10+1) / 2
Median = 5.5
Here it is devised that the numerical value between the fifth and sixth data points in the data
group is the median.
Aggregate for the numerical values for both is provided below
Median = (25+25) / 2
Median = 25
II. Mode: The numerical value whose frequency is highest is defined as the mode of a given
data set (Mendez-Carbaj, Jefferson and Stierholz, 2019).
Phases which can be applied to identifying mode
Phase 1: Arrangement of the information in an increasing or decreasing fashion.

Phase 2: Determination of the numerical value which occurs the most
Phase 3: The value which is identified in the second phase is considered mode of the data set
In case of the data set of London heat conditions data set:
Rising direction = 20, 22, 24, 25, 25, 25, 26, 28, 29, 32
Mode = 25
III. Standard Deviation: The statistical value shows the dispersion of data in relation to the
mean (Hwang, 2020).
Formulation for determining Standard deviation:
The calculation for standard deviation of heat conditions data in London is provided below:
SD of London heat conditions data = √∑ (xi – μ) 2 / N
= √ (106.4 / 10)
SD of London heat conditions data =3.26
IV. Range: In simple terms it refers to the difference calculated by subtracted the highest
valued numerical data from lowest value numerical data in a data set (Heilmann, 2020).
Range = uppermost quantity of data group – lowermost numerical value of data group
The range in case of London heat data set is devised below:
Rising direction of data = 20, 22, 24, 25, 25, 25, 26, 28, 29, 32
Range of London heat conditions data = Greatest valued number– Least valued number
= 32 – 20
Range = 12
4. Calculation and definition of linear forecasting
It is a statistical instrument which is applied for estimating upcoming standards on the
basis of historical standards (Estrada‐Mejia and et. al., 2020). In case of weather estimation

linear forecasting is important as it helps use existing and past weather and temperature data to
estimate future weather conditions.
The given phases can be applied for calculation of forthcoming data on the basis of existing data:
Phase 1: Observation and collection of relevant information.
Phase 2: Completion of data analysis from the foundational stage.
Phase 3: Usage of the formulation of linear forecasting to get accurate results.
Procedure to compute linear Forecasting
y= mx + c
The above stated formulation “y” depicts the autonomous aspect, “mx” is for the dtermination of
dependent aspect and “c” signifies persistent aspect.
Phases to identify the numerical value of “m”
Phase 1: Totaling the complete quantity of “x” and “y” variables.
Phase 2: Multiplication of 'x' and 'y' variables and computation of ∑xy.
Phase 3: After this the square root x and y aspect.
Phase 4: After this each of the values is used in the formulation of the linear forecasting model.
M= ((10*1374) – (55*256)) / ((10*385) – (55)2)
M= (13740-14080) / (3850 – 3025)
M = -340 / 825
M = -0.412
Phases for determining the valuation of 'c' variable.
Phase 1: Addition of complete value of 'y' variable.
Phase 2: Consideration of the valuation of 'm'.
Phase 3: Multiplication of quantity of 'x' with quantity of 'm'
Phase 4: Subtraction of the y quantity from Phase 3
Phase 5: After this the result of Phase 4 is divided by 'n'
C = (256- (-0.412 * 55)

C = (256 + 22.66)
C = 278.66
Day 11 heat conditions of London:
M = -0.412, x= 11 and c = 278.66
Y = mx+c
Y = (-0.412*11)+ 278.66
Y = -4.532+278.66
Y = 274.128
Day 14 heat conditions:
M = -0.412, x= 14 and c = 278.66
Y = mx+c
Y = (-0.412*14) + 278.66
Y = -5.768+278.66
Y = 272.892
CONCLUSION
From the above discussion it is determined that information numeracy is an advantageous
and inexpensive way of building a complicated database. The database developed from the above
information is devised on the3 basis of heat conditions of London from ten days. There are
various formulations and statistical information which can be used for determining useful
outcome such as standard deviation or mean. Finally the determination of the numerical value of
“m” and “c” in the linear forecasting model depicts the result of eleventh and fourteenths days of
predicted weather conditions.

REFERENCES
Books and Journals
Estrada‐Mejia and et. al., 2020. Schooling, numeracy, and wealth accumulation: A study
involving an agrarian population. Journal of Consumer Affairs, 54(2). pp.648-674.
Heilmann, L., 2020. Health and numeracy: The role of numeracy skills in health satisfaction and
health-related behaviour. ZDM, 52(3). pp.407-418.
Hwang, S., 2020. Examining the effect of students’ early numeracy activities at home on later
mathematics achievement via early numSeracy competencies and self-efficacy
beliefs. International Electronic Journal of Elementary Education, 13(1). pp.47-56.
Mendez-Carbajo, D., Jefferson, C. O. and Stierholz, K. L., 2019. Keeping It Real: Information
Literacy, Numeracy, and Economic Data. Numeracy: Advancing Education in
Quantitative Literacy, 12(2).
Tout, D., 2020. Evolution of adult numeracy from quantitative literacy to numeracy: Lessons
learned from international assessments. International Review of Education, 66(2).
pp.183-209.
Onozawa, M., Yagi, A. and Seo, T., 2020. New Test Statistics for One and Two Mean Vectors
with Two-step Monotone Missing Data. International Journal of Statistics and
Probability, 9(6). pp.1-56.