Numeracy and Data Analysis: Calculation of Mean, Median, Range, Standard Deviation and Linear Forecasting Model

This report covers the calculation of Mean, Median, Range, Standard Deviation and Linear Forecasting Model with the help of temperature data of Belfast city of UK for ten consecutive days. It also includes the presentation of data through charts and the role of data analysis in decision-making.

NUMERACY AND
DATA ANALYSIS

Table of Contents
INTRODUCTION...........................................................................................................................3
MAIN BODY...................................................................................................................................3
Data arranged in a Table Format.................................................................................................3
Present the data with using two charts........................................................................................4
Calculate the value of Mean, Median, Range and Standard deviation.......................................5
Linear Forecasting Model...........................................................................................................8
CONCLUSION .............................................................................................................................11
REFERENCES..............................................................................................................................12

INTRODUCTION
Data analysis is a method of transforming and inspecting the data with the objective of
finding useful information (Castañeda and et.al, 2020). It plays an important role in decision-
making. In this report, data is collected for ten consecutive days and presented the information
through various charts and calculated mean, mode, median and standard deviation. Using linear
forecasting model, calculate the value of “m” and “c”.
MAIN BODY
Data are collected for taking decision making. It is collected from different sources and used for
the purpose of analysis. Data is arranged in specific form, that is called information. When data
are processed in such manner that depicts some useful information out of it. Interpretation and
presentation are two method for data analysis. The data is divided into two parts. Nominal data
and ordinal data are type of qualitative data. Nominal data is also called nominal scale. Under
this method data are analysed by grouping method. Discrete data and continuous data are part of
quantitative data. It gives the information about the quantities of thing.
Data arranged in a Table Format
The below data is presented the temperature of Belfast city of UK for ten consecutive days which
are arranged in a table format as follow-
Days Temperature in degree (Celsius)
Day1 15
Day2 14
Day3 11
Day4 12
Day5 11
Day6 13
Day7 13
Day8 13
Day9 13

Day10 12
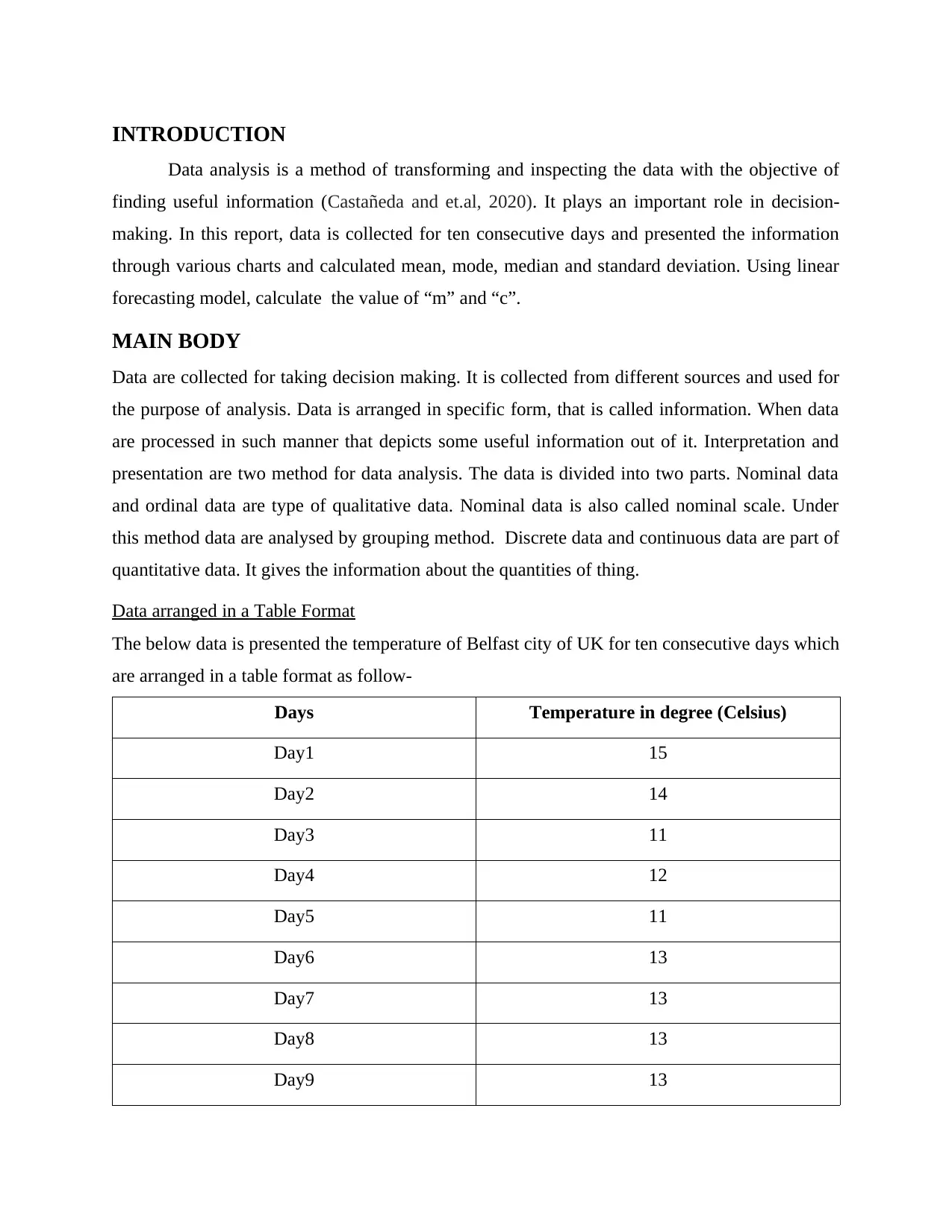
Present the data with using two charts
Column Chart- In this chart the data is represented in rectangle. Column chart is also
known as vertical bar charts. When the data has small number then uses of column chart so that
compare the value of each category (Goffin, and Ansari, 2019).
In the above chart, the temperature of Belfast city of UK for ten days data are
represented. Through this chart it can be said the temperature of 1st day was very high and the
temperature of 3rd and 5th day were lowest. The average temperature of Belfast was 12.7 degree
Celsius.
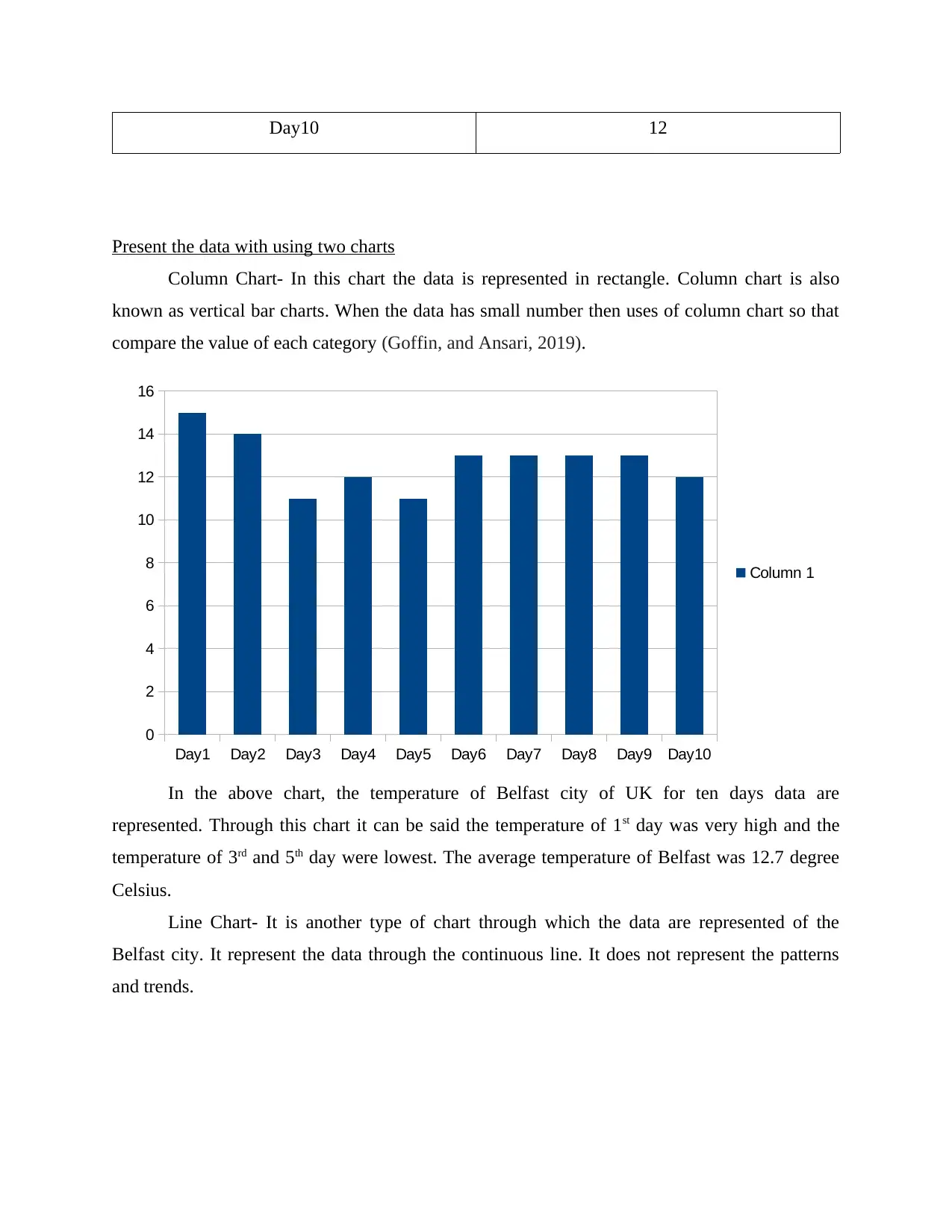
Line Chart- It is another type of chart through which the data are represented of the
Belfast city. It represent the data through the continuous line. It does not represent the patterns
and trends.
Day1 Day2 Day3 Day4 Day5 Day6 Day7 Day8 Day9 Day10
0
2
4
6
8
10
12
14
16
Column 1

Using line chart temperature of ten days are represented by line. It is very simple chart so that
people can easily understand it.
Calculate the value of Mean, Median, Range and Standard deviation.
Mean- It is the average of a data set. It requires adding all the numbers and dividing the
total number. There are different methods to calculate mean such as weighted average method,
standard deviation method and geometric mean (Pearce and et.al, 2018). On the basis of above
data the mean is calculated as follow-
Mean = ΣX / N
ΣX = (15+14+11+12+11+13+13+13+13+12)
ΣX = 127
Mean = 127/10
Mean = 12.7
Median- It is the middle of the set of numbers. It helps to identify a single data
through large data group. To calculate median firstly numbers are to arranged in
ascending to descending order. If the given data set is odd then median is most middle
value and given data set is even number then the average of two values selected as
middle value will be the median.
To calculate median firstly arranged all the values from least to highest.
Day1 Day2 Day3 Day4 Day5 Day6 Day7 Day8 Day9 Day10
0
2
4
6
8
10
12
14
16
Column 1

Days Temperature in degree (Celsius)
Day1 15
Day2 14
Day3 11
Day4 12
Day5 11
Day6 13
Day7 13
Day8 13
Day9 13
Day10 12
If n is even number then median is calculated as follow-
Median = ((n / 2)th + ( n / 2)+1th ) / 2
where n = number of terms
median = ((10/2)th +(10/2)+1th)/2
=(5+6)th term / 2
= (11+ 13) / 2
= 24 / 2
= 12
The median of given data is 12.
Mode- The value in the given data set which appears most of the time. It is very
easy to calculate it.
The mode of the given data the temperature of day-1 has the highest freqency.
The mode is 15 of the (day-1).
Range- It is difference between the highest and lowest value. To calculate range
firstly the data is arranged in ascending to descending order.
R = H - L

where R = Range
H = Highest value
L = Lowest value
Range = 15 – 11
Range = 4
The range of the temperature is 4
Standard Deviation- It measures the amount of variation or dispersion of a set of values.
It is mostly represent in mathematical texts (Shiyanbola and et.al, 2018). To calculate
standard deviation the following steps are to be followed.
Days Temperature (X – X bar) (X – X bar)2
Day1 15 15- 12.7= 2.3 5.29
Day2 14 14- 12.7 = 1.3 1.69
Day3 11 11- 12.7 = -1.7 2.89
Day4 12 12- 12.7= -0.7 0.49
Day5 11 11- 12.7= -1.7 2.89
Day6 13 13-12.7= 0.3 0.09
Day7 13 13-12.7= 0.3 0.09
Day8 13 13- 12.7= 0.3 0.09
Day9 13 13- 12.7 = 0.3 0.09
Day10 12 12- 12.7= -0.7 0.49
Total 165 14.1
The mean (x bar) of the above data is 12.7, which is calculated in above.
The Standard deviation of the given data set is as follow-

where s= sample standard deviation
n= total number of sample elements
x bar= mean
Standard deviation= square root of 14.1 / 10
S.D.= square root of 1.41
S.D. = 1.1874
The S.D. Of the temperature is 1.1874.
Linear Forecasting Model
It is statistical tool which helps to find future value on the basis of past data (Yang
and et.al, 2020).
The linear forecasting model is y = mx + b
where m represents the rate of change
x represent the input value
y represent the output value
b represent the constant value
Days Temperature xy x2
Day1 15 15 1
Day2 14 28 4
Day3 11 33 9
Day4 12 48 16
Day5 11 55 25

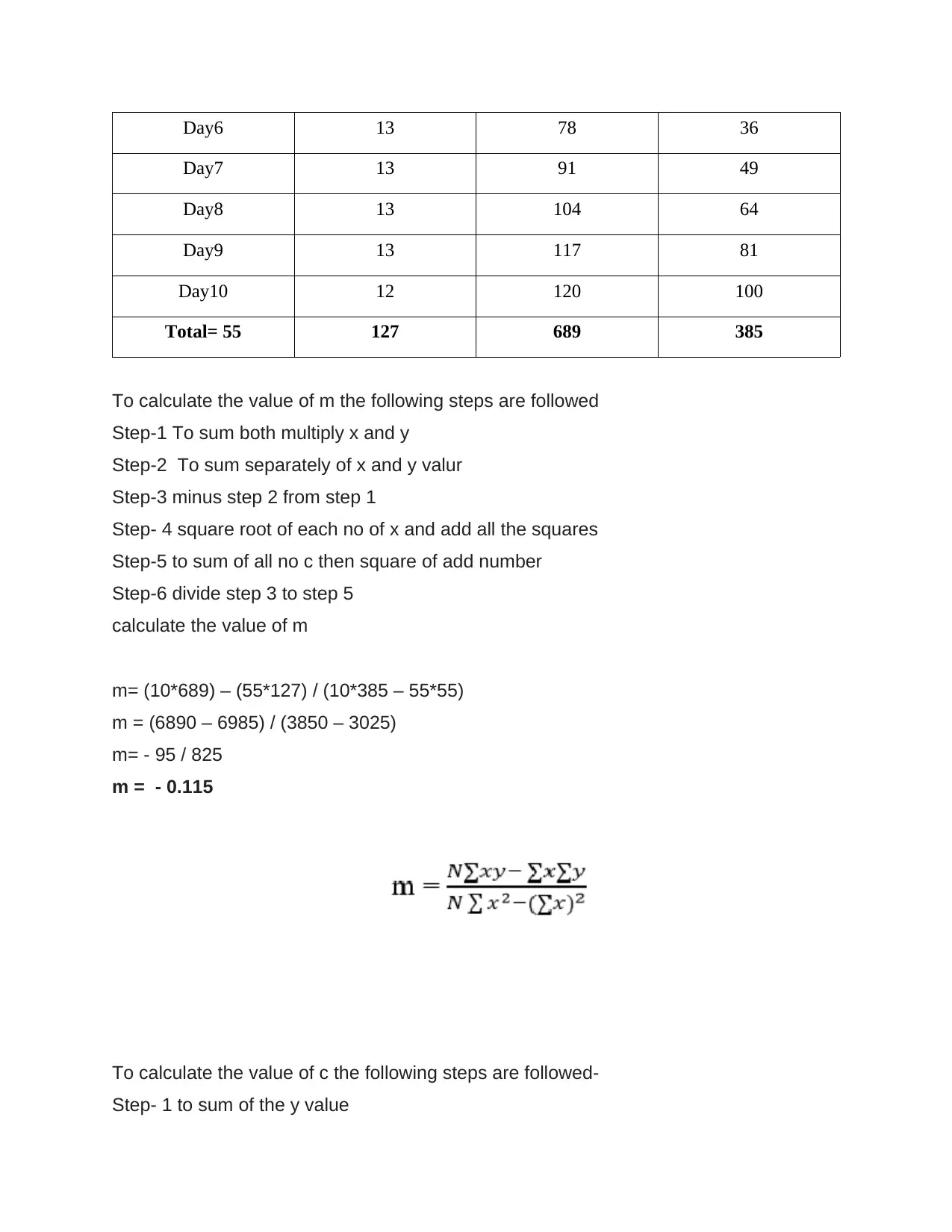
Day6 13 78 36
Day7 13 91 49
Day8 13 104 64
Day9 13 117 81
Day10 12 120 100
Total= 55 127 689 385
To calculate the value of m the following steps are followed
Step-1 To sum both multiply x and y
Step-2 To sum separately of x and y valur
Step-3 minus step 2 from step 1
Step- 4 square root of each no of x and add all the squares
Step-5 to sum of all no c then square of add number
Step-6 divide step 3 to step 5
calculate the value of m
m= (10*689) – (55*127) / (10*385 – 55*55)
m = (6890 – 6985) / (3850 – 3025)
m= - 95 / 825
m = - 0.115
To calculate the value of c the following steps are followed-
Step- 1 to sum of the y value

Step- 2 opt out the value of y
Step- 3 to sum of x and multiply with the value of m
Step- 4 subtract the sum of mx from the sum of fy
then c= (127- ( - 0.115*55))/10
c= (127-(- 6.325))/10
c= (127+6.325)/10
c= 133.325/10
c= 13.33
Temperature on 11th day-
where m= -0.115, c= 13.33 x= 11
y= mx+ c
= -0.115*11+13.33
= -1.265+13.33
= 12.065
The temperature of 11th day is 12.065 degree Celsius.
Temperature on 14th day-
where m= -0.115, c= 13.33 x= 14
y= mx+ c
= -0.115*14+13.33
= -1.61+13.33
= 11.72
The temperature of 14th day is 11.72 degree Celsius.

CONCLUSION
In the above report the calculations are performed to calculate mean, mode, median, standard
deviation and range of the data set of temperature in Belfast the city of U.K. For ten consecutive
days. With the help of forecasting model to calculated the value of m and c.

REFERENCES
Books and Journals
Castañeda and et.al, 2020. The role of numeracy and information load in the tourist decision‐
making process. Psychology & Marketing, 37(1), pp.27-40.
Goffin, C. and Ansari, D., 2019. How are symbols and nonsymbolic numerical magnitudes
related? Exploring bidirectional relationships in early numeracy. Mind, Brain, and
Education, 13(3), pp.143-156.
Pearce and et.al, 2018. The apples of academic performance: associations between dietary
patterns and academic performance in Australian children. Journal of School Health, 88(6),
pp.444-452.
Shiyanbola and et.al, 2018. The association of health literacy with illness perceptions, medication
beliefs, and medication adherence among individuals with type 2 diabetes. Research in
Social and Administrative Pharmacy, 14(9), pp.824-830.
Yang and et.al, 2020. Differential contributions of cognitive precursors to symbolic versus non-
symbolic numeracy in young Chinese children. Early Childhood Research Quarterly,53,
pp.208-216.