Ask a question from expert
Numerical Methods Assignment
11 Pages1301 Words192 Views
Added on 2020-04-29
Numerical Methods Assignment
Added on 2020-04-29
BookmarkShareRelated Documents
NUMERICAL METHODS

ContentsGraphical Method..................................................................................................................................2Bisection Method..................................................................................................................................3False Position Method...........................................................................................................................4Increment Search Method.....................................................................................................................5Simple Fixed point Iteration..................................................................................................................6Newton Raphson Method.....................................................................................................................6Secant Method......................................................................................................................................7Brents Method......................................................................................................................................7Multiple roots........................................................................................................................................8System of Non-linear Equation..............................................................................................................8

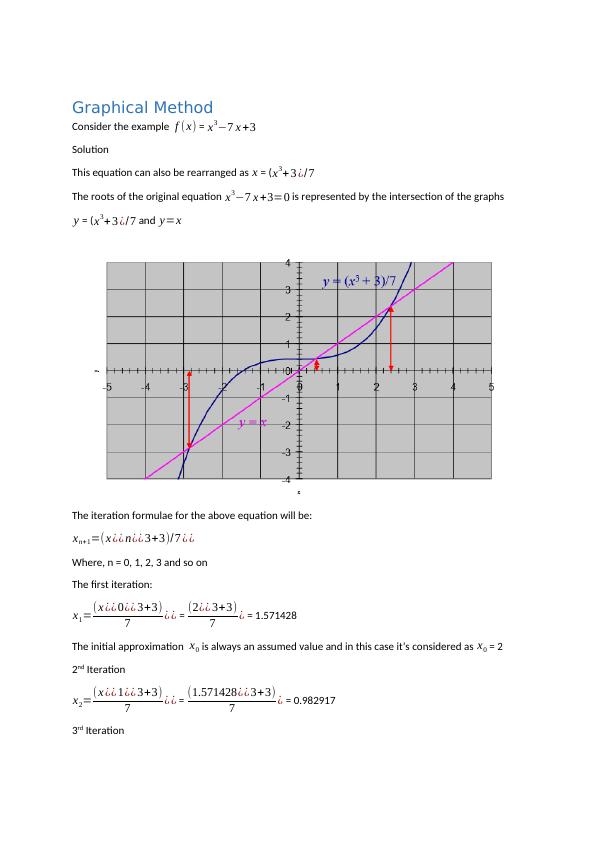
Graphical MethodConsider the example f(x) = x3−7x+3SolutionThis equation can also be rearranged as x = (x3+3¿/7The roots of the original equation x3−7x+3=0 is represented by the intersection of the graphs y = (x3+3¿/7 and y=xThe iteration formulae for the above equation will be:xn+1=(x¿¿n¿¿3+3)/7¿¿Where, n = 0, 1, 2, 3 and so onThe first iteration:x1=(x¿¿0¿¿3+3)7¿¿ = (2¿¿3+3)7¿ = 1.571428The initial approximation x0 is always an assumed value and in this case it’s considered as x0 = 22nd Iterationx2=(x¿¿1¿¿3+3)7¿¿ = (1.571428¿¿3+3)7¿ = 0.9829173rd Iteration
x3=(x¿¿2¿¿3+3)7¿¿ = (0.982917¿¿3+3)7¿ = 0.5642294th Iterationx4=(x¿¿3¿¿3+3)7¿¿ = (0.564229¿¿3+3)7¿ = 0.4542285th Iterationx5=(x¿¿4¿¿3+3)7¿¿ = (0.454228¿¿3+3)7¿ = 0.44195966th Iterationx6=(x¿¿5¿¿3+3)7¿¿ = (0.4419596¿¿3+3)7¿ = 0.440903Upon further iteration the root can be found out to be 0.441Bisection MethodConsider the equation f(x) = x2−3 starting on [1, 2]Solutionf(1) = 12−3 = -2 (negative value)f(2) = 22−3 = 1 (positive value)In this case, the starting point is already provided. But if it is not provided, we need to find 2 different approximation of x which yields a negative and positive value.1st Iterationx1 = (a+b)2 = (1+2)2 = 1.5 (Here, a and b are the starting points)Substituting, x1 in the equationf(1.5) = 1.52−3 = -0.75 This gives a negative value, which means we can neglect the previous negative value interval. The new interval becomes [1.5, 2]2nd Iterationx2 = (a+b)2 = (1.5+2)2 = 1.75 (Here, a and b are the starting points)Substituting, x1 in the equationf(1.75) = 1.752−3 = 0.0625

End of preview
Want to access all the pages? Upload your documents or become a member.
Related Documents
HNCB036 Applied Mathematics For Engineerslg...
|27
|566
|122
Mathematics Assignment | Estimation of Roots by Iterationlg...
|7
|1311
|108