Saint Louis University: Multiphase Flow Modeling Simulation

This project report provides a comprehensive analysis of multiphase flow modeling and simulation, focusing on the Euler-Euler approach and the phase field method. The study investigates two-phase flow in microchannels, comparing the phase field technique with traditional multiphase flow models. Simulations of air bubble experiments were conducted and validated against existing literature. The report discusses the limitations of Euler flow in simulating thin fluid films and explores the impact of wall bond on flow and pressure fields. Ultimately, the phase field technique is concluded to offer enhanced predictive accuracy in certain aspects compared to conventional multiphase flow models. The project was completed during the last semester of studies at Saint Louis University.

PROJECT REPORT CAREER EPISODES2
[Author Name(s), First M. Last, Omit Titles and Degrees]
[Institutional Affiliation(s)]

ABSTRACT
The paper presents a thorough report on the numerical of Euler-Euler multiphase flow modeling
and simulation project. Moreover, a similar report was additionally carried out against elective
quantity of liquid model dependent on the stage field strategy that was observed to be more
favorable in key angles, for example, the nonattendance of unphysical interfacial pressure
motions and the capacity to represent variations in the surface pressure power. Also these lines
foresee a few air pocket lengths under constant flow conditions while checking the material
science of homogeneous two-phase phase. Various air pocket experiments instruments were
simulated and analyzed against test discoveries in the literature. The simulation of a thin fluid
film at the tube wall was observed to be a confinement of generally works relating to Euler flow,
including the present(Simon, Foley, K. T., Carls, & Melkent 2005).
This was credited to be almost certain because of constrained dimensional and spatial goals as
well as erroneous contact point with elements instead of restrictions of the demonstrating
approach itself. The impact of wall bond was contemplated with regard to the flow and pressure
field in the tube. An approval of the model was accomplished through a great examination of the
numerically anticipated gas void portion and air pocket lengths with existing models and
connections. All in all, the phase field technique was finished up to have enhanced prescient
precision as for certain viewpoints when contrasted with traditional multiphase flow models.

INTRODUCTION
Micro scale techniques are rapidly infiltrating in new application territories because of their
demonstrated potential for process upgrade as well as gear estimate/volume decrease in various
building applications. At the point when ideally planned ,the intrinsic higher surface zone to
volume ratio of smaller scale frameworks gives considerable heat exchange upgrade while
keeping pressure drops at moderate dimensions. Two-phase flow in micro channels has been a
subject of heightened enthusiasm for the past couple of decades. Micro channel phase change
takes place where heat and mass exchangers are specifically required in applications which are
industrial in nature. The heat/mass exchange coefficients as high as 1,000,000 W/m2K are
expected to fulfill a portion of the high-transition cooling requirements of certain elite, complex
system. The flow highlights at the micro scale vary essentially from that of macro scale flow. On
the test front, there exists an immense sum of distributed works, beginning from the early
investigations of researchers for macro scale flow and that of scholars for flow at littler scales up
to works done in later occasions fundamentally concentrating on micro scale streams. Some
scholars as of late shared a far reaching audit of the test works relating to gas-fluid two-stage
streams in micro channels. They grouped the observed flow system into the surface pressure
ruled sort, including Euler also, turbulent flow; the transitional sort, including stir and Euler
flows; and the inactivity ruled sort, including diffused as well as and streamlined flow . In the
considered flow designs, Euler stream described by an exchanging fluid of small and gas
particles design was actually the prevailing examination intrigue, particularly for micro scale
high temperature and weight exchangers. It was as a result within recycling speed segments in
either phase which improves convective blending. At present, a few spreading models that were

present for mathematical generation of two-stage stream within micro channels, for example, the
dispersed power display and the continuum surface power (CSF) display among others. The last
has been generally connected to use of the volume of flow (VOF) as well as similar dimension
group strategies. The phase field strategy has a place with the class of diffuse interface methods.
Be that as it may, dissimilar to the CSF alongside disseminated power models, which depend on
surface strain powers, a stage section technique as in view of available power. The two stage
are regarded as blend within the superficial region as well as correlation along these lines there is
connection with a blending energy as given by Eq. 1.
…………………………….1
The lambda is a scalar variable alluded to as the phase field variable as described by scholars and
is considered as a ratio of phase. It takes two particular qualities in either phase and experiences
a fast smooth change in the interfacial region. This blending energy adds to the aggregate free
energy thickness of the framework, ftot (J/m3 ). Here, t is the blending energy thickness having
measurements of power (N) and f scales with the thickness of the interface (m). The sharp
interface plan is accomplished while the limit of J will be generally zero. This gives the
interfacial
…….2

As illustrated by scholars, the reliance of experimental precision on three client characterized
parameters: the interface width, the portability, and the component estimate, h, represented extra
stresses on record of the nonappearance of governance equations on their choice. It is noticed
that the component estimate, h, is considered here since the dimension of area goals that is
required is reliant on the client characterized thickness of the interface. To conquer these issues,
an equation, h ≤ lambda sign was proposed by, where h and lambda symbol are the component
estimate and interface thickness parameter separately. Further, the h value was shifted from 0.5
to 1 so as to guarantee that the area involved by the interface would be adequately settled with
something like 7-10 components as recently prescribed in the project. To this point, it is noticed
that the above model and the related h/ lambda ratio esteems are not all inclusive in nature since
the interface thickness parameter term is just a relative and not supreme ratio of the real
thickness of the interface(Roldán & Gámiz 2004). During the project, there was connection in
the phase field technique to simulate two-phase flow in a smaller scale tube concentrating on
bubbly and Euler equations. In a further investigation, there was thought about the continuum
surface force (CSF) and the stage field techniques for representing the surface pressure constrain
in two-phase phase models. The two models were connected to 2-D simulation of air-water two-
phase flow in a miniaturized scale container of 600 μm distance across for the Euler and bubbly
flow equations. It was seen that the flow field anticipated by the CSF strategy was described by
expanded courses coming about because of unphysical, parasitic speed parts. Be that as it may,
this was appeared to be diminished to the dimension of machine precision by utilizing the phase
field experiment by virtue of the proper exchange of the first produced energy due to the
discretization error between the active energy and the surface pressure energy, which is in this
manner expressed as thickness(Patzold 2001). Generally few examinations in project have

connected the phase field model to think about micro scale two-phase model and among these,
scarcely any have executed a similar utilizing exercise with CFD codes. The previous point is
accepted to be a significant inadequacy given the favorable circumstances of stage field
displaying over ordinary methodologies as recorded in project report Likewise, from a simply
specialized perspective, it is very clear that business CFD codes which highlight simple model
execution alongside the alternative to change the inspection conditions according to necessity has
undoubtedly led to an ascent in their popularity for CFD applications on the loose. Explicit to
multiphase flow, this is particularly demonstrated in the solid predominance of models, for
example, the VOF and level-set in different CFD results conformed to Euler flow in micro
channels. Issues with respect to the decision of the phase field parameters have been
contemplated and examined finally. Also, certain themes of momentum look into enthusiasm for
Euler flow demonstrating that so far remain to a great extent uncertain have too been
contemplated utilizing the present model and at times considered at, ceteris paribus, with an
option VOF show.
BACKGROUND
Multiphase flow discovers their application in numerous modern stages. The most regularly
utilized system for multiphase flow is Riser reactors, Bubble section reactors Fluidized bed
reactors Scrubbers, Dryers, and so forth. A phase is characterized as a class of issue which has a
characteristic limit and an explicit unique reaction to the encompassing flow or potential field.
Stages are commonly recognized by solid, liquids or vaporous conditions of issue yet can
likewise allude to different structures e.g. particles of various size. A similar state matters with
various chemical properties are likewise called as states of matter. The fundamental motivation
behind multiphase displaying and simulation is to amplify the contact between the distinctive

stages and for boosting the uses of exchange of mass and the exchange of heat. This undertaking
concentrated on a solitary gas bubble ascending in water, in spite of the fact that similar
strategies were connected to different gas/fluid or fluid/fluid frameworks. Contingent upon air
pocket distance across, this may prompt convoluted two-phase flow. The VOF is a typical
current methodology that is reasonable for precise calculation of the liquid flow within the
ceaseless and dispersed phase, particularly if the interface indicates complex dynamical conduct.
AIM
The main aim of the project was to illustrate the multiphase flow modelling and simulation.
METHODOLOGY
MODEL OF NUMERICAL
The science for the two stage stream has been explained with the use of the equation given below
for the case of the continuity and the momentum conservation.
……….5
……………..6
The project revealed that gravity assumes an insignificant job in micro scale flow because of the
predominance of the surface pressure constrain. Further, comparable presumptions were made by
project team in separate simulation works. In like manner, in the present investigation too
powers due to gravity were dismissed(Strommer & Eichler 2001). The equivalent was checked

through evaluating more trademark generations, in the presence or absence of the gravity, though
this was considered substantial. Furthermore none connected object power as well as wellsprings
of loose power were put under the consideration. The surface strain was demonstrated as a body
constrain (FST) in the force condition. The interface following was finished by the phase field
strategy utilizing the plan as given by Eqs. 2 and 3. The stage field variable p was utilized to
administer the interface. As a tradition, in the present investigation it was risen to - 1 in the
unadulterated gas phase and +1 in unadulterated fluid phase. A scaling connection, Eq. (6), was
utilized to get the volume portion of either phase, which takes esteems from 0 to 1. The viable
liquid properties like thickness and consistency were figured as the normal estimation of the two
phase pressure by their separate volume portions acquired from Eq. 7
…………..7
Appropriate qualities for the portability and interface thickness parameters q and t were acquired
at an appropriate time size of dispersion that did not unnecessarily soggy the convective
movement but then held a steady interfacial thickness. In like manner, adequate dissemination
was to be available to oppose stressing flows that can thin or thicken the interface. So as to
acquire a physically practical arrangement, the parameter was kept up steady all through the
space. The impact of surface strain was displayed as a body constrains, FST, in the energy
condition. It was figured as the result of the synthetic capability of the framework, G, and the
bias of the phase field variable.

………………8
…………………9
COMPUTATIONAL DOMAIN
This was demonstrated in 2D with a cross flow channel setup as illustrated in Fig 1. The whole
space was discretized with a homogeneous unstructured matrix comprising of triangular
components. To keep up consistent goals of the gas-fluid interface all through the channel, the
whole space was discretized utilizing the comparable measured components. In this manner it
was impractical to utilize a square organized framework with refined work goals close to the
channel walls..
Figure 1: Flow channel (Robinson 2008)
The channels were displayed with a consistent speed limit condition with a solitary phase being
conceded through every channel. A pressure based outpouring limit condition was indicated at
the outlet of the micro channel which indicated a Dirichlet condition on the pressure alongside a
vanishing gooey pressure(Robinson 2008). For the channel walls, no-slip, free-slip or wetted-

wall conditions were material and a close investigation was embraced between them. The last
was executed by determining a static contact point in Eq. (10), in which the right-hand-side
equation is generally displayed as zero for the free-slip/no-slip cases.
An understood time-project calculation was utilized to get the numerical calculations. The phase
field factors were introduced by specifically tackling the two parameters. This transient
introduction was utilized to make the interface. Since the channel was at first thought to be
loaded up with quiet vaporous phase, the underlying interface was framed at the fluid delta. It
was guaranteed for each simulation that the interface made by the introduction method was
monotonic and was dependably within the permitted scope of - 1 to +1. The last transient
simulation was tackled for all the administering conditions utilizing the underlying qualities
shown above. The resistance criteria for the residuals were set to a request size lower than the
solver's default esteems. All simulations were completed on a Dell Precision T5500 workstation
containing two Intel Xeon processors with eight centers, 4 GB of RAM and a Windows 7 32-bit
operating system..
RESULTS AND DISCUSSION
Grid independence
The affectability of the answer for the area discretization (spatial work component type and size)
was considered by checking the gas void division and the air pocket/slug lengths. So as to keep
up steady goals of the interface all through, the estimation of the interface thickness parameter,
was to be close to the component measure, h, in the position possessed by the interface.

Additionally the project team suggested at minimum 7-10 framework components to be available
in the interfacial region to get adequate goals. Since the client characterized estimation of values
in this examination fills in as a general proportion of the interface thickness just and not as an
outright measure.
The range for the h/lambda ratio (between 0.5 to 1) proposed by the project team couldn't be
specifically used in this investigation. Subsequently h/k values going from solidarity until the
point that two were explored as two extraordinary cases. The position inside 0.996 volume part
of vaporous phase (0.004 volume part of fluid stage) was considered to be characterized as the
'interfacial area' for this investigation. For a h/p ratio of unity, it was settled by in excess of 15
components while for a ratio estimation of 2, it was just shy of 10 components. Both these cases
exist in the other literature works. Be that as it may, as found in Fig. 2, better network
independency was obtained with an estimation of solidness for the h/k ratio when contrasted with
an estimation of 2, and consequently the previous one was determined for every further
simulations. The project reports that quadrilateral cells perform better as contrasted with
triangular components as for limiting errors(Picard, DiGioia, Moody & Jaramaz 2003).
These discoveries have been founded on interface following utilization of finite volume usage of
the VOF technique . Subsequently, a similar affectability was assessed for the present finite
element usage of the phase field technique. The current displaying results were observed to be
totally obtuse of the component type. However, the triangular components brought about a
decrease in computational time by almost 20% when contrasted with the quadrilateral
components and thus it was the favored decision in this investigation. This little contrast in
computational time could be ascribed to the reality that the greatest component skewness for the
quadrilateral cells was somewhat higher (0.13) than that for the triangular cells (0.08). The low

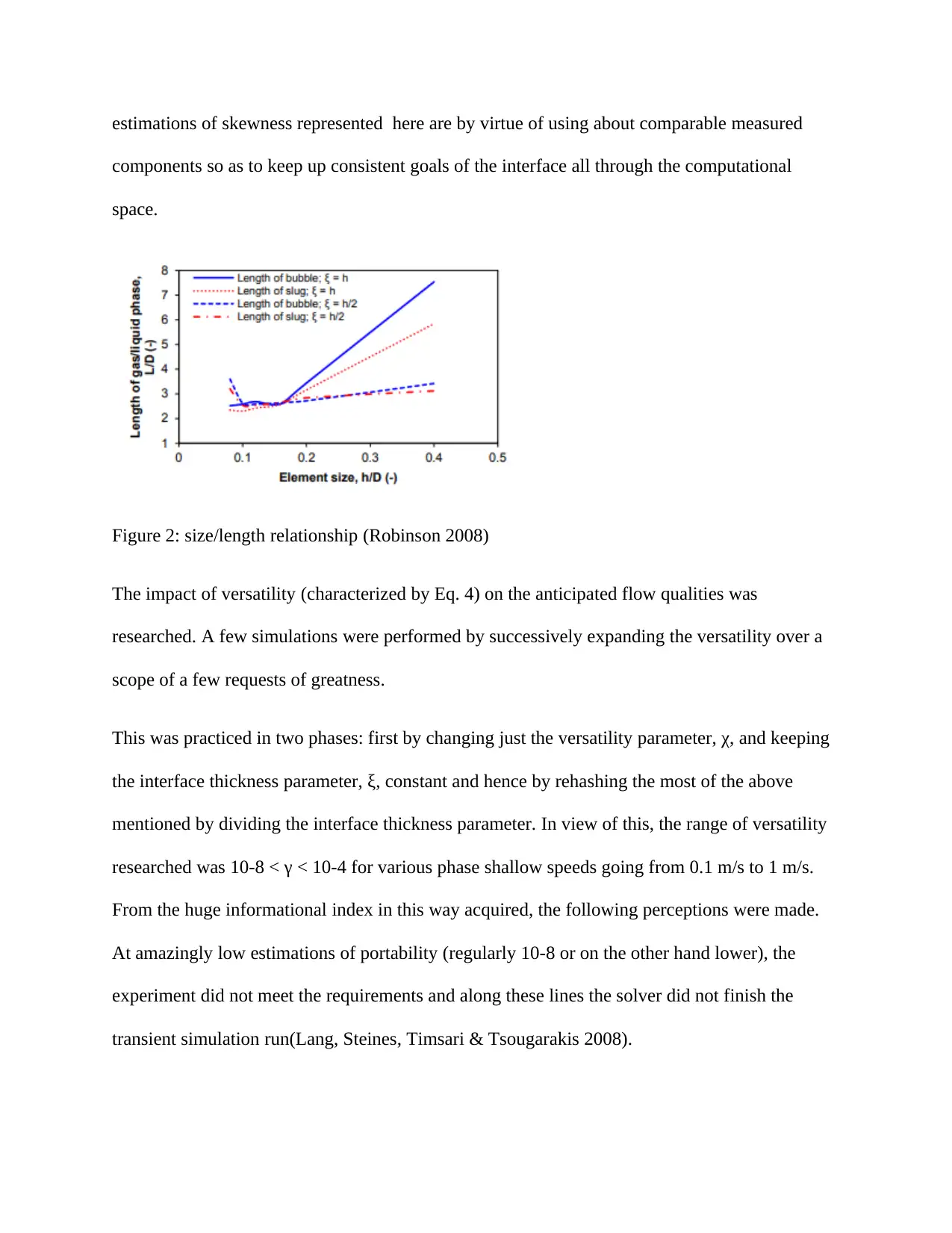
estimations of skewness represented here are by virtue of using about comparable measured
components so as to keep up consistent goals of the interface all through the computational
space.
Figure 2: size/length relationship (Robinson 2008)
The impact of versatility (characterized by Eq. 4) on the anticipated flow qualities was
researched. A few simulations were performed by successively expanding the versatility over a
scope of a few requests of greatness.
This was practiced in two phases: first by changing just the versatility parameter, χ, and keeping
the interface thickness parameter, ξ, constant and hence by rehashing the most of the above
mentioned by dividing the interface thickness parameter. In view of this, the range of versatility
researched was 10-8 < γ < 10-4 for various phase shallow speeds going from 0.1 m/s to 1 m/s.
From the huge informational index in this way acquired, the following perceptions were made.
At amazingly low estimations of portability (regularly 10-8 or on the other hand lower), the
experiment did not meet the requirements and along these lines the solver did not finish the
transient simulation run(Lang, Steines, Timsari & Tsougarakis 2008).