Advanced Macroeconomics Study Material

This study material provides advanced macroeconomics content including solved assignments, essays, and dissertations. It covers topics such as optimization issues faced by representative agents, population growth equations, Solow Model of Development, and the dynamics of capital stock per capita.

Advanced
Macroeconomics

Contents
Question 1........................................................................................................................................4
Question 2........................................................................................................................................5
Question 3........................................................................................................................................6
Question 4........................................................................................................................................8

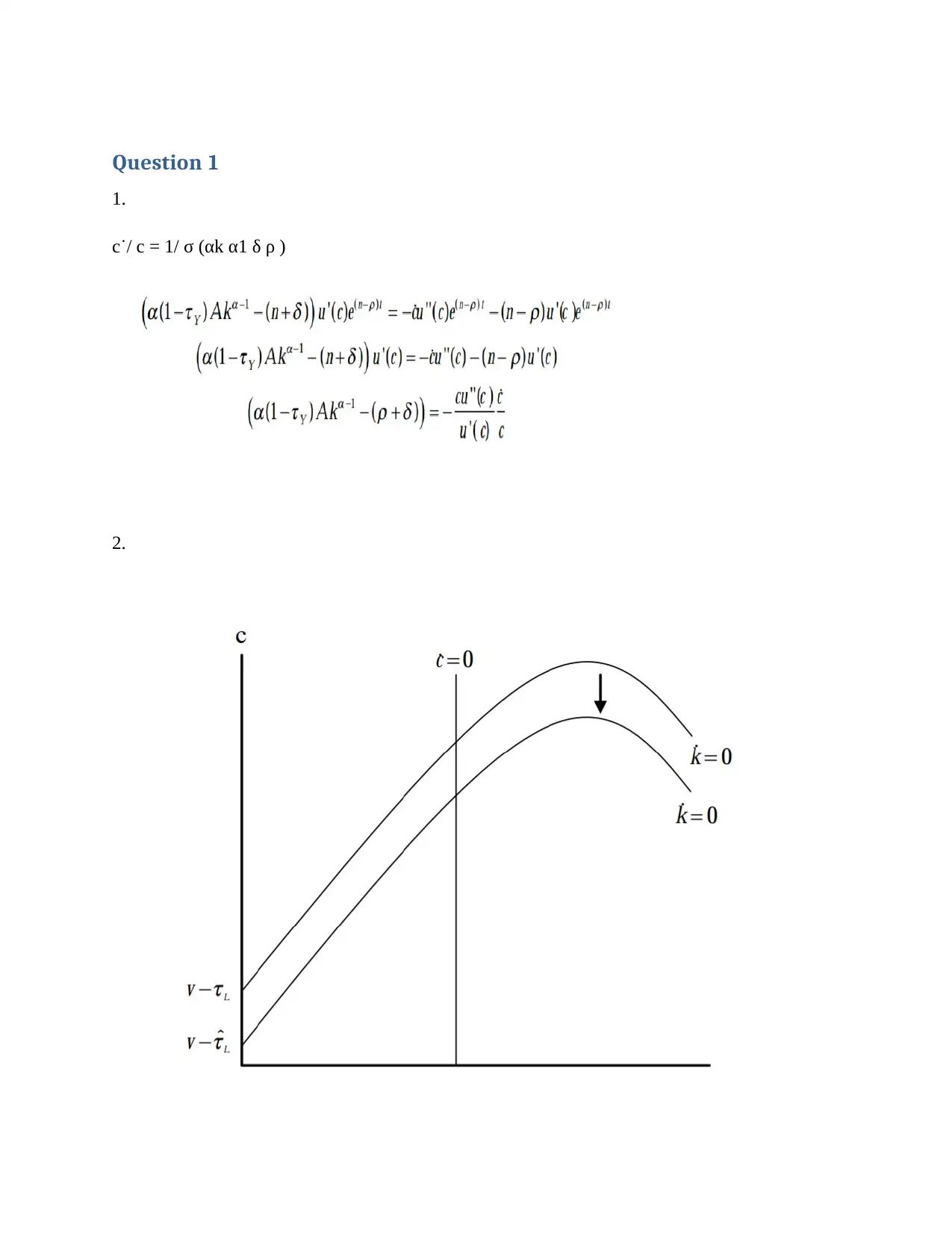
Question 1
1.
c˙/ c = 1/ σ (αk α1 δ ρ )
2.

3. Increased need for rehabilitation and restoration services is accompanied by cost increases in
all global disasters. Our model presupposes normal post-disaster rate inflations assumptions,
although demand-driven inflation becomes highly non-linear, and cost acceleration could make
catastrophe much cheaper even under pessimistic conditions and dramatically improve recovery
time, all of which will have a larger effect on financial stocks.
Question 2
The optimization issue faced by representative-agent:
Here, λt is Langrangian multipliers linked with resource’s constraint. There first orders condition
is ct : 1 ct = λt

Question 3
The number of people is rising increasingly g. Thus the, current (N) population and potential (N')
population are related by means of population growth equation, here N'= N(1+g). There is no
change in population growth equation. When the population now is 100 and population growth-
rate is 2 percent, the population for future is 102. Both customers save their wages, "s" and spend
the majority in the market, a steady proportion. consumption formula C = (1+s)Y is thus
intertwined between consumption (expressed by C) and production (expressed by Y). When a
consumer receives 100 units of outputs as profits, and savings rates of 40 percent, consumer
consumes sixty units as well as saves forty.
All enterprises in economy generate production that use same production technologies as
supplies in capital funds as well as labour. There are also the output scale (expressed by Y).
Here, production function expression Y = aF is level of capital (expressed by K), and work level
(expressed by L). Solow Model of Development suggests the output function is continuously
restored (CRS). In this respect, when we double that of our supplies of capital fund and double
that of our labour, we double that of our production. The statistical study of Solow model thus

emphasizes on production per employee and resources per employee rather than on combined
production and capital stocks.
Existing stocks of capital (expressed by K), potential stocks of capital (expressed by K,')
including capital depreciation levels (expressed by d) are related to equity accruals K'=K(1-d) +
I.
In this analysis, we presume the following type of output function: Y = aKbL1-b whereby 0 < b
< 1. The manufacturing pattern is defined as Cobb-Douglas Productions, neoclassical production
function that is used more extensively. In accordance with the presumption that corporations are
competitive, namely the pricing companies, the b-coffector is share stock. Thus the, worker
performance is provided in following equation: y = akb, whereby y = Y/L (workers output and k
= K/L) (capital stock per worker) (capital stock per worker)
We have the below under the presumption of competitive balance:
Identity of income-expenditure as state of balance: Y = C + I
Budget restraint of the consumer: Y = C + S
So at balance: I = S = sY. So at balance.
The expression of capital accumulation has become:
The equation for capital accumulation throughout the time of the workers is given as follows: (1
+ g)k' = (1 – d)k + sy = (1 – d)k + saf(k) = (1 – d)k + sakb
The definition of solutions used is a lasting one. The constant condition is a state in which capital
level per employee does not alter. Take the following diagram:

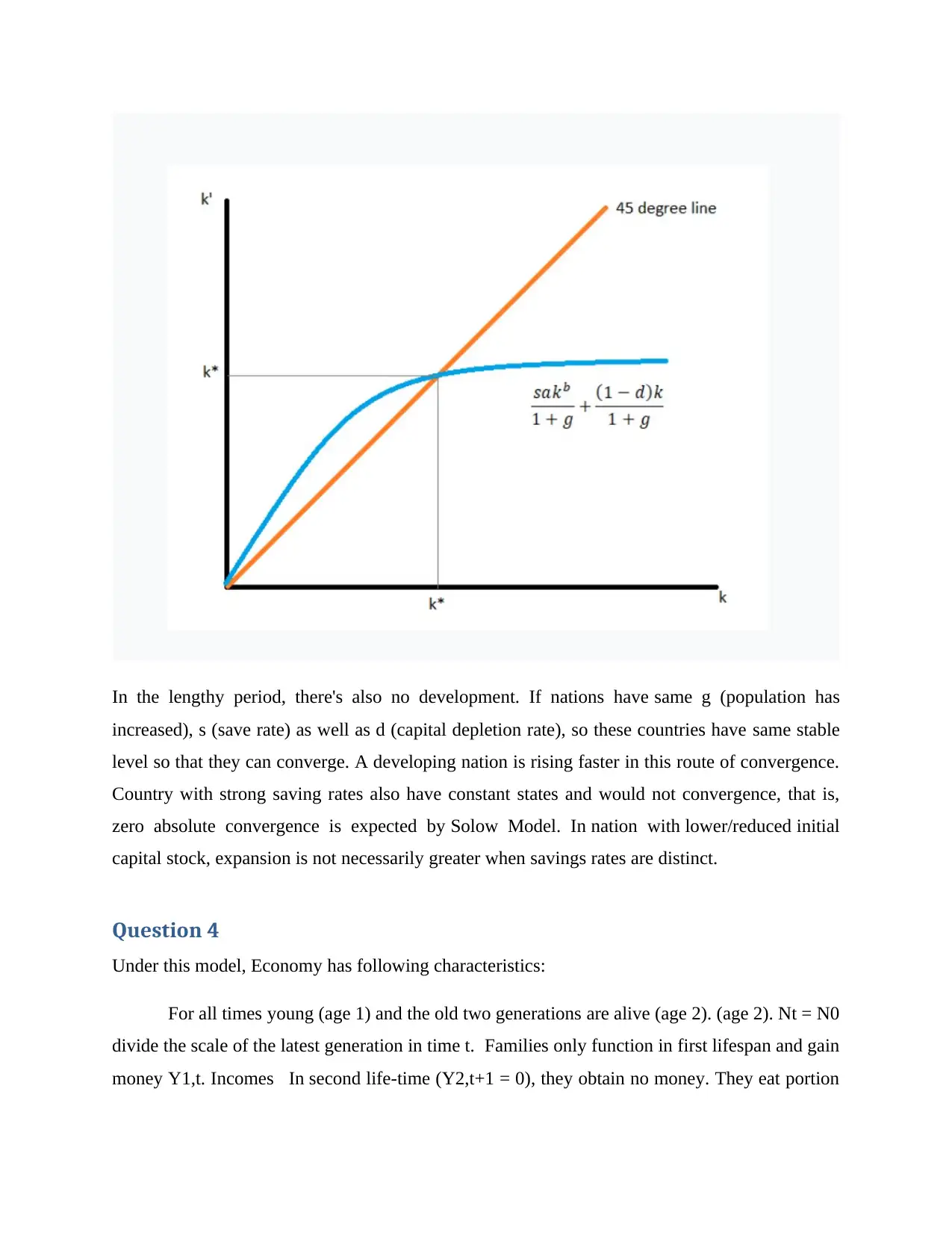
In the lengthy period, there's also no development. If nations have same g (population has
increased), s (save rate) as well as d (capital depletion rate), so these countries have same stable
level so that they can converge. A developing nation is rising faster in this route of convergence.
Country with strong saving rates also have constant states and would not convergence, that is,
zero absolute convergence is expected by Solow Model. In nation with lower/reduced initial
capital stock, expansion is not necessarily greater when savings rates are distinct.
Question 4
Under this model, Economy has following characteristics:
For all times young (age 1) and the old two generations are alive (age 2). (age 2). Nt = N0
divide the scale of the latest generation in time t. Families only function in first lifespan and gain
money Y1,t. Incomes In second life-time (Y2,t+1 = 0), they obtain no money. They eat portion

from their first cycle earnings and save balance until they are old to fund their consumptions.
The resources of young at end of time t are the origins of the resources used throughout period
t+1, Kt+1=Nta1,t for overall output while a1,t are assets per young households after consumption
in cycle 1. (We conclude that depreciation also isn't available for convenience). Older in period t
holds the whole share and (as they have zero inheritance motive) absorbs all, thus, the older in
period t becomes Nt‐1a1,t‐1 = Kt. The older would be dissolved by the older (The old people get
interest on capital and thus spending would be Kt including interest income, however saving
would not impact the rKt portion since it is an integrated component of incomes and
consumptions). Capital and labour economies remain perfectly competitive as well as the
aggregate new technologies is CRS, Y = F(K, L) (note that F(K, L) = F(K, L). FLL + FKK). Let
young populations Nt normalise all, write normalised variables in lowered case. Thus the overall
output feature per young person is translated into:
f(kt) ≡ F(Kt ,Nt)/Nt = F(Kt/Nt , 1)
The presumption of perfectly competitive means that wages as well as net interests rates
contribute respectively to margins of labour and capital:
Wt = f(kt) − kt f 0 (kt), rt = f0 (kt)
We have to make clear decisions regarding utility function as well as the overall output
functions to make more progress. Assuming the utility to be CRRA, u(•) = • 1−р/(1 − − ̈ ) and
assuming the net output of Cobb-Douglas F[K, L] = CL 1−р − for the production feature f[ k]
Throughout this case it is possible to solve the following:

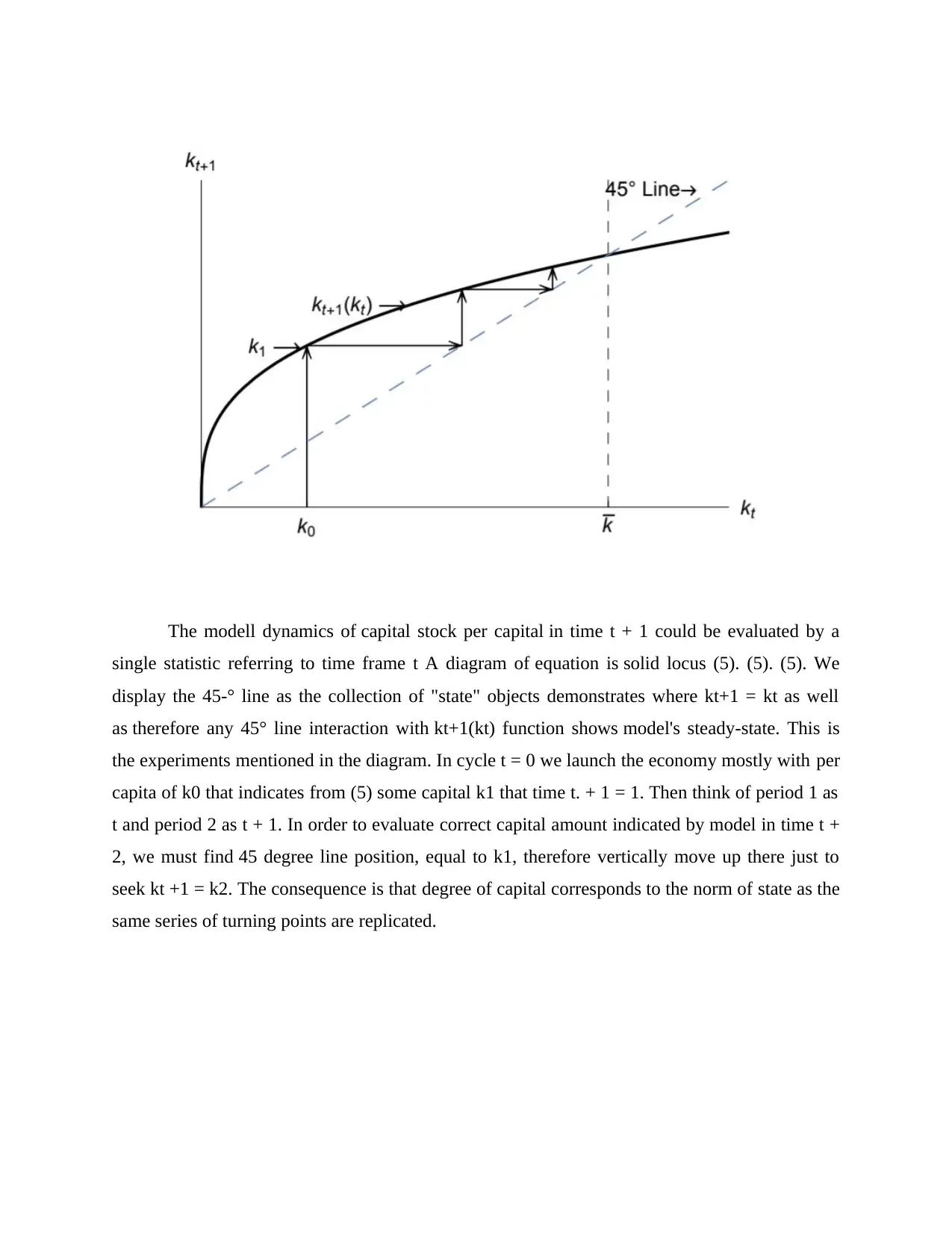
The modell dynamics of capital stock per capital in time t + 1 could be evaluated by a
single statistic referring to time frame t A diagram of equation is solid locus (5). (5). (5). We
display the 45-° line as the collection of "state" objects demonstrates where kt+1 = kt as well
as therefore any 45° line interaction with kt+1(kt) function shows model's steady-state. This is
the experiments mentioned in the diagram. In cycle t = 0 we launch the economy mostly with per
capita of k0 that indicates from (5) some capital k1 that time t. + 1 = 1. Then think of period 1 as
t and period 2 as t + 1. In order to evaluate correct capital amount indicated by model in time t +
2, we must find 45 degree line position, equal to k1, therefore vertically move up there just to
seek kt +1 = k2. The consequence is that degree of capital corresponds to the norm of state as the
same series of turning points are replicated.