CO5124: Data Analysis & Decision Modelling - Golf Resort Proposal
VerifiedAdded on 2023/03/31
|10
|1972
|147
Case Study
AI Summary
This case study involves applying data analysis and decision modeling techniques to the Cunningham Gudgal Golf Resort project. The primary objective is to maximize player enjoyment while adhering to various constraints, including budget limitations, acreage requirements, and the number of holes and their par values. The analysis explores different scenarios, such as incorporating a standard or exclusive clubhouse and adjusting construction costs or project budgets. Linear programming models are formulated and analyzed using Excel Solver to determine the optimal golf hole configuration for each scenario. The study evaluates the feasibility and outcomes of different management plans and shareholder proposals, providing insights into the decision-making process for the golf resort development. The assignment uses the course code CO5124 - Data Analysis and Decision Modelling.

Part 1: Action Plan
1. Decision variables
These are the variables that need to be altered so as to optimize the objective function. In
this analysis, the decision variable is the golf hole configuration. Let x represent the
number of golf holes; then
x1=Straight par 5
x2=Dogleg par 5
x3=Straight par 4
x4 =Dogleg par 4
x5=long par 3
x6=Short par 3
2. Objective function
This is the function that need to be optimised. The objective function for this linear
programming is the total enjoyment index.
3. Constraints
The constraints of a linear programming are the set conditions that must be adhered to by
the linear program for its output to be classified as feasible.
The constraints are listed below;
The total construction cost should not exceed $ 20 million.
The acreage of the golf resort needs to be between 36 and 42.
The number of pars for all the golf holes ought to be between 70 and 72.
Total golf holes to be constructed are to be 18.
Par 5 should not exceed 4
Par 4 should not exceed 14.
Par 3 should not exceed 4.
Straight par 5 should not be less than 1
Dogleg oar 5 should not be less than 1
Straight oar 4 should not be less than 2.
1. Decision variables
These are the variables that need to be altered so as to optimize the objective function. In
this analysis, the decision variable is the golf hole configuration. Let x represent the
number of golf holes; then
x1=Straight par 5
x2=Dogleg par 5
x3=Straight par 4
x4 =Dogleg par 4
x5=long par 3
x6=Short par 3
2. Objective function
This is the function that need to be optimised. The objective function for this linear
programming is the total enjoyment index.
3. Constraints
The constraints of a linear programming are the set conditions that must be adhered to by
the linear program for its output to be classified as feasible.
The constraints are listed below;
The total construction cost should not exceed $ 20 million.
The acreage of the golf resort needs to be between 36 and 42.
The number of pars for all the golf holes ought to be between 70 and 72.
Total golf holes to be constructed are to be 18.
Par 5 should not exceed 4
Par 4 should not exceed 14.
Par 3 should not exceed 4.
Straight par 5 should not be less than 1
Dogleg oar 5 should not be less than 1
Straight oar 4 should not be less than 2.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Dogleg par 4 should not be less than 2
Long par 3 should not be less than 1
Short par 3 should not be less than 1
Also, another constraint that need to be accounted for is the type of clubhouse to be
constructed. Let a clubhouse be denoted by z. then;
z1=Standard clubhouse
z2=Exclusive clubhouse
4. Mathematical expressions
The objective function and the constraints will be modelled as mathematical equations for
each of the models created.
Managers plan
In this plan the clubhouse to be included is the standard clubhouse at a cost of $ 3.5
million covering 2 hectares.
The model plan
Max ; 2 x1 +1.5 x2 +1.5 x3+2 x4 +1.75 x5+2.25 x6
Subjects to the constraints
x1 ≥ 1
x2 ≥ 1
x3 ≥ 2
x4 ≥2
x5 ≥ 1
x6 ≥ 1
x1+ x2 ≤ 4
x3+ x4 ≤ 1 4
x5+ x6 ≤ 4
x1+ x2 +x3 + x4 + x5+ x6 =18
Long par 3 should not be less than 1
Short par 3 should not be less than 1
Also, another constraint that need to be accounted for is the type of clubhouse to be
constructed. Let a clubhouse be denoted by z. then;
z1=Standard clubhouse
z2=Exclusive clubhouse
4. Mathematical expressions
The objective function and the constraints will be modelled as mathematical equations for
each of the models created.
Managers plan
In this plan the clubhouse to be included is the standard clubhouse at a cost of $ 3.5
million covering 2 hectares.
The model plan
Max ; 2 x1 +1.5 x2 +1.5 x3+2 x4 +1.75 x5+2.25 x6
Subjects to the constraints
x1 ≥ 1
x2 ≥ 1
x3 ≥ 2
x4 ≥2
x5 ≥ 1
x6 ≥ 1
x1+ x2 ≤ 4
x3+ x4 ≤ 1 4
x5+ x6 ≤ 4
x1+ x2 +x3 + x4 + x5+ x6 =18

3 x1+3.5 x2 +2 x3 +2,5 x4 +1 x5 +0.75 x6 +2 z1 ≤ 42
3 x1+3.5 x2 +2 x3 +2,5 x4 +1 x5 +0.75 x6 +2 z1 ≥36
1000000 x1 +1500000 x2+750000 x3 +900000 x4 +600000 x5 +650000 x6 +3500000 z1 ≤20000000
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≤ 72
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≥70
When these details are modelled in excel, we obtain the model as summarized by the
table below.
Cunningham Golf Resort
Straight par 5 Dogleg par 5 Straight par 4 Dogleg par 4 Long par 3 Short par 3
Par 5 5 8 40 3 9
Size 3 3.5 4 25 1 2.25
Enjoyment Index 2 1.5 3 20 1.75 6.75
Construction cost $1,000,000 $1,500,000 $1,500,000 $9,000,000 $600,000 $1,950,000
Number 1 1 2 10 1 3
>= >= >= >= >= >=
1 1 2 2 1 1
Clubhouse
Standard
Cost $3,500,000
Size 2
Enjoyment Index 0
Objective Function
Total Enjoyment Index 35
Constraints
Par 5 2 <= 4
Par 4 12 <= 14
Par 3 4 <= 4
Total Size 40.75 <= 42
Total Size 40.75 >= 36
Total Cost $19,050,000 <= $20,000,000
Total Par 70 <= 72
Total Par 70 >= 70
Number of holes 18 = 18
Shareholders plan
In the shareholders plan, the golf resort is to include an exclusive warehouse constructed
at a cost of $ 6 million and covering an area of 4 hectares.
3 x1+3.5 x2 +2 x3 +2,5 x4 +1 x5 +0.75 x6 +2 z1 ≥36
1000000 x1 +1500000 x2+750000 x3 +900000 x4 +600000 x5 +650000 x6 +3500000 z1 ≤20000000
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≤ 72
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≥70
When these details are modelled in excel, we obtain the model as summarized by the
table below.
Cunningham Golf Resort
Straight par 5 Dogleg par 5 Straight par 4 Dogleg par 4 Long par 3 Short par 3
Par 5 5 8 40 3 9
Size 3 3.5 4 25 1 2.25
Enjoyment Index 2 1.5 3 20 1.75 6.75
Construction cost $1,000,000 $1,500,000 $1,500,000 $9,000,000 $600,000 $1,950,000
Number 1 1 2 10 1 3
>= >= >= >= >= >=
1 1 2 2 1 1
Clubhouse
Standard
Cost $3,500,000
Size 2
Enjoyment Index 0
Objective Function
Total Enjoyment Index 35
Constraints
Par 5 2 <= 4
Par 4 12 <= 14
Par 3 4 <= 4
Total Size 40.75 <= 42
Total Size 40.75 >= 36
Total Cost $19,050,000 <= $20,000,000
Total Par 70 <= 72
Total Par 70 >= 70
Number of holes 18 = 18
Shareholders plan
In the shareholders plan, the golf resort is to include an exclusive warehouse constructed
at a cost of $ 6 million and covering an area of 4 hectares.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

The model plan
Max ; 2 x1 +1.5 x2 +1.5 x3+2 x4 +1.75 x5+2.25 x6+4 z2
Subjects to the constraints
x1 ≥ 1
x2 ≥ 1
x3 ≥ 2
x4 ≥2
x5 ≥ 1
x6 ≥ 1
x1+ x2 ≤ 4
x3+ x4 ≤ 14
x5+ x6 ≤ 4
x1+ x2 +x3 + x4 + x5+ x6 =18
3 x1+3.5 x2 +2 x3 +2,5 x4 +1 x5 +0.75 x6 +4 z2 ≤ 42
3 x1+3.5 x2 +2 x3 +2,5 x4 +1 x5 +0.75 x6 +4 z2 ≥36
1000000 x1 +1500000 x2+750000 x3 +900000 x4 +600000 x5 +650000 x6 +60 00000 z2 ≤20000000
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≤ 72
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≥70
The model is summarized below (no feasible solution)
Max ; 2 x1 +1.5 x2 +1.5 x3+2 x4 +1.75 x5+2.25 x6+4 z2
Subjects to the constraints
x1 ≥ 1
x2 ≥ 1
x3 ≥ 2
x4 ≥2
x5 ≥ 1
x6 ≥ 1
x1+ x2 ≤ 4
x3+ x4 ≤ 14
x5+ x6 ≤ 4
x1+ x2 +x3 + x4 + x5+ x6 =18
3 x1+3.5 x2 +2 x3 +2,5 x4 +1 x5 +0.75 x6 +4 z2 ≤ 42
3 x1+3.5 x2 +2 x3 +2,5 x4 +1 x5 +0.75 x6 +4 z2 ≥36
1000000 x1 +1500000 x2+750000 x3 +900000 x4 +600000 x5 +650000 x6 +60 00000 z2 ≤20000000
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≤ 72
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≥70
The model is summarized below (no feasible solution)
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Cunningham Golf Resort
Straight par 5 Dogleg par 5 Straight par 4 Dogleg par 4 Long par 3 Short par 3
Par 5 5 38.66666667 8 9 3
Size 3 3.5 19.33333333 5 3 0.75
Enjoyment Index 2 1.5 14.5 4 5.25 2.25
Construction cost $1,000,000 $1,500,000 $7,250,000 $1,800,000 $1,800,000 $650,000
Number 1 1 9.666666667 2 3 1
>= >= >= >= >= >=
1 1 2 2 1 1
Clubhouse
Exclusive
Cost $6,000,000
Size 4
Enjoyment Index 4
Objective Function
Total Enjoyment Index 33.5
Constraints
Par 5 2 <= 4
Par 4 11.66666667 <= 14
Par 3 4 <= 4
Total Size 38.58333333 <= 42
Total Size 38.58333333 >= 36
Total Cost $20,000,000 <= $20,000,000
Total Par 68.66666667 <= 72
Total Par 68.66666667 >= 70
Number of holes 17.66666667 = 18
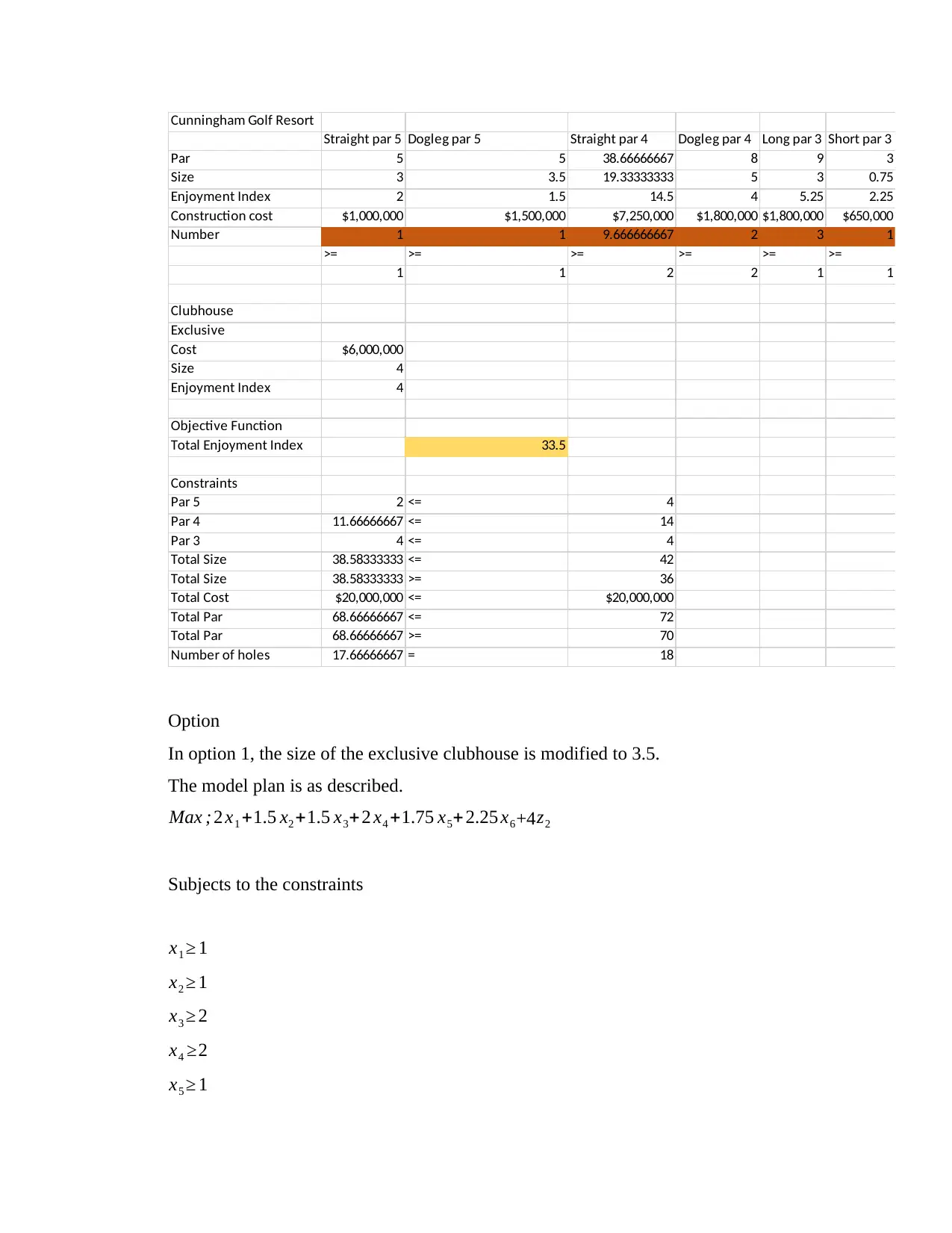
Option
In option 1, the size of the exclusive clubhouse is modified to 3.5.
The model plan is as described.
Max ; 2 x1 +1.5 x2 +1.5 x3+2 x4 +1.75 x5+2.25 x6+4z2
Subjects to the constraints
x1 ≥ 1
x2 ≥ 1
x3 ≥ 2
x4 ≥2
x5 ≥ 1
Straight par 5 Dogleg par 5 Straight par 4 Dogleg par 4 Long par 3 Short par 3
Par 5 5 38.66666667 8 9 3
Size 3 3.5 19.33333333 5 3 0.75
Enjoyment Index 2 1.5 14.5 4 5.25 2.25
Construction cost $1,000,000 $1,500,000 $7,250,000 $1,800,000 $1,800,000 $650,000
Number 1 1 9.666666667 2 3 1
>= >= >= >= >= >=
1 1 2 2 1 1
Clubhouse
Exclusive
Cost $6,000,000
Size 4
Enjoyment Index 4
Objective Function
Total Enjoyment Index 33.5
Constraints
Par 5 2 <= 4
Par 4 11.66666667 <= 14
Par 3 4 <= 4
Total Size 38.58333333 <= 42
Total Size 38.58333333 >= 36
Total Cost $20,000,000 <= $20,000,000
Total Par 68.66666667 <= 72
Total Par 68.66666667 >= 70
Number of holes 17.66666667 = 18
Option
In option 1, the size of the exclusive clubhouse is modified to 3.5.
The model plan is as described.
Max ; 2 x1 +1.5 x2 +1.5 x3+2 x4 +1.75 x5+2.25 x6+4z2
Subjects to the constraints
x1 ≥ 1
x2 ≥ 1
x3 ≥ 2
x4 ≥2
x5 ≥ 1
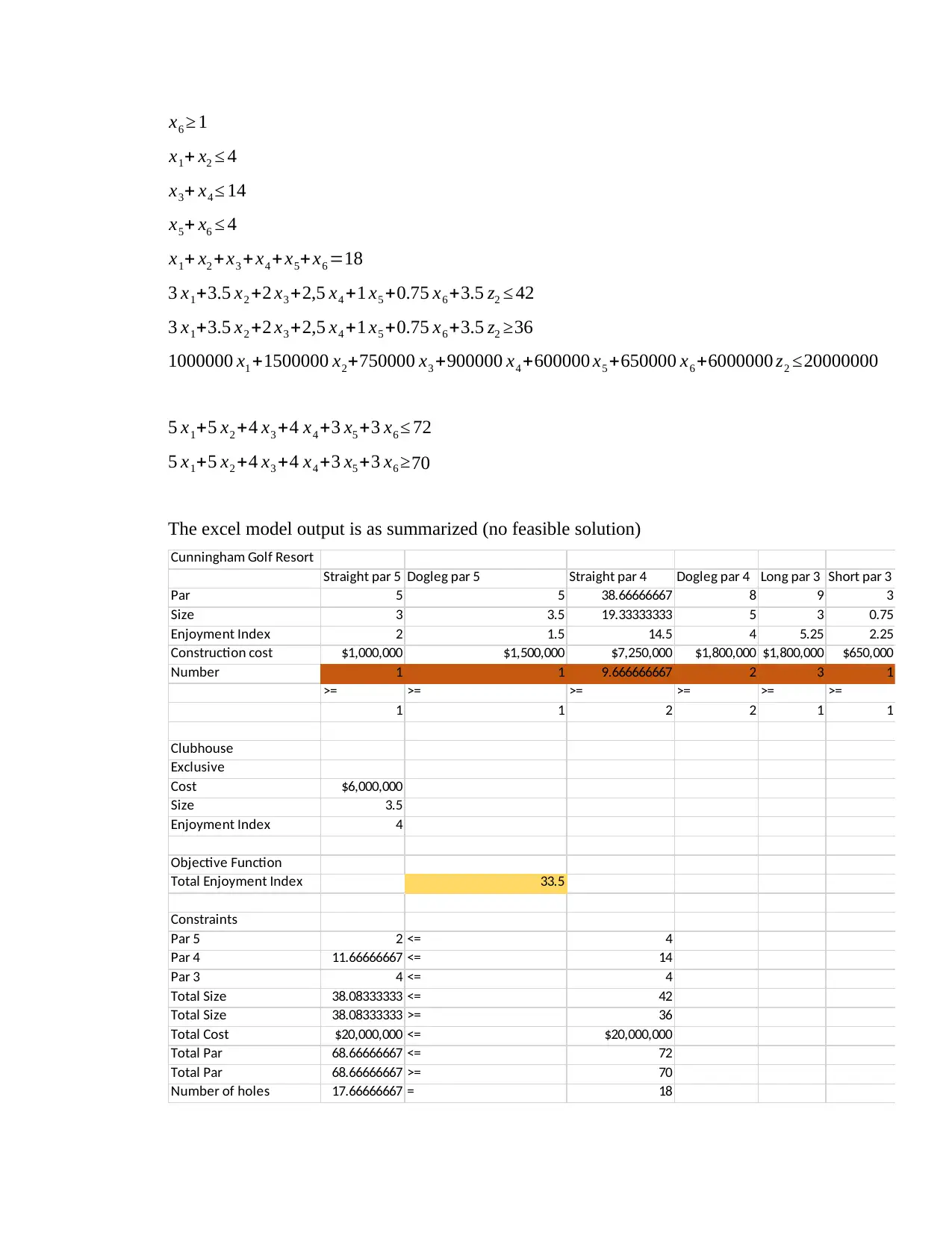
x6 ≥ 1
x1+ x2 ≤ 4
x3+ x4 ≤ 14
x5+ x6 ≤ 4
x1+ x2 +x3 + x4 + x5+ x6 =18
3 x1+3.5 x2 +2 x3 +2,5 x4 +1 x5 +0.75 x6 +3.5 z2 ≤ 42
3 x1+3.5 x2 +2 x3 +2,5 x4 +1 x5 +0.75 x6 +3.5 z2 ≥36
1000000 x1 +1500000 x2+750000 x3 +900000 x4 +600000 x5 +650000 x6 +6000000 z2 ≤20000000
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≤ 72
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≥70
The excel model output is as summarized (no feasible solution)
Cunningham Golf Resort
Straight par 5 Dogleg par 5 Straight par 4 Dogleg par 4 Long par 3 Short par 3
Par 5 5 38.66666667 8 9 3
Size 3 3.5 19.33333333 5 3 0.75
Enjoyment Index 2 1.5 14.5 4 5.25 2.25
Construction cost $1,000,000 $1,500,000 $7,250,000 $1,800,000 $1,800,000 $650,000
Number 1 1 9.666666667 2 3 1
>= >= >= >= >= >=
1 1 2 2 1 1
Clubhouse
Exclusive
Cost $6,000,000
Size 3.5
Enjoyment Index 4
Objective Function
Total Enjoyment Index 33.5
Constraints
Par 5 2 <= 4
Par 4 11.66666667 <= 14
Par 3 4 <= 4
Total Size 38.08333333 <= 42
Total Size 38.08333333 >= 36
Total Cost $20,000,000 <= $20,000,000
Total Par 68.66666667 <= 72
Total Par 68.66666667 >= 70
Number of holes 17.66666667 = 18
x1+ x2 ≤ 4
x3+ x4 ≤ 14
x5+ x6 ≤ 4
x1+ x2 +x3 + x4 + x5+ x6 =18
3 x1+3.5 x2 +2 x3 +2,5 x4 +1 x5 +0.75 x6 +3.5 z2 ≤ 42
3 x1+3.5 x2 +2 x3 +2,5 x4 +1 x5 +0.75 x6 +3.5 z2 ≥36
1000000 x1 +1500000 x2+750000 x3 +900000 x4 +600000 x5 +650000 x6 +6000000 z2 ≤20000000
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≤ 72
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≥70
The excel model output is as summarized (no feasible solution)
Cunningham Golf Resort
Straight par 5 Dogleg par 5 Straight par 4 Dogleg par 4 Long par 3 Short par 3
Par 5 5 38.66666667 8 9 3
Size 3 3.5 19.33333333 5 3 0.75
Enjoyment Index 2 1.5 14.5 4 5.25 2.25
Construction cost $1,000,000 $1,500,000 $7,250,000 $1,800,000 $1,800,000 $650,000
Number 1 1 9.666666667 2 3 1
>= >= >= >= >= >=
1 1 2 2 1 1
Clubhouse
Exclusive
Cost $6,000,000
Size 3.5
Enjoyment Index 4
Objective Function
Total Enjoyment Index 33.5
Constraints
Par 5 2 <= 4
Par 4 11.66666667 <= 14
Par 3 4 <= 4
Total Size 38.08333333 <= 42
Total Size 38.08333333 >= 36
Total Cost $20,000,000 <= $20,000,000
Total Par 68.66666667 <= 72
Total Par 68.66666667 >= 70
Number of holes 17.66666667 = 18
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Option 2
In option 2 the construction cost of the model is reduced to $ 5 million.
The model plan
Max ; 2 x1 +1.5 x2 +1.5 x3+2 x4 +1.75 x5+2.25 x6+4 z2
Subjects to the constraints
x1 ≥ 1
x2 ≥ 1
x3 ≥ 2
x4 ≥2
x5 ≥ 1
x6 ≥ 1
x1+ x2 ≤ 4
x3+ x4 ≤ 14
x5+ x6 ≤ 4
x1+ x2 +x3 + x4 + x5+ x6 =18
3 x1+3.5 x2 +2 x3 +2,5 x4 +1 x5 +0.75 x6 +3.5 z2 ≤ 42
3 x1+3.5 x2 +2 x3 +2,5 x4 +1 x5 +0.75 x6 +3.5 z2 ≥36
1000000 x1 +1500000 x2+750000 x3 +900000 x4 +600000 x5 +650000 x6 +5 000000 z2 ≤20000000
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≤ 72
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≥70
The model output
In option 2 the construction cost of the model is reduced to $ 5 million.
The model plan
Max ; 2 x1 +1.5 x2 +1.5 x3+2 x4 +1.75 x5+2.25 x6+4 z2
Subjects to the constraints
x1 ≥ 1
x2 ≥ 1
x3 ≥ 2
x4 ≥2
x5 ≥ 1
x6 ≥ 1
x1+ x2 ≤ 4
x3+ x4 ≤ 14
x5+ x6 ≤ 4
x1+ x2 +x3 + x4 + x5+ x6 =18
3 x1+3.5 x2 +2 x3 +2,5 x4 +1 x5 +0.75 x6 +3.5 z2 ≤ 42
3 x1+3.5 x2 +2 x3 +2,5 x4 +1 x5 +0.75 x6 +3.5 z2 ≥36
1000000 x1 +1500000 x2+750000 x3 +900000 x4 +600000 x5 +650000 x6 +5 000000 z2 ≤20000000
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≤ 72
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≥70
The model output
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Cunningham Golf Resort
Straight par 5 Dogleg par 5 Straight par 4 Dogleg par 4 Long par 3 Short par 3
Par 5 5 24 24 3 9
Size 3 3.5 12 15 1 2.25
Enjoyment Index 2 1.5 9 12 1.75 6.75
Construction cost $1,000,000 $1,500,000 $4,500,000 $5,400,000 $600,000 $1,950,000
Number 1 1 6 6 1 3
>= >= >= >= >= >=
1 1 2 2 1 1
Clubhouse
Exclusive
Cost $5,000,000
Size 4
Enjoyment Index 4
Objective Function
Total Enjoyment Index 37
Constraints
Par 5 2 <= 4
Par 4 12 <= 14
Par 3 4 <= 4
Total Size 40.75 <= 42
Total Size 40.75 >= 36
Total Cost $19,950,000 <= $20,000,000
Total Par 70 <= 72
Total Par 70 >= 70
Number of holes 18 = 18
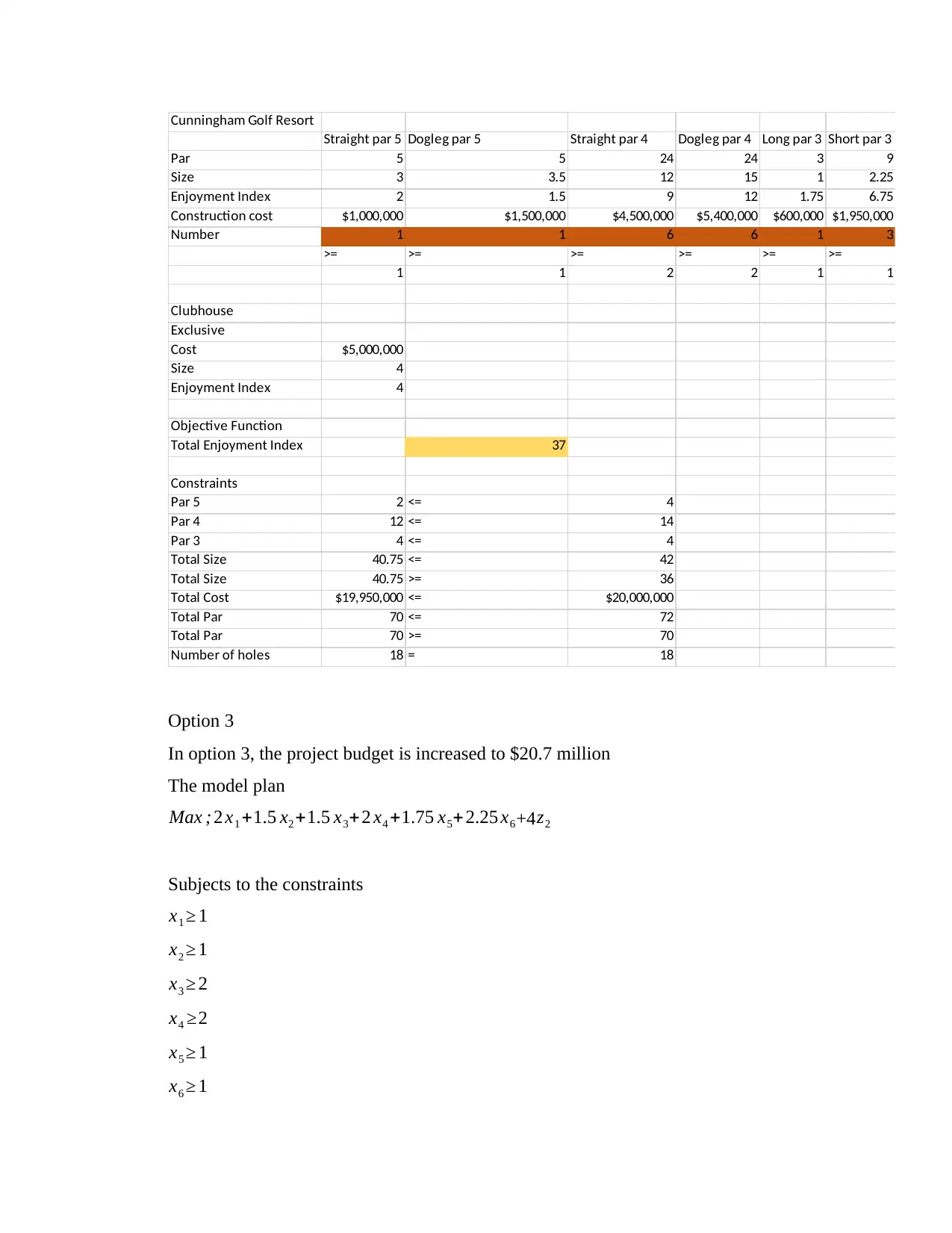
Option 3
In option 3, the project budget is increased to $20.7 million
The model plan
Max ; 2 x1 +1.5 x2 +1.5 x3+2 x4 +1.75 x5+2.25 x6+4z2
Subjects to the constraints
x1 ≥ 1
x2 ≥ 1
x3 ≥ 2
x4 ≥2
x5 ≥ 1
x6 ≥ 1
Straight par 5 Dogleg par 5 Straight par 4 Dogleg par 4 Long par 3 Short par 3
Par 5 5 24 24 3 9
Size 3 3.5 12 15 1 2.25
Enjoyment Index 2 1.5 9 12 1.75 6.75
Construction cost $1,000,000 $1,500,000 $4,500,000 $5,400,000 $600,000 $1,950,000
Number 1 1 6 6 1 3
>= >= >= >= >= >=
1 1 2 2 1 1
Clubhouse
Exclusive
Cost $5,000,000
Size 4
Enjoyment Index 4
Objective Function
Total Enjoyment Index 37
Constraints
Par 5 2 <= 4
Par 4 12 <= 14
Par 3 4 <= 4
Total Size 40.75 <= 42
Total Size 40.75 >= 36
Total Cost $19,950,000 <= $20,000,000
Total Par 70 <= 72
Total Par 70 >= 70
Number of holes 18 = 18
Option 3
In option 3, the project budget is increased to $20.7 million
The model plan
Max ; 2 x1 +1.5 x2 +1.5 x3+2 x4 +1.75 x5+2.25 x6+4z2
Subjects to the constraints
x1 ≥ 1
x2 ≥ 1
x3 ≥ 2
x4 ≥2
x5 ≥ 1
x6 ≥ 1
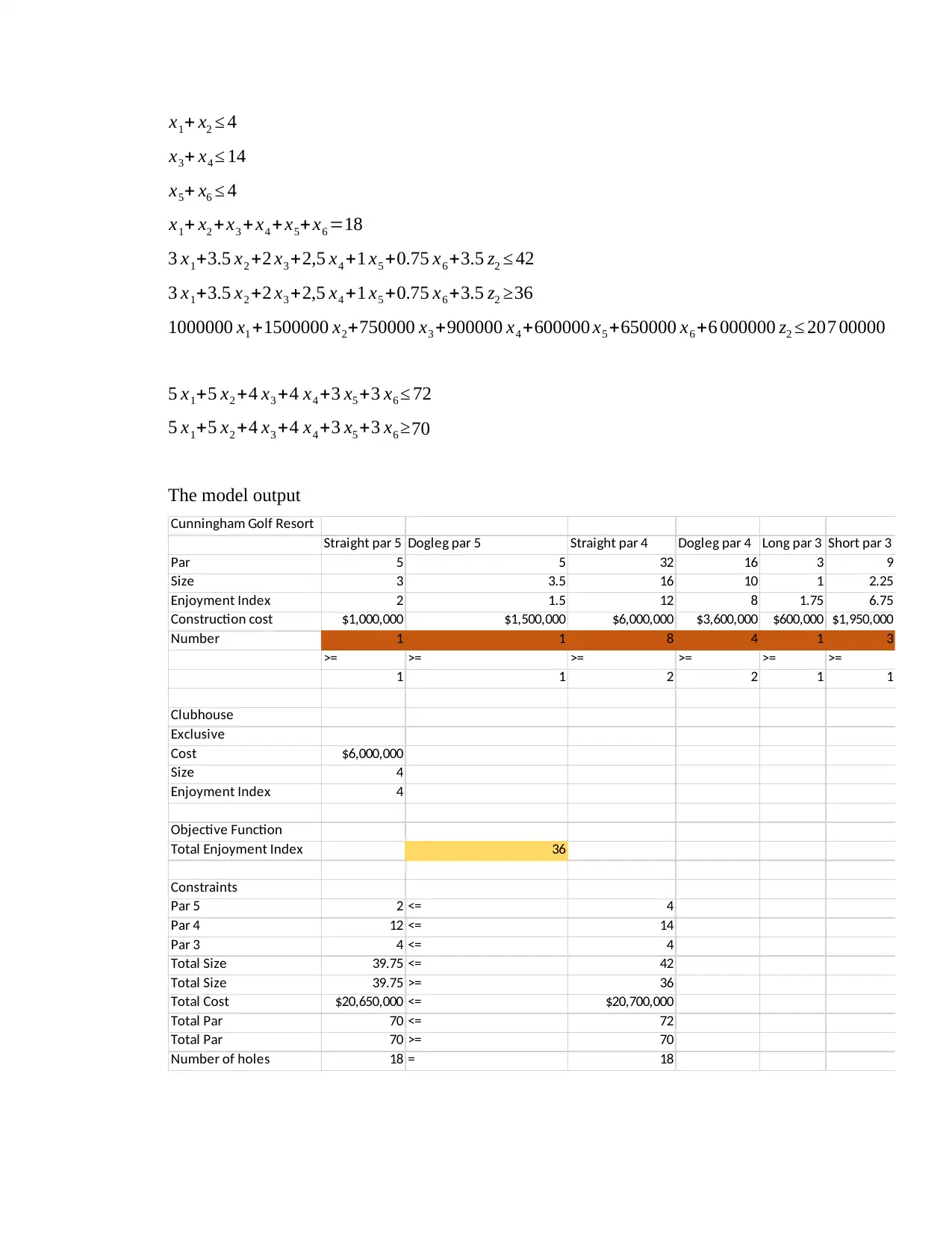
x1+ x2 ≤ 4
x3+ x4 ≤ 14
x5+ x6 ≤ 4
x1+ x2 +x3 + x4 + x5+ x6 =18
3 x1+3.5 x2 +2 x3 +2,5 x4 +1 x5 +0.75 x6 +3.5 z2 ≤ 42
3 x1+3.5 x2 +2 x3 +2,5 x4 +1 x5 +0.75 x6 +3.5 z2 ≥36
1000000 x1 +1500000 x2+750000 x3 +900000 x4 +600000 x5 +650000 x6 +6 000000 z2 ≤ 207 00000
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≤ 72
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≥70
The model output
Cunningham Golf Resort
Straight par 5 Dogleg par 5 Straight par 4 Dogleg par 4 Long par 3 Short par 3
Par 5 5 32 16 3 9
Size 3 3.5 16 10 1 2.25
Enjoyment Index 2 1.5 12 8 1.75 6.75
Construction cost $1,000,000 $1,500,000 $6,000,000 $3,600,000 $600,000 $1,950,000
Number 1 1 8 4 1 3
>= >= >= >= >= >=
1 1 2 2 1 1
Clubhouse
Exclusive
Cost $6,000,000
Size 4
Enjoyment Index 4
Objective Function
Total Enjoyment Index 36
Constraints
Par 5 2 <= 4
Par 4 12 <= 14
Par 3 4 <= 4
Total Size 39.75 <= 42
Total Size 39.75 >= 36
Total Cost $20,650,000 <= $20,700,000
Total Par 70 <= 72
Total Par 70 >= 70
Number of holes 18 = 18
x3+ x4 ≤ 14
x5+ x6 ≤ 4
x1+ x2 +x3 + x4 + x5+ x6 =18
3 x1+3.5 x2 +2 x3 +2,5 x4 +1 x5 +0.75 x6 +3.5 z2 ≤ 42
3 x1+3.5 x2 +2 x3 +2,5 x4 +1 x5 +0.75 x6 +3.5 z2 ≥36
1000000 x1 +1500000 x2+750000 x3 +900000 x4 +600000 x5 +650000 x6 +6 000000 z2 ≤ 207 00000
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≤ 72
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≥70
The model output
Cunningham Golf Resort
Straight par 5 Dogleg par 5 Straight par 4 Dogleg par 4 Long par 3 Short par 3
Par 5 5 32 16 3 9
Size 3 3.5 16 10 1 2.25
Enjoyment Index 2 1.5 12 8 1.75 6.75
Construction cost $1,000,000 $1,500,000 $6,000,000 $3,600,000 $600,000 $1,950,000
Number 1 1 8 4 1 3
>= >= >= >= >= >=
1 1 2 2 1 1
Clubhouse
Exclusive
Cost $6,000,000
Size 4
Enjoyment Index 4
Objective Function
Total Enjoyment Index 36
Constraints
Par 5 2 <= 4
Par 4 12 <= 14
Par 3 4 <= 4
Total Size 39.75 <= 42
Total Size 39.75 >= 36
Total Cost $20,650,000 <= $20,700,000
Total Par 70 <= 72
Total Par 70 >= 70
Number of holes 18 = 18
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

1 out of 10
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





